Inverse problems
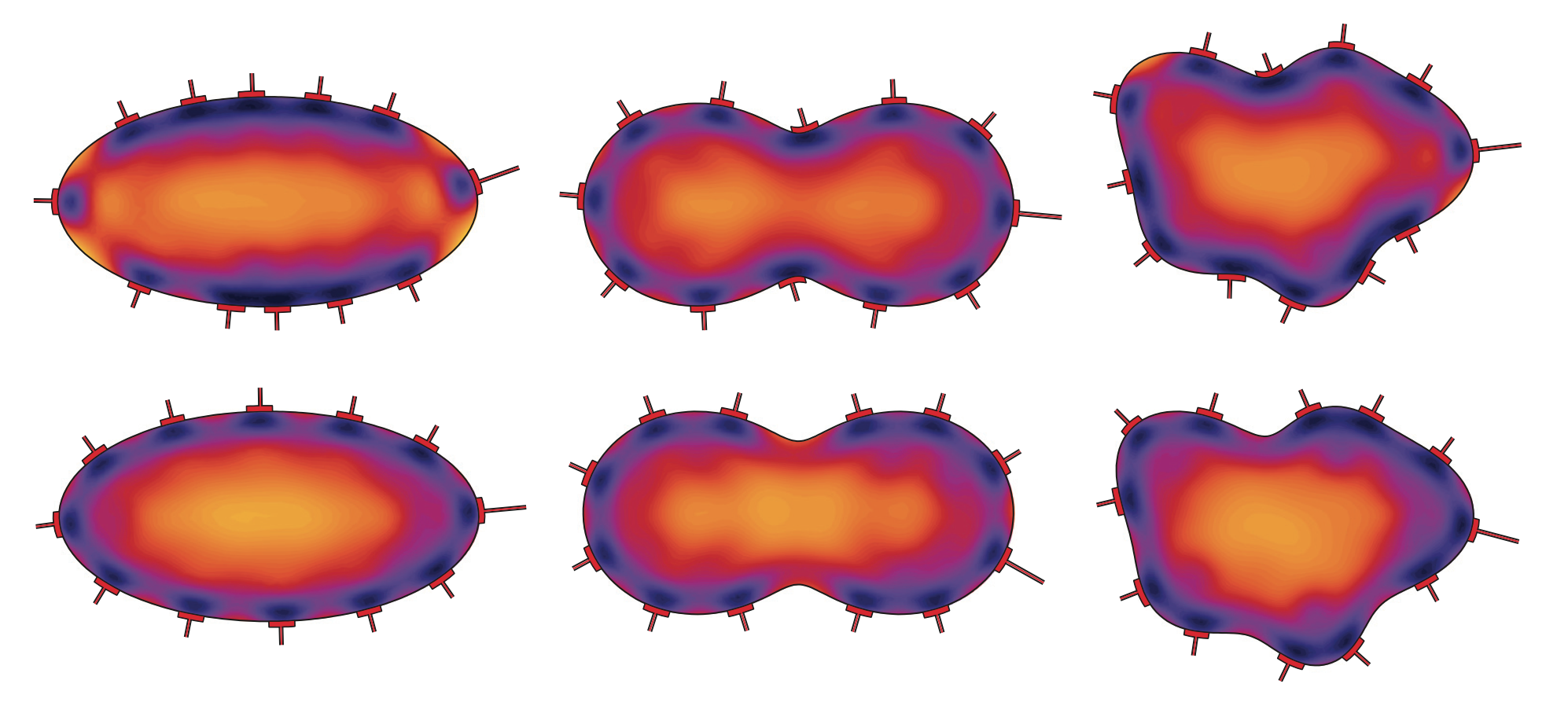
N. Hyvönen, A. Seppänen and S. Staboulis. Optimizing electrode positions in EIT. SIAM Journal on Applied Mathematics 2014, Vol. 74, pp. 1831-1851.
Inverse problems constitute an active and expanding research field of mathematics and its applications. Inverse problems are encountered in several areas of applied sciences such as biomedical engineering and imaging, geosciences, vulcanology, remote sensing, and non-destructive material evaluation. To put it short, a forward problem is to deduce consequences of a cause, while the corresponding inverse problem is to find the causes of a known consequence. Inverse problems are typically encountered when one has indirect observations of the quantity of interest.
A fundamental feature of inverse problems is that they are often ill-posed: Small errors in the measured data can cause arbitrarily large errors in the estimates of the parameters of interest, or can even render the problem unsolvable. It may also occur that an inverse problem does not have a unique solution, i.e., there are several different parameter values that could produce the same observed data. In consequence, to successfully tackle inverse problems, one needs to have comprehensive understanding of the uniqueness and stability of the solution as well as state-of-the-art methods for incorporating prior information into the inverse solver algorithms.
Personnel
Research projects
The group has numerous domestic and international research contacts. Domestic collaboration is organized through the Finnish Inverse Problems Society. The group is affiliated with
Inverse problems link
Publications
Warning this listing of publications might be old, please replace this listing.2021 | 2020 | 2019 | 2018 | 2017 | 2016 | 2015 | 2014 | 2013 | 2012 | 2011 | 2010 | 2009 | 2008 | 2007 | 2006 | 2005 | 2004 | 2003 | 2002 | 1999 | 1997 | 1996 | 1995 | 1994
Giani, Stefano, Hakula, Harri: On effects of perforated domains on parameter-dependent free vibration, Journal of Computational and Applied Mathematics. 394, 2021. [BibTeX...]
Giani, Stefano, Grubišić, Luka, Hakula, Harri, Ovall, Jeffrey S.: A Posteriori Error Estimates for Elliptic Eigenvalue Problems Using Auxiliary Subspace Techniques, JOURNAL OF SCIENTIFIC COMPUTING. 88(3), 2021. [BibTeX...]
Burger, M., Hauptmann, A., Helin, T., Hyvönen, N., Puska, J. P.: Sequentially optimized projections in x-ray imaging, Inverse Problems. 37(7), 2021. [BibTeX...]
Hannukainen, Antti, Hyvonen, Nuutti, Perkkiö, Lauri: Inverse heat source problem and experimental design for determining iron loss distribution, SIAM JOURNAL ON SCIENTIFIC COMPUTING. 43(2), 2021, p. B243-B270. [BibTeX...]
Garde, Henrik, Hyvonen, Nuutti: Mimicking relative continuum measurements by electrode data in two-dimensional electrical impedance tomography, Numerische Mathematik., 2021. [BibTeX...]
Candiani, Valentina, Darde, Jeremie, Garde, Henrik, Hyvönen, Nuutti: Monotonicity-Based Reconstruction of Extreme Inclusions in Electrical Impedance Tomography, SIAM JOURNAL ON MATHEMATICAL ANALYSIS. 52(6), 2020, p. 6234–6259. [BibTeX...]
Hakula, Harri: Adaptive reference elements via harmonic extensions and associated inner modes, COMPUTERS AND MATHEMATICS WITH APPLICATIONS. 80(11), 2020, p. 2272-2288. [BibTeX...]
Butler, Troy, Hakula, Harri: What do we hear from a drum? A data-consistent approach to quantifying irreducible uncertainty on model inputs by extracting information from correlated model output data, Computer Methods in Applied Mechanics and Engineering. 370, 2020. [BibTeX...]
Giani, Stefano, Hakula, Harri: On effective material parameters of thin perforated shells under static loading, Computer Methods in Applied Mechanics and Engineering. 367, 2020. [BibTeX...]
Garde, Henrik, Hyvönen, Nuutti, Kuutela, Topi: On regularity of the logarithmic forward map of electrical impedance tomography, SIAM JOURNAL ON MATHEMATICAL ANALYSIS. 52(1), 2020, p. 197–220. [BibTeX...]
Garde, Henrik, Hyvönen, Nuutti: Optimal depth-dependent distinguishability bounds for electrical impedance tomography in arbitrary dimension, SIAM Journal on Applied Mathematics. 80(1), 2020, p. 20-43. [BibTeX...]
Hakula, Harri, Laaksonen, Mikael: Frequency response analysis of perforated shells with uncertain materials and damage, APPLIED SCIENCES. 9(24), 2019, p. 1-22. [BibTeX...]
Bezrodnykh, Sergei, Bogatyrëv, Andrei, Goreinov, Sergei, Grigor'ev, Oleg, Hakula, Harri, Vuorinen, Matti: On capacity computation for symmetric polygonal condensers, Journal of Computational and Applied Mathematics. 361, 2019, p. 271-282. [BibTeX...]
Babuska, Ivo, Hakula, Harri: Pointwise error estimate of the Legendre expansion The known and unknown features, Computer Methods in Applied Mechanics and Engineering. 345, 2019, p. 748-773. [BibTeX...]
Hannukainen, Antti, Hyvönen, Nuutti, Mustonen, Lauri: An inverse boundary value problem for the p-Laplacian A linearization approach, Inverse Problems. 35(3), 2019. [BibTeX...]
Candiani, Valentina, Hannukainen, Antti, Hyvonen, Nuutti: Computational framework for applying electrical impedance tomography to head imaging, SIAM JOURNAL ON SCIENTIFIC COMPUTING. 41(5), 2019, p. B1034-B1060. [BibTeX...]
Laaksonen, Mikael, Hakula, Harri: Multiparametric shell eigenvalue problems, Computer Methods in Applied Mechanics and Engineering. 343, 2019, p. 721-745. [BibTeX...]
Hakula, Harri, Laaksonen, Mikael: Asymptotic convergence of spectral inverse iterations for stochastic eigenvalue problems, Numerische Mathematik. 142(3), 2019, p. 577-609. [BibTeX...]
Hakula, Harri, Quach, Tri, Rasila, Antti: The Conjugate Function Method and Conformal Mappings in Multiply Connected Domains, SIAM JOURNAL ON SCIENTIFIC COMPUTING. 41(3), 2019, p. A1753-A1776. [BibTeX...]
Laaksonen, Mikael, Hakula, Harri, Kaarnioja, Vesa: Cylindrical Shell with Junctions: Uncertainty Quantification of Free Vibration and Frequency Response Analysis, Shock and Vibration. 2018, 2018. [BibTeX...]
Hyvönen, Nuutti, Mustonen, Lauri: Generalized linearization techniques in electrical impedance tomography, Numerische Mathematik. 140(1), 2018, p. 95-120. [BibTeX...]
Hyvönen, Nuutti, Päivärinta, Lassi, Tamminen, Janne: Enhancing D-bar reconstructions for electrical impedance tomography with conformal maps, INVERSE PROBLEMS AND IMAGING. 12(2), 2018, p. 373-400. [BibTeX...]
Giani, Stefano, Grubisic, Luka, Hakula, Harri, Ovall, Jeffrey S.: An a posteriori estimator of eigenvalue/eigenvector error for penalty-type discontinuous Galerkin methods, APPLIED MATHEMATICS AND COMPUTATION. 319, 2018, p. 562-574. [BibTeX...]
Shah, Sahas Bikram, Rasilo, Paavo, Hakula, Harri, Arkkio, Antero: Efficient finite element method to estimate eddy current loss due to random interlaminar contacts in electrical sheets, INTERNATIONAL JOURNAL OF NUMERICAL MODELLING: ELECTRONIC NETWORKS DEVICES AND FIELDS. 31(4), 2018. [BibTeX...]
Hyvönen, Nuutti, Mustonen, Lauri: Thermal tomography with unknown boundary, SIAM JOURNAL ON SCIENTIFIC COMPUTING. 40(3), 2018, p. B662-B683. [BibTeX...]
Hakula, Harri, Rasila, Antti, Vuorinen, Matti: Conformal modulus and planar domains with strong singularities and cusps, Electronic Transactions on Numerical Analysis. 48, 2018, p. 462-478. [BibTeX...]
G., David Gonzalez, Hakula, Harri, Rasila, Antti, Hamalainen, Jyri: Spatial Mappings for Planning and Optimization of Cellular Networks, IEEE-ACM TRANSACTIONS ON NETWORKING. 26(1), 2018, p. 175-188. [BibTeX...]
Hyvönen, Nuutti, Mustonen, Lauri: Smoothened complete electrode model, SIAM Journal on Applied Mathematics. 77(6), 2017, p. 2250–2271. [BibTeX...]
Gustafsson, Tom, Hakula, Harri, Leinonen, Matti: Stochastic Galerkin approximation of the Reynolds equation with irregular film thickness, COMPUTERS AND MATHEMATICS WITH APPLICATIONS. 74(7), 2017, p. 1590-1606. [BibTeX...]
Barth, Andrea, Harrach, Bastian, Hyvönen, Nuutti, Mustonen, Lauri: Detecting stochastic inclusions in electrical impedance tomography, Inverse Problems. 33(11), 2017, p. 1-18. [BibTeX...]
Hakula, Harri, Neilan, Michael, Ovall, Jeffrey S.: A Posteriori Estimates Using Auxiliary Subspace Techniques, JOURNAL OF SCIENTIFIC COMPUTING. 72(1), 2017, p. 97-127. [BibTeX...]
Hyvönen, N., Majander, H., Staboulis, S.: Compensation for geometric modeling errors by positioning of electrodes in electrical impedance tomography, Inverse Problems. 33(3), 2017. [BibTeX...]
Hyvönen, N., Kaarnioja, V., Mustonen, L., Staboulis, S.: Polynomial collocation for handling an inaccurately known measurement configuration in electrical impedance tomography, SIAM Journal on Applied Mathematics. 77(1), 2017, p. 202-223. [BibTeX...]
Hannukainen, A., Hyvönen, N., Majander, H., Tarvainen, T.: Efficient inclusion of total variation type priors in quantitative photoacoustic tomography, SIAM JOURNAL ON IMAGING SCIENCES. 9(3), 2016, p. 1132-1153. [BibTeX...]
Hannukainen, A., Harhanen, L., Hyvönen, N., Majander, H.: Edge-promoting reconstruction of absorption and diffusivity in optical tomography, Inverse Problems. 32(1), 2016. [BibTeX...]
Hyvönen, Nuutti, Leinonen, Matti: Stochastic Galerkin finite element method with local conductivity basis for electrical impedance tomography, SIAM/ASA Journal on Uncertainty Quantification. 3(1), 2015, p. 998-1019. [BibTeX...]
Harhanen, Lauri, Hyvönen, Nuutti, Majander, Helle, Staboulis, Stratos: Edge-enhancing reconstruction algorithm for three-dimensional electrical impedance tomography, SIAM JOURNAL ON SCIENTIFIC COMPUTING. 37(1), 2015, p. B60-B78. [BibTeX...]
Hame, Lauri, Hakula, Harri: A Maximum Cluster Algorithm for Checking the Feasibility of Dial-A-Ride Instances, TRANSPORTATION SCIENCE. 49(2), 2015, p. 295-310. [BibTeX...]
Hakula, H., Kaarnioja, V., Laaksonen, M.: Approximate methods for stochastic eigenvalue problems, APPLIED MATHEMATICS AND COMPUTATION.(267), 2015, p. 664-681. [BibTeX...]
Hakula, Harri, Laaksonen, Mikael: Hybrid Stochastic Finite Element Method for Mechanical Vibration Problems, Shock and Vibration.(2015), 2015, p. 812069. [BibTeX...]
Chesnel, Lucas, Hyvönen, Nuutti, Staboulis, Stratos: Construction of invisible conductivity perturbations for the point electrode model in electrical impedance tomography, SIAM Journal on Applied Mathematics. 75(5), 2015, p. 2093-2109. [BibTeX...]
Leinonen, Matti, Hakula, Harri, Hyvonen, Nuutti: Application of stochastic Galerkin FEM to the complete electrode model of electrical impedance tomography, JOURNAL OF COMPUTATIONAL PHYSICS. 269(1), 2014, p. 181-200. [BibTeX...]
Kettunen, Henrik, Chesnel, Lucas, Hakula, Harri, Wallén, Henrik, Sihvola, Ari: Surface plasmon resonances on cones and wedges, 8th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics (Metamaterials 2014), Copenhagen, Denmark, 24-30 August 2014., p. 163-165. [BibTeX...]
Hyvönen, Nuutti, Seppänen, Aku, Staboulis, Stratos: Optimizing electrode positions in electrical impedance tomography, SIAM Journal on Applied Mathematics. 74(6), 2014, p. 1831-1851. [BibTeX...]
Hakula, Harri, Hyvönen, Nuutti, Leinonen, Matti: Reconstruction algorithm based on stochastic Galerkin finite element method for electrical impedance tomography, Inverse Problems. 30(6), 2014, p. 065006. [BibTeX...]
Hakula, Harri: hp-boundary layer mesh sequences with applications to shell problems, COMPUTERS AND MATHEMATICS WITH APPLICATIONS. 67(4), 2014, p. 899-917. [BibTeX...]
Hakula, Harri, Tuominen, Tomi: On hp-adaptive solution of thin shells of revolution, IOP CONFERENCE SERIES: MATERIALS SCIENCE AND ENGINEERING. 10(1), 2014. [BibTeX...]
Hakula, Harri, Tuominen, Tomi: Mathematica implementation of the high order finite element method applied to eigenproblems, COMPUTING: ARCHIVES FOR SCIENTIFIC COMPUTING. 95(SUPPL.1), 2013. [BibTeX...]
Häme, Lauri, Hakula, Harri: Dynamic journeying under uncertainty, EUROPEAN JOURNAL OF OPERATIONAL RESEARCH. 225(3), 2013, p. 455-471. [BibTeX...]
Häme, Lauri, Hakula, Harri: Routing by ranking A link analysis method for the constrained dial-A-ride problem, Operations Research Letters. 41(6), 2013, p. 664-669. [BibTeX...]
Hyvönen, Nuutti, Nandakumaran, Akambadath K., Varma, Hari M., Vasu, Ram M.: Generalized eigenvalue decomposition of the field autocorrelation in correlation diffusion of photons in turbid media, MATHEMATICAL METHODS IN THE APPLIED SCIENCES. 36(11), 2013, p. 1447-1458. [BibTeX...]
Hame, Lauri, Hakula, Harri: Dynamic journeying in scheduled networks, IEEE TRANSACTIONS ON INTELLIGENT TRANSPORTATION SYSTEMS. 14(1), 2013, p. 360-369. [BibTeX...]
Hakula, Harri, Rasila, Antti, Vuorinen, Matti: Computation of exterior moduli of quadrilaterals, Electronic Transactions on Numerical Analysis.(40), 2013, p. 436-451. [BibTeX...]
Griesmaier, Roland, Hyvönen, Nuutti, Seiskari, Otto: A note on analyticity properties of far field patterns, INVERSE PROBLEMS AND IMAGING. 7(2), 2013, p. 491-498. [BibTeX...]
Darde, Jeremi, Hyvönen, Nuutti, Seppänen, Aku, Staboulis, Stratos: Simultaneous recovery of admittivity and body shape in electrical impedance tomography: An experimental evaluation, Inverse Problems. 29(8), 2013. [BibTeX...]
Darde, Jeremi, Hyvönen, Nuutti, Seppänen, Aku, Staboulis, Stratos: Simultaneous reconstruction of outer boundary shape and admittivity distribution in electrical impedance tomography, SIAM JOURNAL ON IMAGING SCIENCES. 6(1), 2013, p. 176-198. [BibTeX...]
Darde, Jeremi, Hannukainen, Antti, Hyvönen, Nuutti: An Hdiv-based mixed quasi-reversibility method for solving elliptic Cauchy problems, SIAM JOURNAL ON NUMERICAL ANALYSIS. 51(4), 2013, p. 2123-2148. [BibTeX...]
Hanke, Martin, Harhanen, Lauri, Hyvönen, Nuutti, Schweickert, Eva: Convex source support in three dimensions, BIT NUMERICAL MATHEMATICS. 52(1), 2012, p. 45-63. [BibTeX...]
Hyvönen, Nuutti, Seiskari, Otto: Detection of multiple inclusions from sweep data of electrical impedance tomography, Inverse Problems.(28), 2012. [BibTeX...]
Hyvönen, Nuutti, Piiroinen, Petteri, Seiskari, Otto: Point measurements for a Neumann-to-Dirichlet map and the Calderon problem in the plane, SIAM JOURNAL ON MATHEMATICAL ANALYSIS. 44(5), 2012, p. 3526-3536. [BibTeX...]
Hakula, Harri, Quach, Tri, Rasila, Antti: Conjugate function method for numerical conformal mappings, Journal of Computational and Applied Mathematics.(237), 2012, p. 340-353. [BibTeX...]
Hakula, Harri, Hyvönen, Nuutti, Tuominen, Toni: On the hp-adaptive solution of complete electrode model forward problems of electrical impedance tomography, Journal of Computational and Applied Mathematics. 236(236), 2012, p. 4645-4659. [BibTeX...]
Darde, Jeremi, Hakula, Harri, Hyvönen, Nuutti, Staboulis, Stratos: Fine-tuning electrode information in electrical impedance tomography, INVERSE PROBLEMS AND IMAGING. 6(6), 2012, p. 399-421. [BibTeX...]
Varma, Hari M, Mohanan, Kuriyakkatil P., Hyvönen, Nuutti, Nandakumaran, Akambadath K., Vasu, Ram M.: Ultrasound-modulated optical tomography: recovery of amplitude of vibration in the insonified region from boundary measurement of light correlation, JOURNAL OF THE OPTICAL SOCIETY OF AMERICA A: OPTICS IMAGE SCIENCE AND VISION. 28, 2011, p. 2322-2332. [BibTeX...]
Häme, Lauri, Hyytiä, Esa, Hakula, Harri: The Traveling Salesman Problem with Differential Neighborhoods, The 27th European Workshop on Computational Geometry (EuroCG) , March 28-30, 2011, Antoniushaus Morschach, Switzerland.., p. 51-54. [BibTeX...]
Havola, Linda, Majander, Helle, Hakula, Harri, Alestalo, Pekka, Rasila, Antti: Aktivoiviin opetusmenetelmiin perustuvat matematiikan opetuskokeilut Aalto-yliopistossa, Tuovi 9: Interaktiivinen tekniikka koulutuksessa 2011 -konferenssin tutkijatapaamisen artikkelit., p. 5-9. [BibTeX...]
Hanke, Martin, Hyvönen, Nuutti, Reusswig, Stefanie: Erratum: An inverse backscatter problem for electric impedance tomography, SIAM JOURNAL ON MATHEMATICAL ANALYSIS. 43(3), 2011, p. 1495-1497. [BibTeX...]
Hanke, Martin, Hyvönen, Nuutti, Reusswig, Stefanie: Convex backscattering support in electric impedance tomography, Numerische Mathematik. 117(2), 2011, p. 373-396. [BibTeX...]
Hanke, Martin, Harrach, Bastian, Hyvönen, Nuutti: Justification of point electrode models in electrical impedance tomography, Mathematical Models and Methods in Applied Sciences. 21, 2011, p. 13951413. [BibTeX...]
Hakula, Harri, Harhanen, Lauri, Hyvönen, Nuutti: Sweep data of electrical impedance tomography, Inverse Problems. 27(11), 2011, p. 115006. [BibTeX...]
Hakula, Harri, Rasila, Antti, Vuorinen, Matti: On Moduli of Rings and Quadrilaterals: Algorithms and Experiments, SIAM JOURNAL ON SCIENTIFIC COMPUTING. 33(1), 2011, p. 279-302. [BibTeX...]
Griesmaier, R, Hyvönen, Nuutti: A regularized Newton method for locating thin tubular conductivity inhomogeneities, Inverse Problems. 27, 2011. [BibTeX...]
Hyvönen, Nuutti, Karhunen, Kimmo, Seppänen, Aku: Frechet derivative with respect to the shape of an internal electrode in electrical impedance tomography, SIAM Journal on Applied Mathematics. 70(6), 2010, p. 1878-1898. [BibTeX...]
Hyvönen, Nuutti, Kalke, M., Lassas, Matti, Setälä, H.: Three-dimensional dental X-ray imaging by combination of panoramic and projection data, INVERSE PROBLEMS AND IMAGING. 4(2), 2010, p. 257-271. [BibTeX...]
Harhanen, Lauri, Hyvönen, Nuutti: Convex source support in half-plane, INVERSE PROBLEMS AND IMAGING. 4(3), 2010, p. 429-448. [BibTeX...]
Hyvönen, Nuutti: Approximating idealized boundary data of electric impedance tomography by electrode measurements, Mathematical Models and Methods in Applied Sciences. 19, 2009, p. 1185-1202. [BibTeX...]
Hyvönen, Nuutti: An inverse backscatter problem for electric impedance tomography, SIAM JOURNAL ON MATHEMATICAL ANALYSIS. 41, 2009, p. 1948-1966. [BibTeX...]
Hyvönen, Nuutti: Comparison of idealized and electrode Dirichlet-to-Neumann maps in electric impedance tomography with an application to boundary determination of conductivity, Inverse Problems. 25, 2009. [BibTeX...]
Hakula, Harri, Hyvönen, Nuutti: On computation of test dipoles for factorization method, BIT. 49, 2009, p. 75-91. [BibTeX...]
Hakula, Harri, Rasila, Antti, Vuorinen, Matti: On moduli of rings and quadrilaterals: algorithms and experiments, 2009. [BibTeX...]
Calvetti, Daniela, Hakula, Harri, Pursiainen, Sampsa, Somersalo, Erkki: Conditionally Gaussian Hypermodels for Cerebral Source Localization, SIAM JOURNAL ON IMAGING SCIENCES. 2(3), 2009, p. 879-909. [BibTeX...]
Artioli, Edoardo, Beirao da Veiga, Lourenco, Hakula, Harri, Lovadina, Carlo: On the asymptotic behaviour of shells of revolution in free vibration, COMPUTATIONAL MECHANICS. 44(1), 2009, p. 45-60. [BibTeX...]
Niemi, Antti H., Pitkäranta, Juhani, Hakula, Harri: Point load on a shell, Numerical mathematics and advanced applications., p. 819-826. [BibTeX...]
Lechleiter, A., Hyvönen, Nuutti, Hakula, Harri: The factorization method applied to the complete electrode model of impedance tomography, SIAM Journal on Applied Mathematics. 68(4), 2008, p. 1097-1121. [BibTeX...]
Hanke, M., Hyvönen, Nuutti, Reusswig, R.: Convex source support and its application to electric impedance tomography, SIAM JOURNAL ON IMAGING SCIENCES. 1(4), 2008, p. 364-378. [BibTeX...]
Hanke, Martin, Hyvonen, Nuutti, Lehn, Manfred, Reusswig, Stefanie: Source supports in electrostatics, BIT NUMERICAL MATHEMATICS. 48(2), 2008, p. 245-264. [BibTeX...]
Hakula, Harri, Hyvonen, Nuutti: Two noniterative algorithms for locating inclusions using one electrode measurement of electric impedance tomography, Inverse Problems. 24(5), 2008, p. 055018. [BibTeX...]
Gebauer, Bastian, Hyvonen, Nuutti: Factorization method and inclusions of mixed type in an inverse elliptic boundary value problem, INVERSE PROBLEMS AND IMAGING. 2(3), 2008, p. 355-372. [BibTeX...]
Calvetti, Daniela, Hakula, Harri, Pursiainen, Sampsa, Somersalo, Erkki: Conditionally Gaussian hypermodels for source localization in brain imaging, arXiv.org., 2008. [BibTeX...]
Artioli, Edoardo, de Veiga, Lourenco Beirao, Hakula, Harri, Lovadina, Carlo: Free vibrations for some Koiter shells of revolution, APPLIED MATHEMATICS LETTERS. 21(12), 2008, p. 1245-1248. [BibTeX...]
Niemi, Antti H., Pitkäranta, Juhani, Hakula, Harri: Benchmark computations on point-loaded shallow shells: Fourier vs.FEM, Computer Methods in Applied Mechanics and Engineering. 196(4-6), 2007, p. 894-907. [BibTeX...]
Hyvönen, Nuutti: Application of the factorization method to the characterization of weak inclusions in electrical impedance tomography, ADVANCES IN APPLIED MATHEMATICS. 39(2), 2007, p. 197-221. [BibTeX...]
Hyvönen, Nuutti, Hakula, Harri, Pursiainen, Sampsa: Numerical implementation of the factorization method within the complete electrode model of electrical impedance tomography, INVERSE PROBLEMS AND IMAGING. 1(2), 2007, p. 299-317. [BibTeX...]
Hyvönen, Nuutti: Locating Transparent Regions in Optical Absorption and Scattering Tomography, SIAM Journal on Applied Mathematics. 67, 2007, p. 1101-1123. [BibTeX...]
Hyvönen, Nuutti: Frechet derivative with respect to the shape of a strongly convex nonscattering region in optical tomography, Inverse Problems. 23, 2007, p. 2249-2270. [BibTeX...]
Hyvönen, Nuutti: Locating transparent cavities in optical absorption and scattering tomography, Workshop: Inverse problems in wave scattering organised by Mathematisches Forschungsinstitut Oberwolfach, March 4-10, 2007.. [BibTeX...]
Gebauer, B., Hyvönen, Nuutti: Factorization method and irregular inclusions in electrical impedance tomography, Inverse Problems. 23, 2007, p. 2159-2170. [BibTeX...]
Pursiainen, Sampsa, Hakula, Harri: A High-order Finite Element Method for Electical Impedance Tomography, PIERS Online. 2(3), 2006, p. 260-264. [BibTeX...]
Niemi, Antti, Pitkäranta, Juhani, Hakula, Harri: A benchmark study: MITC4-S and boundary layer-type deformations, Rakenteiden mekaniikka. 38, 2005, p. 71-74. [BibTeX...]
Hyvönen, Nuutti: Application of a weaker formulation of the factorization method to the characterization of absorbing inclusions in optical tomography, Inverse Problems. 21, 2005, p. 1331-1342. [BibTeX...]
Hyvönen, Nuutti: Complete electrode model of electrical impedance tomography: Approximation properties and characterization of inclusions, SIAM Journal on Applied Mathematics. 64, 2004, p. 902-931. [BibTeX...]
Hyvönen, Nuutti: Diffusive tomography methods: special boundary conditions and characterization of inclusions, 2004. [BibTeX...]
Hyvönen, Nuutti: Characterizing inclusions in optical tomography, Inverse Problems. 20, 2004, p. 737-751. [BibTeX...]
Havu, Ville, Hakula, Harri: On sensitive shell under different loadings, 4th European Congress on Computational Methods in Applied Sciences and Engineering, ECCOMAS 2004, Jyväskylä, 2004.. [BibTeX...]
Havu, Ville, Hakula, Harri, Tuominen, Tomi: A benchmark study of elliptic and hyperbolic shells of revolution, 2003. [BibTeX...]
Havu, Ville, Hakula, Harri: MITC4-kuorielementin konvergenssiominaisuudet, VIII Suomen mekaniikkapäivät, Espoo 12.-13.6.2003., p. 533-539. [BibTeX...]
Pitkäranta, Juhani, Hakula, Harri, Havu, Ville, Malinen, Mika: Convergence of the MITC4 Shell Element, The Fifth World Congress on Computational Mechanics (WCCM V), July 7-12, Vienna, Austria.. [BibTeX...]
Hyvönen, Nuutti: Analysis of optical tomography with non-scattering regions, Proceedings of the Edinburgh Mathematical Society. 45, 2002, p. 257-276. [BibTeX...]
Hakula, H.: Controlling 2D Voronoi-Segment Methods, 8th International Mesh Generation Roundtable, October 10-13,South Lake Tahoe, California., p. 221-229. [BibTeX...]
Hakula, H.: High-Order Finite Element Tools for Shell Problems, 1997. [BibTeX...]
Hakula, H., Pitkäranta, J.: Pinched shells of revolution: experiments on high order FEM, ICOSAHOM.95, Houston, Texas, 5-9 June 1995., p. 193-201. [BibTeX...]
Hakula, H., Leino, Y., Pitkäranta, J.: Scale resolution locking, and high-order finite element modelling of shells, Computer Methods in Applied Mechanics and Engineering. 133, 1996, p. 157-182. [BibTeX...]
Hakula, H.: Low-Dispersion Meshes for Scattering Problems, 5th International Conference on Numerical Grid Generation in Computational Field Simulations., p. 639-645. [BibTeX...]
Hakula, H., Pitkäranta, J.: Pinched Shells of Revolution: Experiments on High Order FEM, 1995. [BibTeX...]
Hakula, H., Leino, Y., Pitkäranta, J.: Scale Resolution, Locking, and High-Order Finite Element Modelling of Shells, 1995. [BibTeX...]
Hakula, H.: Generating meshes for scales in shells, Numerical Grid Generation in CFD and Related Fields, Swansea, March 1994., p. 177-186. [BibTeX...]
Hakula, H., Malinen, Jarmo, Kallberg, P., Valve, P.: The finite element method applied to the exterior Helmholtz problem on the IBM SP1, Para 94, Kööpenhamina, 20-23 kesäkuu 1994., p. 262-269. [BibTeX...]
To the top
Page content by: webmaster-math [at] list [dot] aalto [dot] fi




