MATLAB-perusteet
MATLAB on interaktiivinen vektori- ja matriisilaskentaohjelmisto. Se on matriisikieli, joka soveltuu mitä moninaisimpiin tieteellisen ja teknisen laskennan tehtäviin.
Cleve Moler kirjoitti alkuperäisen MATLAB:in Fortran-version vuonna 1978 matriisilaskennan helppokäyttöiseksi opettelu- ja kokeiluympäristöksi, "matriisilaskimeksi". Esikuvana kielelle voidaan pitää Kenneth Iversonin 1960-luvulla kehittämää APL-kieltä.
Cleve Moler kirjoitti Fortran-kielellä matriisitulkin, joka käytti LINPACK- ja EISPACK- kirjastojen rutiineja laskentakoneenaan. Matlab:n ytimenä on edelleen numeerisen lineaarialgebran "peruskallion" muodostama Fortran-ohjelmakokoelma, joka kehittyi edellä mainittujen kahden kirjaston yhdistämisenä ja päivityksenä. Tämä Fortran90-kielellä kirjoitettu kirjasto on nimeltään LAPACK.
Matlabin lyhyt historia
Cleve Moler: A Brief History of MATLABAlkuperäinen MATLAB oli julkisohjelma, jota levitettiin yliopistoille. Nykyversiot (vuodesta 1984 lähtien) ovat C-kielellä kirjoitettuja, The MathWorks Inc.:n toimittamia kaupallisia tuotteita, joihin on tehty lukuisia laajennuksia alkuperäiseen MATLAB-ohjelmaan verrattuna. Toisaalta vanhojen koodioen yhteensopivuus uusissa ohjelmaversioissa on säilnyt erittäin hyvin. Ohjelmakoodit myös avautuvat ongelmitta, koska ne talletetaan tavallisina tekstitiedostoina. (Tämän oppaan kirjoittajan ensimmäiset Matlab-koodit ovat 1980-luvun alkuvuosilta Fortranilla kirjoitetulle Matlabille tehtyjä, ja toimivat edelleen.)
Kaupalliset lisenssit ovat varsin arvokkaita, mutta mm. opiskelutarkoituksiin on saatavissa/neuvoteltavissa edullisia lisenssejä. Lisäksi Matlab:n käytön opettelussa voi käyttää julkisohjelmia Octave tai Scilab, joista edellinen on suoremmin yhteensopiva, mutta jälkimmäsen kieli on myös kutakuinkin uskollinen MATLAB:lle, ja sisältää konversio-työkalut epäyhteensopivuuksien hoitamiseksi.
MATLABin hyviä puolia:
**Tähän tehokkuusasiaa, tulkkaus hidastaa, parannuskeinoja:
- Helppo interaktiivinen käyttö mahdollistaa nopean kehittelyn ja virheiden jäljityksen.
- Matriisilaskennalle luonteenomainen korkean tason kieli.
- Matlab-ohjelmien siirrettävyys eri koneiden välillä ongelmatonta.
- Vanhojen koodien yhteensopivuus uusiin versioihin.
- Kehittäjinä parhaat numeeristen menetelmien asiantuntijat
- Laaja (alati laajeneva) joukko valmiita funktioita ja 'toolboxeja'.
- Suuri määrä laajan käyttäjäkunnan tarjoamia ilmaisia koodeja.
** Tarkenna hiukan kts. Hig-HIG s. xxi**
- Vektorointi
- Kääntäminen
- Mex-mekanismi: Eri kielisten ohjelmien kutsuminen
- Parallel toolbox
Käyttösuosituksia, avustusta, help,doc
Muista aina tämä, jo etusivulla mainittu: https://se.mathworks.com/help/matlab/
Jos haluat mennä suoraan aiheesen "elementary math with Matlab",
klikkaa tätä: https://se.mathworks.com/help/matlab/elementary-math.html
MATLAB:ssa ja OCTAVE:ssa kattavat avustustoiminnot.
Komennot >> help, >> doc ja käyttöliittymän ikkunan [?] johdattavat avustuksen jäljille, ja niihin pääsee käsiksi myös suoraan www-linkeistä, kuten yllä.** PARANTELE ja selkiytä ***
tai kirjoittamalla selainikkunaan "Matlab [hakusana]", "Octave [hakusana]".
Kokeile vaikka: matlab functions , octave help .HUOM: Oppaamme tekstissä esiintyvät linkkisanat (Matlab-funktionimet) ovat linkkejä MATLAB:n/OCTAVE:n komentojen
help [nimi] ja doc [nimi] antamiin dokumentteihin.Käsillä on interaktiivisen ohjelman interaktiivinen käyttöopas. Siispä kannattaa pitää MATLAB/OCTAVE-istunto auki ja suorittaa tekstissä esiintyviä (ja omiakin) komentoja. Osassa istuntoesimekkejä annetaan vain käyttäjän antamat komennot ilman tulostuksia. Tämä selkeyttää ja lyhentää tekstiä ja motivoi paremmin lukijaa omatoimiseen kokeiluun ohjelmalla. Huomaa, että oppaan sivulta voi suoraan leikata/liimata istuntojen osia MATLABiin.
MATLAB Windows-, Macintosh- ja Unix/Linux- ympäristöissä
Uusin (6.8.2019) kokeilemani versio on 2019a, versiot ovat vauhdilla kasvava luonnonvara. Lähes kaikki oppaan alkuosan opit pätevät miltei ensimmäisistä ohjelman versiosta alkaen. Vuoden 1997 versiossa tulivat mukaan mm. moniulotteiset taulukot, solutaulukot ("cell arrays"), struktuurit ("struct"), harvojen matriisien tietorakenne ("sparse") sekä oliopohjainen ohjelmointi. Käyttöliittymässä on myös tapahtunut huomattavaa kehitystä, uusimman julkaisukelpoisen ja "elävän" dokumentin tuottamiseen on kehitetty ns."LIVE script", josta tuonnempana.
Varsin pitkälle päästään ilman näitä "uusia" rakenteitakin, toki niitä otetaan käyttöön soveltuvin osin pitemmälle edetessämme.
Matlab käynnistyy MATLAB-ikonista tai myös LINUX/UNIX-koneen komentoikkunassa komennolla: matlab&
Tällöin aukeaa alla olevan kuvan mukainen käyttöliittymä, jonka ulkoasua voi säädellä ylhäällä oikealla puolella olevasta "Layout"-ikonista. Keskellä näkyvään komentoikkunaan ("command window") voidaan kirjoittaa komentoja, kuten kuvassa on tehty.
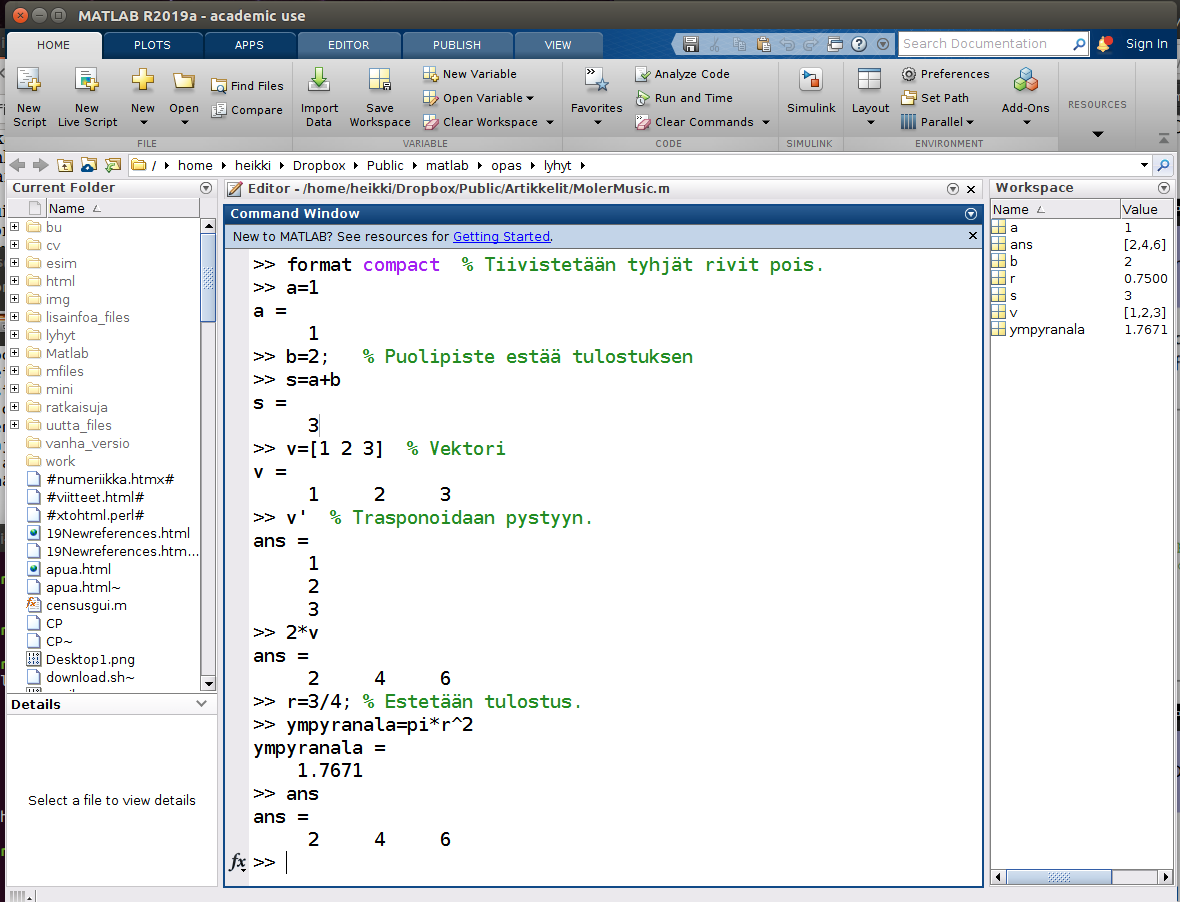
Tässä istunnossa ainoa lisäselvitystä vaativa lienee erikoismuuttuja ans, johon tallentuu edellinen tulos, jota ei ole talletettu muuttujaan. Siksi sen arvo tässä on seuraavien (sijoitus)komentojen jälkeen säilynyt muuttumattomana.
Octave:n käyttöliittymä on vaatimattomampi. Yleensä siinä on editori- ja komentoikkunat, ja sen asua voidaan myös säädellä Etuna Octavessa on nopeampi käynnistys ja myös yksinkertaisemman "ikkunaston" helpompi hallinta.
MATLAB:n hieno käyttöliittymä editorin tarjoamine apuineen on toki erinomaisen hyödyllinen.OCTAVE:n ja MATLAB:n yhteispelin suhteen on oivallista, että koodit ovat suoraan yhteensopivia. Myös "uudet" tietorakenteet aina erinomaista harvoja matriisien rakennetta myöten ovat mukana. Toki koko joukko erikoisalojen "toolboxeja" puuttuu OCTAVEsta, ja koodien tehokkuudessa saattaa olla merkittävää eroa.
Ohjelma lopetetaan komennolla
» quittai» exittai sulkemalla hiirellä Matlab-ikkuna.
Matlab-ikkunasto mallia 2019a 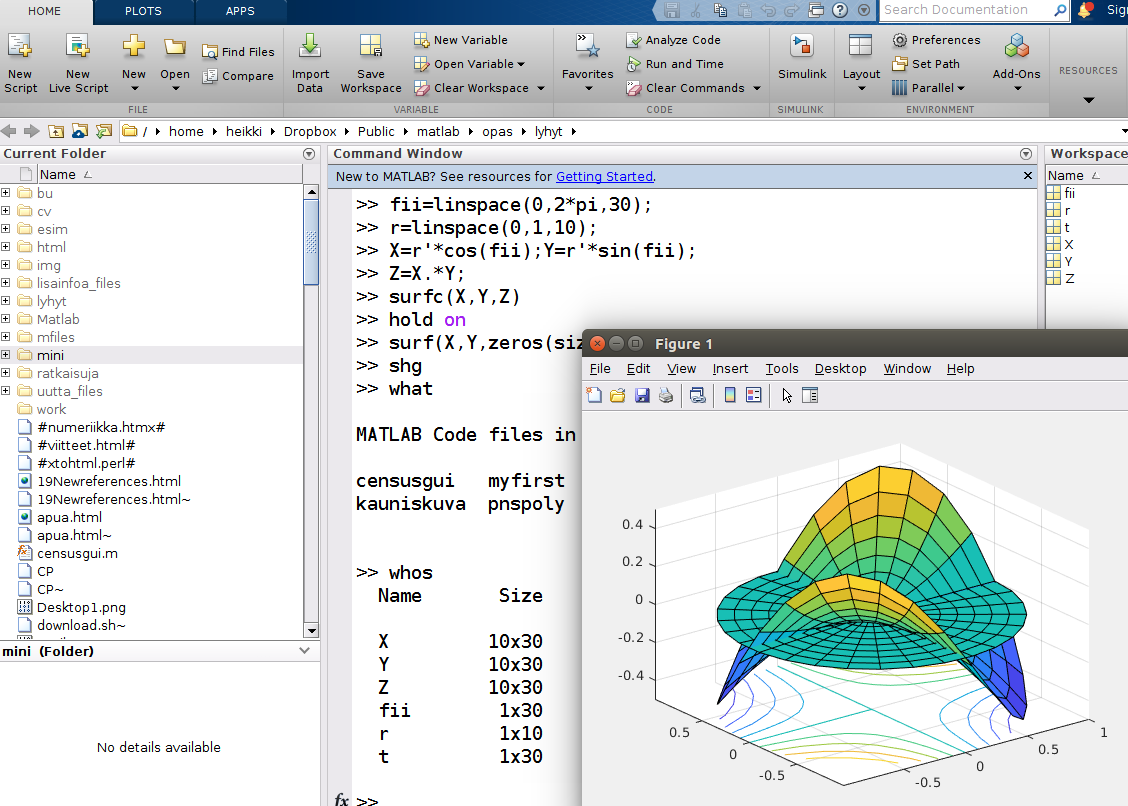
Keskellä näkyy, grafiikkaikkunan osittain peittämänä komentoikkuna, vasemmassa reunassa hakemisto- ja tiedostonäkymä, oikealla työtilan muuttujaikonit. Käyttöliittymän ulkoasua voi säädellä työkalunauhan "Layout"-ikonista.
Näkyvissä olevilla komennoilla on aikaansaatu kuvaikkunassa näkyvä grafiikka.
Viimeinen komento kokonaisuudessaan: >> surf(X,Y,zeros(size(Z)))Komentoikkunan kehotteen (>>) perään voidaan siis kirjoittaa komentoja, jotka Matlab-tulkki suorittaa. Pitemmät komentosarjat kannattaa kirjoittaa editoriin ja suorittaa sieltä, kuten kohdassa m-tiedostot, skriptit ja funktiot selitetään.
Kattava dokumentaatio käynnistyy ylänauhan (?):llä tai näppäimellä [F1] tai komentamalla >> doc (Malta odottaa hetki!)
Editori käynnistyy työkalunauhan vasemmanpuoleisilla ikoneilla, aluksi kannattanee unohtaa "Live"-tyypit, niin hienoja kuin ovatkin. Huomaa, että työkalunauha muuttuu editoritilaan. Tämän kirjoittajan mielestä kätevin tapa editorin käynnistämiseen on suoraan komentoikkunasta: >>edit omatiedosto.m
[Oppaan alkuun | "Perusteet"-sivun alkuun ]
MATLAB-työn alkuvaiheet
Edellä nähtiin joitakin esimerkkejä MATLAB-komennoista. Voit nyt ryhtyä kirjoittamaan komentoikkunaan aluksi vaikkapa ensimmäisen esimerkin mukaisesti:>> a=1 % Sijoitus muuttujaan. a = 1 % Tulos näytetään. >> b=2; % Puolipiste estää tuloksen näytön. >> c=a+b; % >> c % Muuttujan arvo saadaan kirjoittamalla sen nimi, c = 3 % kas tässä.Annettuja komentoja voi selata taaksepäin nuoli-ylös-näppäimellä, jolloin niitä voi editoida ja lähettää suoritukseen paremmalla onnella. Komennot tallentuvat "command history"-ikkunaan, josta niitä voi poimia uudelleen suorituksen, ja skriptiin eli komentotiedostoon. Yleisesti ottaen komentojen talletus on tärkeämpää kuin tulosten, koska komennot voi siistimisen ja korjailun jälkeen ajaa uudestaan. Vain lyhyehköt kokeilut kannattaa tehdä suoraan komentoikkunassa.
Suositus: Käytä aktiivisesti editoria ja hyödynnä komentojen ajamismahdollisuutta editorista käsin.Matlabin m-tiedostoja sekä työn dokumentointia (publish ja LIVE Script) käsitellään tarkemmin tässä ohjelmointia ja m-tiedostoja koskevassa osassa. kts. myös laajemman oppaan luvusta 1.3
Otetaan jo tässä kohden pikku esimerkki, joka kuvaa editorin käyttöä MATLAB-työn kehittelyssä sekä sen julkaisussa
publish-toimintoa käyttäen.Huom! Valikkotyöskentelyn sijasta voidaan editointi aloittaa suoraan komentoikkunasta kirjoittamalla: >>edit koe.m, kuten yllä jo mainittiin.
- Valitaan oma työskentelyhakemisto
- Avataan FILE-valikosta "new m-file".
- Editoidaan vaikkapa seuraavasti:
%% Matlab-dokumenttikokeilu % format compact v=1:7 % vektori [1 2 ... 7] %% Piirretään x=1:0.1:4; % vektori: alku=1, askel=0.1, loppu=4 y=sin(x); % sin:n arvot x-vektorin pisteissä. plot(x,y) %% Merkkijono >> teksti='Hello World' teksti = 'Hello World'- Talletetaan tiedostoon koe.m
Nyt voitaisiin MATLAB-komentoikkunassa kirjoittaa
koe, joka suorittaisi yllä olevat komennot.
Editorin käyttö ohjelmankehityksessä: Yllä näkyvät %%-merkit jakavat tiedoston soluihin, jotka voidaan suorittaa osina viemällä kursori solun sisään ja painamalla CTR-ENTER. Erittäin hyödyllistä. Lisäksi kaksoisprosentteja seuraavat tekstit tulevat otsikoiksi julkaisuun, joka syntyypublish-komennolla/valinnalla.
Publish-kokeilu:,
Kun haluamme hienon html-dokumentin, haemme editorin Työkalunauhasta "publish"-välilehden, jonka oikeassa reunassa näkyy "publish"-ikoni. Siitä päästään suoraan julkaisemaan tiedostommekoe.mMATLAB tekee meille kauniin html-dokumentin kuvineen kaikkineen. Doku löytyy alihakemistosta html tiedostonakoe.html. Tässä tapauksessa se näyttää tältä.
Jos halutaan panna vielä paremmaksi, voidaan työ ajaa LIVE-editorilla vieläkin tyylikkäämmäksi pdf-dokumentiksi (vuoden 2016 jälkeisissä versioissa). Palataan tähän.OCTAVEsta nämä julkaisuominaisuudet puuttuvat, paras lienee yleensä "copy/paste" soveltuvin osin esim. $\LaTeX$- tai Word-dokumenttiin. MATLAB/OCTAVE:ssa on myös vanha
diary-komento istunnon tallennukseen. Se voi olla hyödyllinen pitkissä eräajoluonteisissa töissä.Muuttujat ja sijoitus
(nimi = arvo)
- Kaikki "järkevät" merkkijonot voivat esiintyä muuttujan nimenä, numeroalkuiset eivät.
- Isot ja pienet kirjaimet erotellaan ("case sensitivity").
- Joitakin varattuja vakionimiä on, kuten
pi(siis $\pi$ ) sekäijaj, molemmat viimemainitut edustavat imaginaariyksikköä. Muita vakionimiä ovat mm. realmax, realmin, eps, Inf, NaN.
>> [i;j] % Imaginaariyksiköt sarakevektorina ans = 0 + 1.0000i 0 + 1.0000i >> realmax % Suurin liukuluku ans = 1.7977e+308 >> eps % "Kone epsilon", suhteellisen tarkkuuden raja. ans = 2.2204e-16 >> 1/0 ans = Inf % "ääretön" >> 0/0 ans = NaN % "Not a Number"Sijoitusoperaattorina on
=, siis komentox=1antaa muuttujallexarvon yksi. Puolipiste estää tulostuksen. Useampia komentoja voidaan kirjoittaa samalle riville puolipisteellä tai pilkulla erotettuna. Edellisessä tavassa siis tulostus estetään. Kokeile seuraavia:x=2;y=3; x=2,y=3Arvon voi poistaa komennolla
clear. Pelkkäclearpoistaa kaikki arvot,clear xpoistaa arvonx,
clear x ypoistaa arvotxjay, jne.
Huom:clearon esimerkki ns. systeemikomennosta, jonka syntaksi poikkeaa funktiosyntaksista, kts. alla.
Jatka kokeilua, tässä näytetään vain syötteet.x=1; y=2.2; z=-3.3; % Annetaan arvot muuttujille x,y,z x,y,z % Pyydetään Matlabia näyttämään arvot. clear x who % Mitä muuttujia on määritelty? clear y z who % Mitään ei enää näy, kun kaikki "kliirattiin". x=1,y=[1 2 3],z=[-pi i 1;1-i,5,1+i] % Luotiin skalaari x, vektori y ja (kompleksinen) matriisi z % Luvut ovat 16-numeroisia liukulukuja. % luku 1 ja 1.0 ovat identtisiä (toisin kuin vaikkapa Maplessa). A=magic(3) % Seuraavaksi lisää "systeemikomentoja": who % Lista määritellyistä muuttujista. whos % Lisäksi muuttujien koko. why % Leikitään vähän. type why % Katso koodia, voit laajentaa haluamillasi evästyksillä.Tee omia lisäkokeiluja.
Muistathan aktivoida komentojen help ja doc käytön. Edellinen on nopeampi ja suppeampi, jälkimmäinen avaa selaimen ja laajemman dokumentaation.
Esim:help clear, help who, help '='.
Viime mainittu antaa luettelon aiheesta "operators and special characters".Huom: Komentoja
clear, who, whos, helpvoidaan kutsua "systeemikomennoiksi", ne eivät noudata yleistä Matlab-funktioiden syntaksia, joka on muotoafun(arg), siis funktion argumentit ovat suluissa, mutta "systeemikomentojen" eivät. Muita systeemikomentoja ovat esim. load, save. Tässä pieni taulukko systeemikomennoista.Huomaa Google. Nopea tapa tässäkin asiassa on kysyä suoraan yleistietäjältä. Esim matlab help whos antaa neuvoja, tai vaikka Octave help load .
Vakioluonteiset muuttujasymbolit
Yllä esiteltiin matemaattisia vakioita edustavia muuttujasymboleja:pi(siis),
i, j, epsja eräitä muita. Niillä on käynnistyksen taiclear-komennon jälkeen vallitsevassa alkutilassa nimensä mukaiset arvonsa. (Kts. esimerkkiä yllä.)
Tässä taulukko joistain erikoismuuttujista
Erkoismuuttujien nimiä voidaan käyttää muihinkin tarkoituksiin. Tämä ei yleensä ole suositeltavaa. Esimerkiksi on vaikeaa löytää perustelua sinänsä luvallisille sijoituskomennoille
pi=3taiInf=-5. Sensijaanijajovat niin luontevia matriisin indeksin nimiä, että niitä ei ole tarpeen vältellä (ainakaan reaalisella matriisilla operoitaessa).Esimerkissä käytetään (seuraavasta klikattavaa) for-silmukkaa, kts. myös: >> help for tai Google: Matlab help for,
Octave help for>> format compact % Tiivistetty tulostusasu >> for i=1:3 % for-silmukkarakenne, josta ... for j=1:3 % .. lähemmin tuonnempana a(i,j)=1/(i+j-1); end end >> a a = 1.0000 0.5000 0.3333 0.5000 0.3333 0.2500 0.3333 0.2500 0.2000 >> i,j i = 3 j = 3 >> clear i j >> i,j ans = 0.0000 + 1.0000i ans = 0.0000 + 1.0000iJos suoritat samassa istunnossa kompleksilukulaskentaa, on siis muistettava "vapauttaa" muuuttujat i,j niille käyttäjän asettamista arvoista, siis clear i j , jolloin systeemin määräämät erityisarvot astuvat voimaan.Kokeile myös komentojonoa:
>> pi=3 , clear pi, pi.Muuttuja ans
Erikoisasemassa olevista muuttujannimistä eniten käytetty lienee muuttujaans, joka sisältää aina edellisen komennon tuloksen. Tarkemmin sanottuna komennon, joka ei sisällä sijoitusta johonkin nimettyyn muuttujaan. Esimerkiksi jos suoritatpi^3(siis potenssiinkorotus) ja haluat jälkeenpäin sijoittaa tuloksen johonkin muuttujaan, niin se onnistuu suorittamallax=ans. Edellistä aikaisemmin (ilman muuttujaan sijoitusta) syntyneisiin tuloksiin ei tällä tavalla voi viitata.)Laskentatarkkuus, näyttöasu, lukujen esitys, format
Matlab laskee liukuluvuilla n. 16:n (10-järjestelmän) numeron tarkkuudella.
Komennolla format voidaan vaikuttaa näyttöasuun ja vain siihen, laskentatarkkuuteen se ei vaikuta. Lukujen esityksessä käytetään desimaalipistettä, ei missään tapauksessa pilkkua . Tämä on yksi mahdollinen virhelähde aktiivisille taulukkolaskentaohjelmien käyttäjille. Matlabissa, kuten yleensäkin tieteellisen laskennan ohjelmointikielissä pilkku on varattu data-alkioiden erottimeksi. Matlabin ja Excelin väliset konversiotyökalut tekevät muunnoksen automaattisesti, käyttäjän tulee vain muistaa toimia kulloisenkin ohjelman omilla säännöillä.Tulostuksen esto, puolipiste (;)
Kyseessä on tärkeä merkki, puolipiste (;) komennon lopussa. Kannattaa siirtää selkäytimeen suosiolla, muussa tapauksessa sitten kantapään kautta. Jos kuitenkin haluat nähdä muuttujan sisällön, kirjoita vain sen nimi komentokehotteeseen. Suuren matriisin (A) tapauksessa kannattaa katsoa ensinsize(A)ja sitten vaikkapaA(1:5,1:10).** MIETI, tarvitaanko seuraavaa istuntoa ** Kommentoitiin pois, ehkä jotain lyhempää format:sta? **
Funktioita
MATLAB tuntee mm. seuraavat alkeisfunktiot:
abs,sign,sqrt,exp,log,log10,sin,cos,tan,asin,acos,atan,sinh,cosh,tanh.Täydellisen luettelon MATLAB:n tuntemista alkeisfunktioista saat komennolla
help elfun("elementary function")help specfun("special function").help elfun("elementary function"). Lisäksi on käytössä laaja joukko ns. erikoisfunktioita, kts.help specfun("special function").
Omien funktioiden määrittelyä kutsutaan ohjelmoinniksi. Tästä tarkemmin ohjelmointia ja m-tiedostoja käsittelevässä osuudessa.
"Vektori(taulukko)älykkyys": Matemaattiset funktiot (niin "elfun" kuin "specfun") ja monet muut toimivat matriiseille (ja erityisesti vektoreille) niin, että ne palauttavat argumenttimatriisin kokoisen tulosmatriisin. Siten esim.
>>y=sin(x)palauttaa x-vektorin pituisen y-vektorin, jolle $y(k)=sin(x(k)), k=1\ldots n, $ missä $n$ on $x$-vektorin pituus.
Omat funktiot kannattaa yleensä kirjoittaa "taulukkoperiaatteella".
Perusteet: Yhteenveto
- Muuttujien ja funktioiden nimissä isot ja pienet kirjaimet erotetaan ("case sensitive"), muuttujan nimi ei saa alkaa numerolla.
- Muuttujan nimen kirjoittamalla saadaan sen sisältö ruudulle.
- Puoipiste nimen perässä estää tulostuksen.
- Erikoismuuttujia:
pi,i,j,eps,Inf,NaN,...- MATLAB käyttää sulkuja:
( ), [ ], { }. "Systeemikomennot, kuten clear, load, save, format toimivat ilman sulkuja ja erotinpilkkuja.- Komento
formatvaikuttaa tulostukseen, mutta ei laskentatarkkuuteen.- Nuoli ylös ja alas selaavat komentohistoriaa. Vanhan komennon alku ja nuoli ylös täydentää komennon (jos mahdollista). Kirjoittamalla funktion nimen alun voit yrittää täydentää TAB:lla.
help aihe, doc aihea:h:b luo vektorin [a,a+h,a+2h,...,b], oletus:h=1- Tekstitiedostoon (m-tiedostoon), kuten koe.m yllä, voidaan koota komentoja, jotka suorittuvat komennolla
>> koe(myös OCTAVESSA). MATLAB:ssa tiedosto voidaan jakaa soluihin %%-merkeillä ja ajaa solu kerrallaan. Publish-valinta ajaa tiedoston html-dokumentiksi.- Matemaattiset funktiot ovat yleensä "taulukkoälykkäitä" ("array smart").
exit, quitlopettaa MATLAB:n.
[Sisällys]
Matriisin määritteleminen
Alunperin MATLABissa oli olennaisesti vain yksi tietorakenne, m×n- numeerinen matriisi, jonka alkiot ovat reaali- tai kompleksilukuja. Käsite "matriisi" sisältää erikoistapauksenaan "vektorin" ja luvun eli "skalaarin", joka ajatellaan
1 x 1-matriisiksi.
Reaalilukujen erikoistapauksena ovat kokonaisluvut ja niiden joukossa erityisesti loogiset arvot0ja1. Yleensä käyttäjän ei tarvitse huolehtia lukujen tyyppimuunnoksista, paitsi joissakin, erityisesti loogisia vektoreita ja matriiseja koskevissa tapauksissa. Lukujen lisäksi myös merkkijonoja"string"voidaan käsitellä. Versiosta 5 alkaen on käytössä myös useampiulotteiset matriisit sekä solumatriisit, joiden alkiot voivat olla itsekin (solu)matriiseja, sekä ns. struktuurit (struct). Näistä puhutaan tarkemmin tuonnempana.Varsin pitkälle pärjätään perinteisillä 2-ulotteisilla
(m x n)- matriiseilla.
Kun vektori ajatellaan matriisin erikoistapauksena, on eroteltava vaaka- eli rivivektori ((m x 1)-matriisi) ja pysty- eli sarakevektori ((1 x n)-matriisi).Matriisi voidaan määritellä usealla eri tavalla:
- Annetaan matriisin alkiot listana.
- Käytetään valmiita funktioita.
- Luodaan m-tiedostossa.
- Ladataan ulkoisesta tiedostosta.
Helpoin tapa pienimuotoisissa tehtävissä on kirjoittaa matriisin alkiot riveittäin käyttämällä hakasulkeita ja erottamalla rivit puolipisteellä, esimerkiksi
» a=[1 2 3;4 5 6;7 8 9] a = 1 2 3 4 5 6 7 8 9Suuremmissa matriiseissa voidaan syöttö katkaista usealle riville, jolloin rivinvaihto korvaa puolipisteen. (Oikeasti suurissa käytetään usein load- ja save-komentoja.)
» a=[1 2 3 4 5 6 7 8 9] a = 1 2 3 4 5 6 7 8 9Jos näytön leveys ei riitä (tai vaikka riittäisikin), voidaan riviä jatkaa kolmella pisteellä(...)tähän tapaan:>> v=[1 2 3 4 ... 5 6 7 8 9] v = 1 2 3 4 5 6 7 8 9Standardi tapa tämän nimenomaisen vektorin luomiseen olisiv=1:9, kuten kohta opimme. (Nokkelimmat oppivat sen ehkä jo tässä ja nyt.)Matriisin rivin alkiot voidaan erottaa toisistaan yhtä hyvin välilyönnillä kuin pilkulla. Voimme käyttää myös mitä tahansa MATLAB-laskutoimituksia alkioiden laskemiseksi, esimerkiksi
» x=[-1.3,4/5,4*atan(1)] x = -1.3000 0.8000 3.1416Käytössä on suuri joukko valmiita MATLAB-funktiota, jotka tuottavat matriiseja:
» b=hilb(5) b = 1.0000 0.5000 0.3333 0.2500 0.2000 0.5000 0.3333 0.2500 0.2000 0.1667 0.3333 0.2500 0.2000 0.1667 0.1429 0.2500 0.2000 0.1667 0.1429 0.1250 0.2000 0.1667 0.1429 0.1250 0.1111 » c=rand(5) c = 0.2190 0.3835 0.5297 0.4175 0.5269 0.0470 0.5194 0.6711 0.6868 0.0920 0.6789 0.8310 0.0077 0.5890 0.6539 0.6793 0.0346 0.3834 0.9304 0.4160 0.9347 0.0535 0.0668 0.8462 0.7012Tarkkaavainen lukija huomannee, että muuttujien esittelyn yhteydessä olleessa esimerkissä muodostimme itse asiassa matriisinhilb(3).
[Sisällys]
Matriisilaskentaa
Matriisilaskentaan liittyviä kertausyhteenvetoja
Lineaarialgebran kertaustiivistelmä 1, matriisit ja lineaariset yhtälösysteemit
Lineaarialgebran kertaustiivistelmä 2, ominaisarvoteoriaa
Matriisien välillä toimivat suoraan perusoperaatiot
eli yhteenlasku, vähennyslasku, kertominen, jakolaskut (vasen ja oikea), potenssiin korottaminen, sekä transpoosi. Näissä täytyy operoitavien matriisien tietenkin olla toisilleen sopivaa tyyppiä, eli yhteenlaskussa samanmuotoiset, kertolaskussa "kertomiskelpoiset" jne.
+-*/\^'» a=[1 2 3;4 5 6;7 8 0], b=a' a = 1 2 3 4 5 6 7 8 0 b = 1 4 7 2 5 8 3 6 0 » x=[-1 0 2]' x = -1 0 2 » c=a+b c = 2 6 10 6 10 14 10 14 0 » y=x-1 y = -2 -1 1 » x'*y % Vaaka kertaa pysty on vektorien sisätulo ans = 4 » x*y' % Pysty kertaa vaaka on vektorien "ulkotulo" ans = 2 1 -1 0 0 0 -4 -2 2 » 5*a-10 ans = -5 0 5 10 15 20 25 30 -10Vähennyslaskussa näkyi esimerkki ns. skalaarin laajennussäännöstä. Sovellettaessa ("pisteittäistä", kts. alla) laskutoimitusta skalaarin ja matriisin välillä, laajennetaan skalaari samankokoiseksi vakiomatriisiksi.
Yhteen- ja vähennyslasku edellyttävät samanmuotoisia matriiseja, ja ne toimivat siten, että vastinalkioille tehdään ko. operaatio.
Matriisien kertolasku toimii eri tavalla. Usein on kuitenkin tarvetta kertoa matriiseja myös vastinalkioittain. Erityisesti tämä tarve on hyvin usein vektoreilla operoinnissa. Koska kertomerkki (*) on varattu matriisikertolaskulle, täytyy "pisteittäiselle" kertolaskulle varata oma merkkinsä:Sama pätee myös mm. jakolaskuun ja potenssiinkorotukseen nähden.
Usein puhumme tässä yhteydessä taulukko-operaatioista. (Yhteen- ja vähennyslasku ovat luonnostaan "taulukko-operaatioita".)Esimerkki taulukko-operaatioista
» a=[1 2 3;4 5 6;7 8 0], b=a' a = 1 2 3 4 5 6 7 8 0 b = 1 4 7 2 5 8 3 6 0 » a.*b ans = 1 8 21 8 25 48 21 48 0 » a./b ans = 1.0000 0.5000 0.4286 2.0000 1.0000 0.7500 2.3333 1.3333 NaNYhteenveto:
Alkioittaiset, eli "pisteittäiset" laskutoimitukset (eli taulukko-operaatiot) ovat
+-.*.^./Ensin mainitut (
+,-) toimivat "luonnostaan" pisteittäin (niihin ei siten lisätä pistettä). Näiden argumenttien on oltava samankokoiset matriisit tai toisen on oltava skalaari. Tällöin puhutaan skalaarin laajennussäännöstä: skalaari osaa laajentua toisen argumentin kokoiseksi vakiomatriisiksi. Tämä mahdollistaa muotoa1+A,pi.*Bym. olevat operaatiot mielivaltaisille matriiseilleA,B.
Huomaa, ettäpi*Bjapi.*Bovat samanarvoiset, koskapion skalaari. Edellinen noudattaa matriisikertolaskun sääntöä, jossa toisena osapuolena on skalaari, ja jälkimmäisessä on kyse skalaarin laajennussäännöstä.Jakomerkit
/ja\liittyvät lineaarisen yhtälösysteemin ratkaisemiseen, ja niihin palataan myöhemmin.
Pisteittäinen jakolasku on tietysti selvä asia. Tässä on kuitenkin huomattava, että nyt ei pistettä voi jättää pois tapauksessa, jossa edellinen operandi on skalaari ja jälkimmäinen on skalaarista poikkeava matriisi.
Niinpä1/vei toimi saman periaatteen mukaan kuin yllä mainittupi*B. Tämä on johdonmukaista, sillä eihän matriisilaskennassa ole määritelty, mitä tarkoittaa skalaarin jakaminen vektorilla tai matriisilla, toisin kuin kertolaskun tilanteessa. Siten pisteittäisessä jakolaskussa on aina oltava piste paitsi jos jälkimmäinen on skalaari. Turvallisinta lienee totuttautua tällöinkin käyttämään pistettä.Huom! Pisteen poisjääminen on aloittelevan MATLAB-urheilijan tavallisimpia virheitä.
Kaikki yllä luetellut alkeisfunktiot toimivat edellisen kohdan tapaan alkioittain, joten niiden argumentti voi olla myös vektori tai matriisi. Kokeile joitakin näistä edellä määriteltyihin vektoreihin/matriiseihin.
[Sisällys]
Indeksointi ja vektorit, kaksoispiste
Yksinkertainen tapa määritellä vektori perustuu kaksoispiste-merkintään, joka on muotoa
alku:lisäys:loppuJos lisäys puuttuu, se on oletusarvoisesti 1.
>> indeksit=1:7 indeksit = 1 2 3 4 5 6 7 » 0:.1:1 ans = Columns 1 through 7 0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 Columns 8 through 11 0.7000 0.8000 0.9000 1.0000Jos halutaan n kappaletta arvoja tietylle välille, voidaan tehdä esimerkiksi näin:
» n=5; x=0:1/(n-1):1 x = 0 0.2500 0.5000 0.7500 1.0000Saman asian tekee funktio linspace.
» linspace(0,1,5) ans = 0 0.2500 0.5000 0.7500 1.0000 » x=linspace(-1,1); length(x) ans = 100Jos linspace-komennon kolmas argumentti jätetään pois, saadaan annetun välin jako 100:aan yhtä pitkään osaan. Tämä on luonteva oletusarvo 2d-grafiikassa, joka usein aloitetaan muodostamalla diskreetti x-akseli, esim:x=linspace(-pi,pi). Komennolla length voidaan katsoa vektorin pituus.
Huom: linspace-komento on yleensä syytä lopettaa puolipisteellä, jottei tarvitse katsoa (kärsien) suotta näytöllä vilisteleviä numeroita. Sama koskee tietysti kaikkia ison matriisin tuottavia komentoja.
[Sisällys]
Matriisin alkio, osamatriisi, indeksointi
Matriisin yksittäisiin alkioihin voidaan viitata antamalla suluissa alkion indeksit. Antamalla indeksin paikalla vektori voidaan valita osamatriiseja.
>> A=[1 2 3 4 5;6 7 8 9 10;11 12 13 14 15] A = 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 >> A(2,3) % Yksittäinen alkio ans = 8 >> A(:,1) % 1. sarake ans = 1 6 11 >> A(2,:) % 2. rivi ans = 6 7 8 9 10 >> A(1:2,1:4) % Osamatriisi ans = 1 2 3 4 6 7 8 9 >> A(:,[1 3 5]) % Koko sarakkeet 1,3,5 ans = 1 3 5 6 8 10 11 13 15 >> A(:,2:end) % Sarakkeet toisesta viimeiseen ans = 2 3 4 5 7 8 9 10 12 13 14 15 >> A(:,3:end) ans = 3 4 5 8 9 10 13 14 15 >> A(:,3)=[-30; 40; -500] % Muutetaan 3. sarake A = 1 2 -30 4 5 6 7 40 9 10 11 12 -500 14 15Esimerkki rivioperaatioista: Gaussin eliminaatio
Matriisin osilla operointimahdollisuus tekee monet lineaarialgebran algoritmit erityisen käteviksi. Tässä näytetään "kävelemällä" tehty alku Gaussin algoritmiin. Jatkossa sitten lisätään vauhtia ja yleispätevyyttä.>> A=vander([1:5]) % Vandermonden matriisi, argumenttivektori % ilmaisee viimeistä edellisen sarakkeen. % Huomaat, että sarakkeet ovat muotoa % (1:5)'.^j (j=0...4) A = 1 1 1 1 1 16 8 4 2 1 81 27 9 3 1 256 64 16 4 1 625 125 25 5 1 >> A=fliplr(vander([1:5])) % "flip left-right", sarakkeet lopusta alkuun. A = 1 1 1 1 1 1 2 4 8 16 1 3 9 27 81 1 4 16 64 256 1 5 25 125 625 >> Amato=A; % Kopioidaan A työmatriisiksi Amato % Estetään turha tulostus. % rivi2 <- rivi2 - rivi1 >> Amato(2,:)=Amato(2,:)-Amato(1,:) Amato = 1 1 1 1 1 0 1 3 7 15 1 3 9 27 81 1 4 16 64 256 1 5 25 125 625Tässä voitaisiin jatkaa nuolinäppäiniteraatiota editoimalla komentoriville 2:n paikalle 3,4,5. Siirrytään kuitenkin kevyeen hölkkään:>> for i=3:5 Amato(i,:)=Amato(i,:)-Amato(1,:); % Jos haluat nähdä välivaiheet, end % poista puolipiste. >> Amato Amato = 1 1 1 1 1 0 1 3 7 15 0 2 8 26 80 0 3 15 63 255 0 4 24 124 624Ensimmäisen sarakkeen tukialkion alapuolinen osa on nollattu ja siirrytään toiseen sarakkeeseen, tukialkiona edelleen mukavasti1. Mutta eipä jatketa tällä kertaa pidemmälle.
Tässä käytettiin muuttujaaiindeksinä, kuten luontevaa on.>> i i = 5 >> clear i >> i ans = 0 + 1.0000i % Tästä ilmiöstähän puhuttiin edellä.Tietoaineksen poimiminen loogisten ehtojen avulla
Loogisten operaattoreiden avulla voidaan myös kätevästi valita tietyt ehdot toteuttava osa vektorista tai matriisista.
Vektorin tapauksessa indeksointi suoritetaan loogisella vektorilla, joka koostuu nollista ja ykkösistä. Syntaksi on sama kuin vektorin indeksoinnissa kokonaislukuvektorilla yllä. Looginen (0-1-) indeksivektori valitsee ne (ja vain ne) alkiot, joita vastaa indeksivektorin 1 (=true).Periaate yksinkertaisimmillaan valaistukoon tällä esimerkillä:
>> v=-3:3 v = -3 -2 -1 0 1 2 3 >> v>0 % v:n jokaiselle alkiolle tehdään vertailu 0:aan. ans = 1×7 logical array 0 0 0 0 1 1 1 % 1 niille, joille ehto toteutuu. >> v(v>0) % Valitaan ne. ans = 1 2 3 % Helppoa, mahtavaa!HUOM! Numeerinen (0-1)-vektori ei kelpaa indeksivektoriksi. Mutta, mikä hauskaa, loogisella vektorilla voi laskea, mitä voidaan hyödyntää usein tehokkaasti. Jatketaan edellistä:>> bv=[0 0 0 1 1 1 1 ] 0 0 0 1 1 1 1 >> lv=logical(bv) lv = 1×7 logical array 0 0 0 1 1 1 1 >> v(bv) Subscript indices must either be real positive integers or logicals. >> v(lv) ans = 0 1 2 3 >> lv+lv ans = 0 0 0 2 2 2 2 >> true ans = logical 1 >> true+true ans = 2 % HAH! >> sum(lv) % Kuinka moni v:n alkio >=0 (ei-negat). ans = % Laskettiin siis (loogisten) ykkösten (ja nollienkin) summa. 4Esim. ns. "elävästä elämästä"
Olkoon annettu vektori, jonka alkiot ilmaisevat isojen hallirakennusten kriittisten palkkien varmuuskertoimia. Muutamien hallisortumien jälkeen on tullut voimaan määräys, että varmuuskertoimien on oltava vähintään 3. Tehtävänä on valita vektorista kelvolliset varmuuskertoimet.>> vk=[1 3 4 2 5 6 2 1 6 7 4 5 3 2 1 2 3] % Muodostetaan % varmuuskertoimien vektori. vk = Columns 1 through 13 1 3 4 2 5 6 2 1 6 7 4 5 3 Columns 14 through 17 2 1 2 3 >> vk >= 3 % Mitkä ovat vähintään 3 ? ans = Columns 1 through 13 0 1 1 0 1 1 0 0 1 1 1 1 1 Columns 14 through 17 0 0 0 1 >> % Tuloksena looginen vektori, jossa 1 vastaa ehdon toteutumista. >> vk(vk>=3) % Indeksoidaan loogisella vektorilla. ans = 3 4 5 6 6 7 4 5 3 3Jatkokäsittelyn kannalta on usein hyödyllistä poimia ehdon toteuttavan osavektorin indeksit. No sehän käy näin:>> N=length(vk); >> indeksit=(1:N) indeksit = Columns 1 through 12 1 2 3 4 5 6 7 8 9 10 11 12 Columns 13 through 17 13 14 15 16 17 >> varmuusindeksit=indeksit(vk>=3) varmuusindeksit = 2 3 5 6 9 10 11 12 13 17Huomaa, että Matlab-tulkki ei hyväksy lauseketta(1:N)(vk>=3), joka käyttäjän mielestä tuntuisi ihan oikealta. (Joitakin muita vastaavia rajoituksia esiintyy, "kukaan ei ole täydellinen".)
Yllä olevat varmuusindeksit saataisiin vieläkin vaivattomammin find-komennolla.>> find(vk>=3) ans = 2 3 5 6 9 10 11 12 13 17Jatketaan loogisen indeksoinnin parissa:Periaate: Komento
>> vk >= 3vertaa vektorinvkjokaista alkiota oikeaan puoleen (3) ja palauttaavk:n pituisen loogisen vektorin, jossa on 1 niillä kohdilla, joilla ehto toteutuu ja 0 muuten.
Kun vektoria (tässävk) indeksoidaan samanpituisella loogisella vektorilla, poimitaan ykkösiä vastaavat alkiot ja vain ne.
Kannattaa myös huomata, että tässä yhteydessä komento find on hyödyllinen ja tekee jotkin asiat vieläkin helpommiksi, kuten juuri nähtiin.
Suurilla datoilla kannattaa tehokkuussyistyä yleensä suosia loogista indeksointia, se on tehokkaampi kuin find:n käyttö.Aihetta käsitellään enemmän näillä kohdin laajemmassa oppaassamme. (Siellä saattaa olla "vanhanaikainen", tehokkuutta huomioonottamaton suositus.)
Toinen, vähän suurempi esimerkki: Muodostetaan yksikkövälillä (0,1) tasaisesti jakautuneista satunnaismuuttujista koostuva 100:n alkion pituinen vektori. Voidaan kysyä vaikka seuraavia:
- Kuinka moni on vähintään 0.2 ?
- Mikä on kaikkien näiden summa?
- Kuinka moni on välillä (0.4,0.6) ?
- Poimi kaikki viimeksi mainitulla välillä olevat!
v=rand(1,100); >> sum(v>0.2) % Lasketaan yhteen kaikki ykköset. ans = 82 >> length(v(v >= 0.2)) % Sama myös näin (vrt. edellä). ans = 82 >> sum(v(v >= 0.2)) ans = 50.9311Jätämme loput harjoitustehtäväksi. Huomaa, että looginen operaattori "and" on MATLAB:ssa&Jos tietoaines on vaikkapa matriisissa
A, on useissa tapauksissa kätevintä jonouttaa matriisi ensin pitkäksi vektoriksi näin:Takaisin alkuperäiseen muotoon palataan tarvittaessa kätevästi komennolla reshape .
>> v=A(:);ESIMERKKI
» x=fix(rand(100,1)*100); % Generoidaan satunnaisvektori » length(x(x>90)) % Kuinka monta alkiota > 90 ans = 9 » ind=find(x>90); % Etsitään näiden indeksit » ind(1) % Ensimmäinen niistä ans = 17 » x(17) ans = 98Looginen indeksointi, esimerkkejä, viitteitä, tehtäviä
[Sisällys]
Matriisifunktioita
Käytettävissä on runsas valikoima valmiita matriisifunktioita.
"Matriisijakolasku" ja eräitä muita matriisifunktioita
Matriisilaskennassa ei puhuta yleensä jakolaskusta, mutta mikään ei estä ottamasta käyttöön luvuilla laskemisen analogiaa: Jakolaskub/atarkoittaa yhtälöna*x = bratkaisua, mikäli sellainen on olemassa, ts. mikälia~=0(Matlab-notaatiolla).
Matriisilaskennassa kerto- ja jakolaskujen järjestykseen pitää kiinnittää huomiota. Siksi vastaava lasku matriiseille kirjoitetaan tavanomaisessa tapauksessa:x=A\bMuistisääntö: Vektori (tai matriisi)bjaetaan matriisillaA, jotenAon jakoviivan alapuolella.
(Hiukan "oudomman näköisen" yhtälönx*A = bratkaisulle on varattu "etukenoviiva":x=b/A. Huomaa, että matriisiAon jälleen jakoviivan alapuolella.)Esimerkki:
» format compact % Tiivis tulostus » A=[1 -1 0;2 0 3;-5 4 1] A = 1 -1 0 2 0 3 -5 4 1 » det(A) % Determinantti ... ans = % on nollasta poikkeava, joten A on ei-sigulaarinen. 5 » b=[1;1;1] b = 1 1 1 » x=A\b % Ratkaistaan systeemi A*x=b x = -2.8000 -3.8000 2.2000 » inv(A) % Käänteismatriisi ans = -2.4000 0.2000 -0.6000 -3.4000 0.2000 -0.6000 1.6000 0.2000 0.4000 » ans*b % Sama tulos, edellinen tapa on suositeltavampi ans = -2.8000 -3.8000 2.2000Matriisin jakolaskut voidaan ilmaista käänteismatriisin avulla näin: Oikealta jako
A/Btarkoittaa matriisia AB-1 ja vasemmalta jakoA\Bmatriisia A-1B. Vasemmalta jako\laajenee myös tapauksiin, jolloin käänteismatriisia A-1 ei ole olemassa. TällöinA\bon lineaarisen yhtälöryhmän Ax=b pienimmän neliösumman ratkaisu. Tähän palataan esimerkein myöhemmin. Katso myöshelp \.Alkuvaiheessa riittänee hyvin keskittyä takakenoviivalla operointiin eli vasemmalta jakoon. (Tavallista jakoviivaa on luonnollista käyttää, kun toinen operandi on skalaari, tällöin on aina syytä laittaa piste mukaan, kuten edellä tähdennettiin.)
Muistisääntö: Kummassakin jakolaskussa jakaja on jakoviivan alapuolella.
Numeeriseen algoritmiin liittyvä huomio: Yhtälöryhmän ratkaisua varten ei lasketa käänteismatriisia.Ominaisarvot ja -vektorit
Kätevä ja tehokas työväline on ominaisarvoja ja -vektoreita numeerisesti laskeva eig-funktio. Samalla nähdään esimerkki funktiosta, joka palauttaa useamman kuin yhden tuloksen.>> eig(A) % Kutsuttaessa ilman muuttujaa tai yhdellä muuttujan... ans = % nimellä, saadaan pelkät ominaisarvot. -1.6346 -0.7049 4.3395 » [V,D]=eig(A) % Normeeratut ominaisvektorit V:n sarakkeina. V = -0.2844 -0.4452 -0.1536 -0.7494 -0.7590 0.5130 0.5979 0.4751 0.8445 D = % Ominaisarvot D:n lävistäjällä. -1.6346 0 0 0 -0.7049 0 0 0 4.3395
[Edellinen] [Seuraava] [Sisällys]