MATLAB-opas, grafiikkaa

Päivitys: 20.8.2019

Oppaan etusivu

Grafiikkasivun sisällys

plot | subplot | Kompleksipiirto plot:lla | fplot | parametrimuotoinen piirto plot:lla
plot3: avaruuskäyrät | mesh,surf,contour:pinnat ja korkeuskäyrät

MATLAB sisältää monipuoliset piirtokomennot datan 2- ja 3-ulotteiseen visualisoimiseen.

Komennon plot perusmuoto

Tässä on Mathworks'n ohjeet: >>doc plot ja >>doc plot3 Funktio plot toimii periaatteella:"Yhdistä xy-datapisteet niiden kautta kulkevalla murtoviivalla" !
Esimerkiksi: 
    >> x=[1.5 2.2 3.1 4.6 5.7 6.3 9.4];
    >> y=[2.3 3.9 4.3 7.2 4.5 6.1 1.1];
    >> plot(x,y);grid on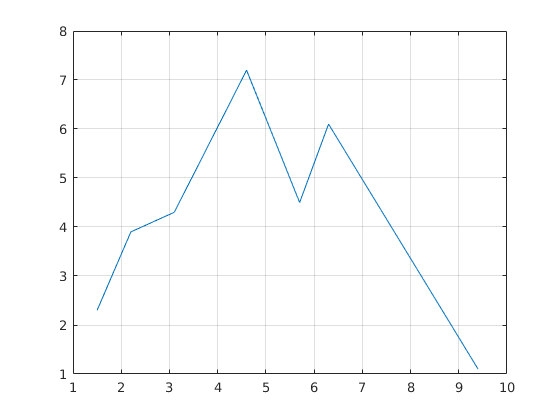
basicplot1

Käyrien piirtäminen

Käyrät piirrretään diskretoimalla riittävän tiheästi plot-komennolle annettava data.

Ajatellaan, että haluamme piirtää käyrän \(y=x^3-2x+1\) välillä [-2,2].

Muuttujaksi x otetaan sataan osaan diskretoitu x-akselin väli. 
» x=linspace(-2,2,100);
Luvun 100 voi jättää pois, sillä 100 on oletusarvo. Lasketaan y-vektoriin vastaavat funktion arvot. Huomaa (.^) 
» y=x.^3-2*x+1;
Komento 
 » plot(x,y)
piirtää siis x-vektorin ja y-vektorin vastinkomponenttien ilmaisemien koordinaattipisteiden (x(i),y(i)), määräämän murtoviivan. Kun pisteitä on tarpeeksi (usein 100 riittää), saadaan sileä käyrä kuvaksi.

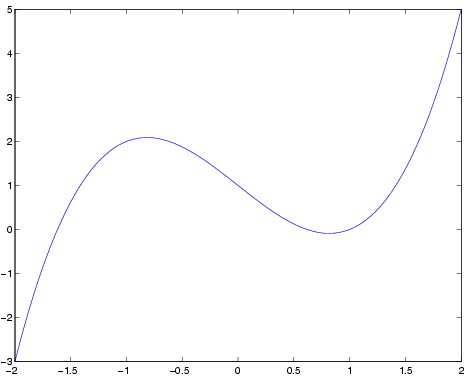
plot1

Kokeile minkälaisen käyrän saat jos 100:n sijasta käytät arvoa 10.

Koordinaatisto muodostuu automaattisesti niin, että kaikki piirtodata juuri mahtuun kuvaan.

Kuvan skaalausta voi muuttaa komennolla axis([xmin xmax ymin ymax]) , kts: axis.

axis-komennon argumenttina voi olla myös erinäisiä merkkijonoja, joista useimmin tarvittavia lienevät axis('equal'), axis('square'). Alkutilaan päästään komennolla axis('normal').

axis('equal') ja axis('square'), jotka muuten voi antaa myös tyyliin axis equal, ovat erityisen tarpeellisia silloin, kun halutaan esim. ympyrän näyttävän ympyrältä.

xlim, ylim -komenoilla muutetaan vain x- tai y-akselin rajoja.

Kokeile miten äsken saamasi kuva muuttuu kun käytät yllä mainittuja axis-komennon eri muotoja. Kuvaa voi käsitellä kuvaikkunan työkalunauhan valikosta näkyvillä tavoilla.
Sitä voi "zoomata" (suurennuslasi), kuvaan voi lisätä tekstejä (insert-valikosta "text") jne. Samoja asioita voi hoitaa myös komennoilla, kuten zoom on.

Jos haluat piirtää toisen käyrän jo olemassaolevaan kuvaan, niin anna komento hold on. Tämän jälkeen kaikki seuraavat käyrät tulevat edellisten 'päälle', kunnes annetaan komento hold off.
Piirrä yllä saadun käyrän kanssa samaan kuvaan $$y=2\cos(x^2-5x+17).$$

Toinen tapa usean käyrän piirtämiseksi samaan kuvaan on plot-komennon muoto plot(x1,y1,x2,y2,x3,y3,...). plot-komennossa voi lisätä viivatyyppimääreen kullekin haluamalleen käyrälle.
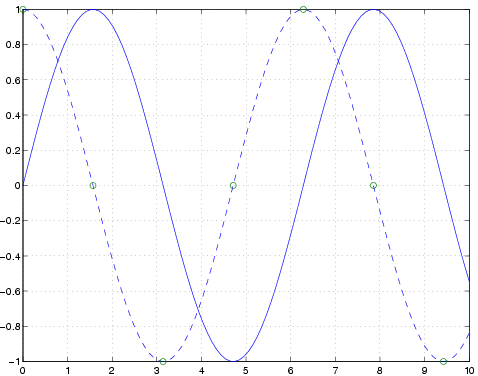
Jos haluttaisiin vaikkapa piirtää sinikäyrä sinisellä, kosinikäyrä katkoviivalla ja lisäksi merkitä jälkimmäiselle rinkuloilla kaikki pi/2:n monikerrat välillä [0,10], olisi sopivaa tehdä näin: 

» x=linspace(0,10);
» x1=0:pi/2:10;
» plot(x,sin(x),'b',x,cos(x),'--',x1,cos(x1),'o')
» grid
plot

Huom 1: plot(x1,cos(x1),'o') ('o' :n sijalla käy esim. 'x' tai '.') piirtää vain ao. pisteet, mutta jättää yhdistysjanat piirtämättä.

+++** Taulukko kaikista markkerityypeistä **+++

Huom 2: Yleinen muoto on plot(x1,y1,'mjono1',x2,y2,'mjono2',x3,y3,...), missä 'mjono1', 'mjono2',... ovat yllä esiintyvän tyylisiä merkkijonoja, joilla ilmaistaan väri tai viivatyyppi.
Argumentit voidaan mieltää kolmikoiksi, yksi kolmikko kutakin piirrettävää käyrää kohti. Mistä tahansa kolmikosta voidaan jättää merkkijono-osa pois, jolloin ko. käyrä piirretään oletusvärillä ja -tyypillä.

Komennolla grid- voidaan kuvaan lisätä koordinaatti- (hila-) viivat, mikä on usein hyödyllistä. Kokeile joitakin yllä esitetyn kaltaisia yhdistelmiä.

Uuden piirtoikkunan saa avatuksi komennolla figure. Piirtoikkunoilla on numero, jonka avulla useista ikkunoista voidaan valita se, johon halutaan piirtää: komento figure(n), missä n on ikkunan numero, figure(2) ohjaa seuraavat piirrokset ikkunaan n.

Yllä mainitussa YAGTOM-oppaassa kohdassa "Plotting curves" on tyylinäyte yksinkertaisen peruspiirroksen metamorfoosista lisävalitsimien avulla tyylikkääksi graafiseksi esitykseksi.

Grafiikkaruudun jakaminen osiin, subplot

Komento subplot(m,n,p) jakaa kuvaikkunan mxn-"kuvamatriisiksi", jossa seuraava piirtokomento kohdistuu p:nteen pikkuruutuun, kun edetään riveittäin.
ESIM: 
subplot(2,1,1);  % 2x1-"matriisin" ruutu 1.
x = linspace(0,10);
y1 = sin(x);
plot(x,y1)

subplot(2,1,2);  % 2x1-"matriisin" ruutu 2.
y2 = sin(5*x);
plot(x,y2)
subplot1
Tehtävä: Piirrä osaruudut viererekkäin!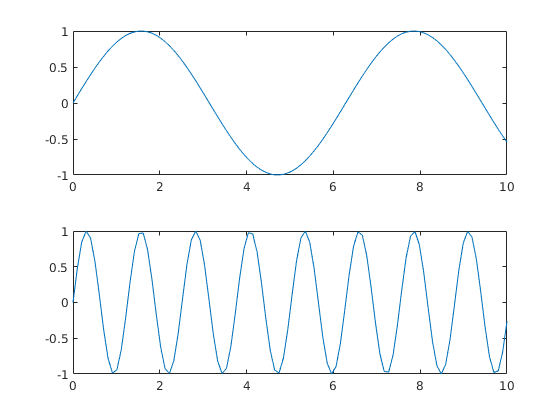

Piirtämishuomioita

Funktiossa linspace on oletusarvona jako sataan osaan, mikä on usein sopiva 2D-piirroksiin. Tavallisimmin piirto tehdään siten tähän tapaan: 

» x=linspace(a,b); % a:lla ja b:llä oltava numeeriset arvot.
» y=lauseke; %  Esim y=exp(sin(x))+x.^3;
» plot(x,y)

Toinen tapa x-diskretointiin on antaa jakovälien lukumäärän sijasta jakovälin pituus h, jolloin kirjoitettaisiin >> x=a:h:b;

Yllä kannattaa panna merkille puolipisteen käyttö, joka säästää tarpeettomalta pitkän vektorin tulostukselta.

Yhteenveto käyrän ja (x,y)-taulukon piirtämisestä
  • Muodostetaan vektorit x ja y. Ne voivat olla annettua dataa tai y-arvot ovat tarkasteltavan funktion arvoja x-pisteissä.
  • plot(x,y) piirtää tasoon (xi,yi)-pisteet yhdistävän murtoviivan.
  • plot(x,y,'o') piirtää pelkät pisteet ilman yhdistysjanoja käyttäen 'o'-merkkejä.
  • plot(x,y,x,y,'o') piirtää murtoviivan ja pisteet 'o'-merkillä.
  • grid on : Koordinaattiviivat (suosittelen yleensä).

Yhteenveto grafiikkaikkunoiden hallinnasta
  • hold on aiheuttaa edellä piirretyn kuvan jäädyttämisen, jolloin seuraavat piirtokomennot piirtävät edellisen kuvan päälle.
    Takaisin "pyyhkimistilaan": hold off
  • figure avaa uuden kuvaikkunan. Jos halutaan jatkaa piirtämistä aiemmassa tai uudessa ikkunassa, voidaan komentaa esim. figure(2)
  • shg "show graphics" tuo viimeisen grafiikkaikkunan esiin.
  • clf "clear figure" tyhjentää grafiikkaikkunan "vanhasta roskasta".
  • close all hävittää kaikki grafiikkaikkunat. Usein hyödyllinen skriptitiedoston alussa.
  • subplot(m,n,p) ruudun jako (m,n)- "kuvamatriisiksi", seuraava piirtokomento kohdistuu rutuun no. p.

Kompleksilukujen piirto

Piirtofunktion plot argumentiksi voidaan antaa myös kompleksiluku(vektori) z=[z1,z2, ...,zn] . Tällöin ohjelma piirtää näiden tason pisteiden määräämän murtoviivan tasoon, ts. plot(z) toimii samoin kuin plot(real(z),imag(z))

Esim

Piirrä kompleksitasoon pisteet 0,1,1+i,i. 

  >> plot([0,1,1+i,i,0])
  >> axis([-.2 1.2 -.2 1.2]) % Väljennetään akseleita
  >> hold on                 % Pidetään edellinen
  >> plot([0,1,1+i,i,0],'x') % Nurkkapisteet x:llä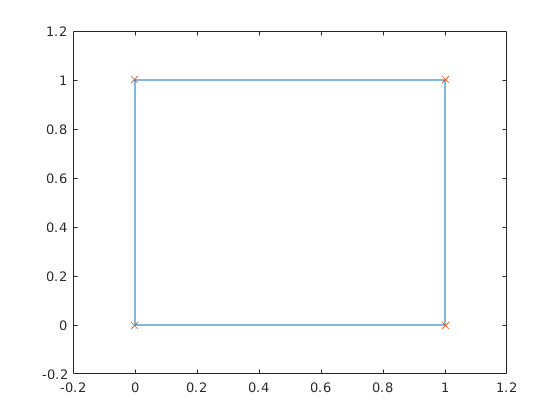
complplot1

Tehtävä: Muistele De Moivre'n kaavaa: \[e^{i\phi} = \cos(\phi) + i\, \sin(\phi). \] Piirrä tätä hyväksi käyttäen yksikköympyrä kompleksitasoon.
Vihje: Muodosta vektori phi=linspace(0,2*pi); ja sitten vain z-vektori.

Matlab-funktion piirto, fplot

fplot on vaihtoehtoinen tapa funktion piirtämiseen. Tällöin funktion on oltava joko MATLAB-funktio (kuten sin, cos, exp, ...) tai itse määritelty funktio (joko m-tiedosto tai ns. funktiokahva tai vanhanaikainen "inline"-määrittely).

Esim: fplot(@sin,[0,2*pi]) tekee saman kuin x=linspace(0,2*pi);plot(x,sin(x)). Erona on se, että fplot suorittaa ns. adaptiivisen diskretoinnin, joka mahdollistaa tarkan kuvan vähemmällä laskentatyöllä. (Toki adaptiivisyydelläkin on "hintansa", koska se haittaa "vektorointia".) 

>> f=@(x) x.^2   % Lue: f="at(x), x toiseen", vrt: f=x->x^2 (Maple)
>> fplot(f,[0,1])
Tai voitaisiin käyttää "nimetöntä funktiotyyliä": 
>> fplot(@(x) x.^2,[0 1])

Parametrimuotoiset käyrät tasossa

Funktio plot soveltuu sellaisenaan parametrimuotoiseen piirtoon. Ajatellaanpa yksinkertaisimpana esimerkkinä ympyrää, jonka luonnollinen parametriesitys on \(x=cos(t), y=sin(t), t \in \left[0,2\pi\right]\) 
>> t=linspace(0,2*pi);
>> x=cos(t); y=sin(t);
>> plot(x,y)
>> axis equal; axis square;
Tätä sopii verrata yllä olevaan kompleksipiirtoon. Esimerkkejä +++**LISÄÄ **+++

3D-grafiikka

Avaruuskäyrät

Parametrimuodossa annettuja avaruuskäyriä voidaan piirtää funktiolla plot3 lisäämällä z-koordinaatti mukaan. Esimerkki selvittäköön asian. Jatketaan parametripiirtoesimerkkiä ottamalla mukaan z-koordinaatti, joka nousee lineaarisesti kulman t funktiona. Toisin sanoen piirrämme ruuviviivan: $$x=cos(t), y=sin(t), z=t, t \in \left[0,6\pi\right]$$ 
>> t=linspace(0,6*pi);
>> x=cos(t); y=sin(t); z=t;
>> plot3(x,y,z)
>> axis equal; axis square;
>> grid
Tämä on periaatteessa sama esimerkki kuin funktion plot3 avustussivulla. Kuvakin näkyy siellä (tosin hiukan eri parametrein).

Pintapiirrokset ja korkeuskäyrät

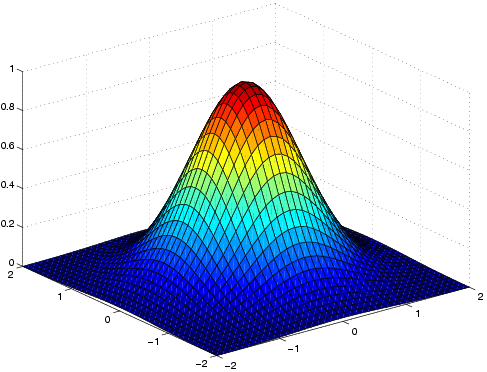
Kts. myös: Various views of meshgrid

Olkoon piirrettävänä funktion f(x,y)=e-x2-y2 määrittelemä pinta(pala) xy-tason neliön [-2,2] x [-2,2] alueella. Ajatus on, että jaetaan alue koordinaattiviivoilla suorakulmiohilaksi ja lasketaan kussakin hilapisteessä (xi, yj) funktion arvo zi,j=f(xi, yj). Näin saadaan korkeusmatriisi Z=(zi,j). Ajatellaan, että asetetaan kuhunkin hilapisteeseen (xi, yj) sauva, jonka (merkillä varustettu) pituus on zi,j. Näin syntyneen "sauvametsän" päällee asetetaan lepäämään "pintamatto".

Sama korkeusmatriisi soveltuu niin pinta- (surf), korkeuskäyrä- (contour) kuin yhdistelmäkuviin (surfc). 

» x=-2:.1:2; y=x;       % x-ja y-akselin diskretoinnit tässä samoja.
» [X,Y]=meshgrid(x,y);  % X ja Y määräävät xy-alueen hilapisteistön.
» size(X), size(Y)
ans =
    41    41
ans =
    41    41

» Z=exp(-X.^2-Y.^2);   % Korkeusmatriisin arvot hilapisteissä. 
                       % Huomaa "pisteittäiset" laskutoimitukset.
» surf(x,y,Z)             % surf-funktio "asettaa maton
                          % sauvametsän päälle".
>> contour(x,y,Z)      % Korkeuskäyräpiirros
>> ezcontour('exp(-x^2 - y^2)',[-2 2 -2 2])  % "easycontour", ei tarvita 
>>                                % meshgridiä eikä "vektorointipisteitä".
surf1
Demonstroidaan view-komentoa: 
» for j=1:5;view(-20+10*j,20*j),pause,end;
Kuvan pyörittäminen käy vuorovaikutteisemmin kuvaikkunan työkalunauhan oikeanpuolimmaisesta painikkeesta.

meshgrid

Kts. myös: Various views of meshgrid

Kyseessä on monikäyttöinen ja tehokas (ja välttämätön) komento erityisesti pinta-ja korkeuskäyräpiirroksissa. Kuten todettu, funktion f(x,y) pintaa ym. varten tarvittava data koostuu matriisista Z=(zij), missä zij = f(xi, yj), kun pisteet xi ja yj muodostavat x-alueen (vast. y-alueen) diskretoinnin.
&matlab;:ssa voitaisiin toimia näin: 

>> x=linspace(a,b,m); y=linspace(c,d,n);
>> Z=zeros(m,n);
>> for i=1:m
     for j=1:n
       Z(i,j)=f(x(i),y(j));
     end
   end
Sitten vaan: >> surf(x,y,Z') . (Miksi pitää transponoida, no mesh-, surf- ym. komennoissa ajatellaan koordinaatistoa eikä matriisin indeksejä.)

Tällainen kävisi ajan oloon hermoille (eikö vaan?). (Sekä tehotonta että vaivalloista.) Pelastuksen tarjoaa meshgrid.

Kokeillaan: 

>> x=0:3
x =
     0     1     2     3
>> y=-(0:2)
y =
     0    -1    -2
>> [X,Y]=meshgrid(x,y)
X =
     0     1     2     3
     0     1     2     3
     0     1     2     3
Y =
     0     0     0     0
    -1    -1    -1    -1
    -2    -2    -2    -2
Matriisit X ja Y ovat samankokoiset.
  • X koostuu x-riveistä allekkain. Niitä on n kpl., n = y:n pituus.
  • Y koostuu y-sarakkeista vierekkäin, niitä on m kpl., m = x:n pituus
Kun f on vektoroidusti määritelty funktio ("array smart"), niin Z=f(X,Y) on matriisi, jolle todellakin Zij = f(xi, yj).
Kun komennot mesh, surf, contour kirjoitetaan muodossa mesh(x,y,Z), ..., &matlab; antaa myös oikean koordinaatiston. Jos annetaan pelkkä matriisi Z, piirto tapahtuu matriisin Z indeksejä käyttäen aivan samoin kuin 2d plot-funktion tapauksessa.
Hilapisteet voi piirtää näppärästi: 
>> plot(X(:),Y(:),'o')
>> axis([-0.1 3.1 -2.1 .1])
Tee ja tee (selväksi). Hilaruudukon taas näin: 
>> plot(X,Y)
>> hold on
>> plot(X',Y')
(Aikamoista &matlab;-iloittelua!)

Pinta ympyräalueen päällä

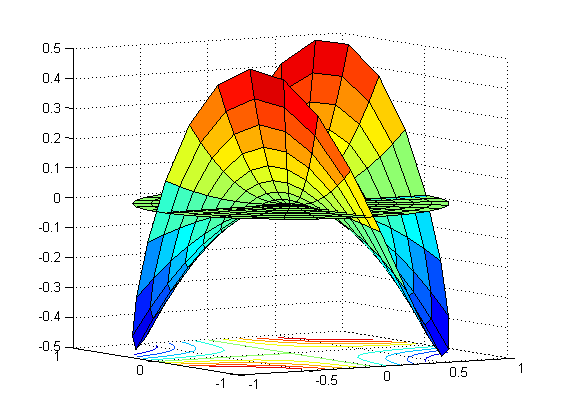
Edellä oleva pintapiirto tuntuu olevan kovasti suorakulmioalueeseen rajoittuvaa. Mutta &matlab; on moneen taipuva työkalu. Mietitäänpä ympyräaluetta. Miten voitaisiin käyttää napakoordinaattimuunnosta hyödyksi. No kokeillaan funktiota f(x,y) = x y yksikkökiekon päällä. 
>> t=linspace(0,2*pi,30);
>> r=linspace(0,1,10);
>> X=r'*cos(t);Y=r'*sin(t);  % Ulkotulot
>> Z=X.*Y;
>> surf(X,Y,Z)
>> surfc(X,Y,Z)
>> hold on
>> surf(X,Y,zeros(size(Z)))
surfnapa
EI HUONO!

Ruuviviiva lieriön pinnalla

Tässä on Nancy K. Stanton'n (Stanford University) materiaalista poimittu esimerkki: 
Tiedosto helix.m:


%% Helix on a cylinder

%%
% Here is a way to plot a helix on a cylinder.  
% It will use a parametric description of the cylinder.  The cylinder is a 
% right circular cylinder of radius 1 centered on the z-axis.  It is the
% set of all points of the form
%%
%
$$(\cos(U),\sin(U),V),\qquad 0 \le U \le 2\pi,\quad \mbox{--}\infty < V < \infty. $$ 
% 
% I'll limit the graph to 
%%
%
$$ 0 \le V \le 6\pi.$$ 
%
% I begin by making a 50x50 mesh of the points [U,V] I'll use in the graph.

u=linspace(0,2*pi,50); v=linspace(0,6*pi,50);
[U,V]=meshgrid(u,v);

%%
% To be able to get a thick curve for the helix, I use the *plot3*
% command. I plot the helix as a very thick curve and use the command 
% *surf* to plot the cylinder.   
% The command *colormap white* prevents shading of the cylinder. 

t=linspace(0,6*pi,300);
plot3(cos(t),sin(t),t,'LineWidth',3), hold on
title('Helix on a cylinder')
surf(cos(U),sin(U),V), colormap white, hold off
Jos lataat tämän m-tiedoston itsellesi (vaikka copy/paste) ja avaat sen Matlabin editorissa ja painat "Publish"-välilehteä, ja suoritat "publish", saat tällaisen tällaisen html-dokumentin.

Tässä on toinen esimerkki ympyräalueelle taipuvasta pintapiirroksesta yhdistettynä 3d-käyrän piirtoon plot3-funktiolla. Lisäksi nähdään malli m-tiedoston rakenteesta, jolla publish-työkalu tekee hienon dokumentin aina matemaattisia $\LaTeX$-kaavoja myöten. (Vielä hienomman saat avaamalla m-tiedoston "LIVE scriptinä" ja tulostamalla ajon pdf-tiedostoksi.)



m-tiedostoista ja niiden kirjoittamisesta Publish-työkalulle sopivaan muotoon puhutaan seuraavassa kohdassa. Tämä toimikoon hyvänä pohjana.

[Edellinen] [Seuraava] [Alkusivu]