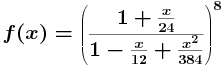Matlab-tehtäviä 2

Lausekkeita, grafiikkaa ...

• C. Van Loan-kirjan m-tiedostot

Vektoreita, matriiseja,lausekkeita, 2d-grafiikkaa

1.

Tee Matlabilla vektorit, jossa on alkiot:

1. 2, 4, 6, 8, ..., 20
2. 10, 8, 6, 4, 2, 0, -2, -4, ..., -10
3. 1, 1/2, 1/3, 1/4, 1/5, ..., 1/10
4. 0, 1/2, 2/3, 3/4, 4/5, ..., 9/10

Voit komentaa: format rational .

2.

Vektorien ja matriisien normit. Näitä tarvitaan mm. lineaarisen yhtälösysteemin häiriöalttiuden mittareina.

1. Kirjoita (nautiskellen) Matlab-lauseke, jolla lasket matriisin A ns. ykkösnormin. Se saadaan matriisin alkioiden itseisarvojen muodostaman matriisin sarakesummien maksimina. Vastaavasti ääretön-normi saadaan rivisummien avulla. No Kirjoita ja testaa vaikka satunnaislukumatriiseilla ja vertaa valmiin norm-funktion antamiin.
   Huom! uusissa Matlab-versioissa summaukseen voidaan liittää indeksisuunta, vanhemmissa edetään aina sarakkeita pitkin, jolloin rivisuunta on tehtävä transponoimalla. (Tämä uudistus oli välttämätön, kun useampiulotteiset taulukot tulivat mukaan.)
2. Neliömatriisin A "häiriöalttius", "condition number" on cond(A)= || A || || A-1|| , missä || A || on jokin matriisinormi. Tutki Vandermonden matriisien häiriöalttiutta tyyliin:

   n=2;
   x=-n:n;
   V=vander(x), VI=inv(V)
   cond1=norm(V,1)*norm(VI,1)
   

   Kasvata (varovasti) n:ää ja aja uudestaan. Mitä havaitset.
   Jos haluat, voit rakentaa pienen for-silmukan tähän tapaan:

   N=5;
   for n=1:N
          x=-n:n;
          V=vander(x); VI=inv(V);
          size(V)
          cond1=norm(V,1)*norm(VI,1);
   end;
   

   Huomaat, että format long on tarpeen.

   Matlab:ssa on funktioita: cond, condest, rcond häiriöluvun estimointiin. (Määritelmän mukaan laskeminen on suurilla matriiseilla raskasta.)
   Nyrkkisääntö: Lineaarisen yhtälöäsysteemin A x = b ratkaisussa on varauduttava siihen, että tuloksen suhteellisesta tarkkudesta katoaa cond(A):n suuruusluokan verran merkitseviä numeroita.
   

.

2.5. (elokuu 2010)

Tämän voisit ottaa vaikka tehtävän 2 b-kohdan sijaaan.

Muodosta matriisi A ja vektori b:

           1/2 1/3 1/4         0.95
        A= 1/3 1/4 1/5      b= 0.67
           1/4 1/5 1/6         0.52

1. Ratkaise yhtälö Ax=b
2. Olkoon c vektori, joka saadaan muuttamalla b(3) luvuksi 0.53. Ratkaise yhtälö Au=c. Muuttuiko ratkaisu ja miten paljon?
3. Laske datan ja ratkaisun muutoksen (virheen) normit funktiolla norm jaettuna norm(b):llä ja vastaavasti norm(x):llä. (Siis datan ja ratkaisun suhteelliset virheet.)
4. Muodosta cond(A) ja norm(A)*norm(inv(A)), pitäisi olla samat.
5. Vertaa lukuja cond(A)*(datan suht. virhe) ja ratkaisun suht. virhe. Ovatko samaa suuruusluokkaa?

3.

Piirrä seuraavien funktioiden kuvaajat. Päätä itse sopiva x-väli. Piirtämisen jälkeen voit asetella koordinaatiston halutuksi axis- komennolla. Pelkkää x-aluetta (vast. y-aluetta) voit muutella xlim ja ylim-komennoila. Kokeile!
Muista 1) Pisteittäiset laskutoimitukset, 2) Aloitus: x=linspace(a,b,n); y=f(x); Puolipisteet komentojen lopussa (Jos et muista, niin itket tai ainakin hiljaa kärsit.)

1. exp(-x²)
2. x sin(2x²+1)
3. tan x välillä [-pi/2,9*pi/2]. (Ennen axis- tai ylim-komentoa kuva on varsin epäinformatiivinen.)
4. Sama kuin edellä, mutta hallitummin, ilman (miltei) pystysuoria viivoja ja käyttäen hyväksi tan-funktion jaksollisuutta. Tähän voit hyvin katsoa ratkaisun suoraan C. van Loan - tiedostosta TangentPlot.m Kokeile ja omaksu! Huomaa, että jaksollisen funktion arvoja ei suotta lasketa uudestaan seuraavassa jaksossa.

4.

Tässä harjoitellaan lausekkeen kirjoittamista. Jos jo hyvin osaat, voit mainiosti jättää väliin.
Olkoon

Tämä on exp-funktion rationaaliapproksimaatio, ns. Pade-approksimaatio. Piirrä kuvaaja välillä [0,1].
Aloita vaikka: x=linspace(0,1,200);

Neuvo: Selkeyden vuoksi kannattaa ottaa käyttöön apumuuttujia, kuten osoittaja, nimittaja . Piirrä samaan kuvaan exp-funktio eri värillä ja eri kuvaan erotus f-exp.

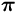5. Monte Carlo-approksimaatio :lle

Pirrä kuva

 t=linspace(0,2*pi);
 x=cos(t);y=sin(t);
 plot(x,y,[1 1 -1 -1 1],[-1 1 1 -1 -1]);
 axis([-1.5 1.5 -1.5 1.5])
 axis square

Heitetään tikkaa kuvan mukaiseen tauluun (tikat osuvat aina taulua ympäröivään neliöön, ehkä tähän oikeasti tarvitaan "satunnaisrobotti"). Jos tikkojen osumatarkuus on satunnaismuuttuja, joka on tasajakautunut neliöllä -1<x<1, -1<y<1, niin ympyrään ja neliöön osuneiden tikkojen lukumäärän suhde on 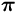/4. (Pinta-alojen suhde.) Generoi tasajakautuneita pistepareja ja laske ko. osuus.

Kirjassa C.vanL on hyvä tiivis selvitys aiheesta "Random processes" 1.3.2 ss. 34 - 37. Jos tämä kiinnostaa, voit lainata kirjaa (luokassa 3 kpl).
Esiintyviä Matlab-funktioita: hist, rand, randn.

Polynomit

5.

Muodosta Matlabilla polynomien p(x)= x3+2x -1 ja q(x)=2x5+ 3 summa ja määritä sen arvo vektorin -1:0.5:1 pisteissä. Piirrä kuvaaja, jossa on p,q ja p+q sopivalla välillä.

6.

Seuraavassa p,q jne ovat vektoreita, jotka edustavat polynomeja (siis polynomien kerroinvektoreita).

1. Kirjoita yleispätevä Matlab-lauseke, joka laskee polynomien p ja q summan. Olkoot p:n ja q:n asteluvut m ja n, oletetaan: m <= n.
2. Kirjoita Matlab-lauseke, joka muodostaa polynomin p derivaatan.
   Vast: Kts. Matlab-funktion polyder koodia. Mutta älä vielä!
3. Muodosta tehtävän 1 polynomien p ja q tulo r funktiolla conv "konvoluutio". Tarkista, päteekö

      polyval(r,x)==polyval(p,x)*polyval(q,x)
   

   missä x on sopiva vektori. Miten monta alkiota x:ssä on oltava, jotta varmuus identtisyydestä saadaan?

7. Ohjelmointitehtävä

Kts. lyhyen oppaan ohjetta.
Myös Matlab: doc -> getting started -> programming -> Scripts and functions
Kirjoita funktio omapolyder, joka muodostaa argumenttina annetun polynomin derivaattapolynomin (siis kerroinvektorin). Lisäksi omapolyder piirtäköön polynomin ja derivaatan kuvaajat samaan kuvaan eri väreillä. Voit valita piirtovälin vaikkapa kiinteästi: [-1,1] (ettei tehdä asiasta liian mutkallista).