Matlab-tehtäviä 3

Ratkaisuja tehtäviin voit kurkistella täältä. Kannattaa toki miettiä ensin itse, toisaalta ei ole syytä jokaiseen tehtävään käyttää liikaa aikaa. Hae itsellesi sopiva etenemistyyli, kunhan otat opiksesi.

1. Jo on korkea aika ratkaista yksi lin. yhtälöryhmä
Olkoon annettu vektorit: 
  >> v1=[-1.996 2.884 -0.03]
  >> v2=[3.10 -2.70 -0.13]
  >> v3=[-1.170 0.70 1.13]
Esitä vektori v=[1 2 3] edellisten lineaarikombinaationa.
Vihje: Lineaarinen yhtälöryhmä syntyy latomalla vektorit sarakkeiksi matriisiin, sillä kerrotaan tuntemattomien kertoimien vektori. Siinä se yhtälöryhmä.
2. Interpolaatio
Muodosta interpolaatiopolynomi pisteistölle, joka saadaan laskemalla funktion f(x)=cos(1+x2) arvot tasavälisessä x-pisteistössä, jossa on 7 pistettä välillä [0,3]. Piirrä samaan kuvaan funktio, datapisteet (rinkuloilla) ja interpolaatiopolynomi. Sinun on tiedettävä, mikä on polynomin asteluku. Tarkistus: Kulkeeko polynomi kaikkien datapisteiden kautta.

3d-grafiikkaa

3.
Suorita joitain alla olevia (tai vastaavia) komentoja. Tutki tarpeen mukaan helpistä. (Tämä kehoitushan pätee aina.) 
  Z=eye(30,30);
  mesh(Z)                     % Paina yläpalkin kiertonuolta ja kiertele kuvaa.
  surf(Z)
  mesh(ones(30,30))
  surfc(rand(20,20))
  mesh(hilb(30))              % Epäjohdonmukaisuus: hilb(30,30) ei toimi.
  contour(hilb(30),100)       % 100 korkeuskäyrää
  contour(hilb(30),0:0.01:.1) % Näitä korkeuksia vastaavat käyrät
  pcolor(rand(30,30))
  pcolor(eye(30,30))
  cs=contour(peaks);  % peaks on &matlab;:n mukana tuleva testausfunktio,
  clabel(cs)          % kts. help peaks, type peaks, doc peaks
  clabel(cs,'manual') % Vie hiiriosoitin grafiikkaruutuun ja valitse.
4. Pinta ja korkeuskäyrät (Hig-Hig s. 102-103)
Olkoon
f(x,y)=sin(3y - x2+1)+cos(2y2-2x). Piirrä pintakuva ja korkeuskäyräpiirros, jälkimmäinen sekä contour että ezcontour-funktioilla. Tässä on mahdollisuus kokeilla yllä esiteltyjä korkeuskäyrien valitsemistapoja, myös clabel. Ota alueeksi vaikka [-2 2 -1 1] .
5. Pintapiirto napakoordinaateissa
Piirrä funktion f(x,y)=sin(π(x2 y2)) pintakuva yksikkökiekon päällä. Pyörittele kuvaa.
Neuvo: Lue lyhyestä oppaasta tästä

Ohjelmointia, approksimointia, Taylor

6. Exp-funktion Taylorin sarja
CV-viitteessä on seuraava koodi: 
  function y = MyExpW(x)
% y = MyExpW(x)
% x is a scalar and y is a Taylor approximation to exp(x).
y = 0;
term = 1;
k=0;
while abs(term) > eps*abs(y)
   k = k + 1;
   y = y + term;
   term = x*term/k;
end
Talleta se tiedostoon MyExpW.m . Suorita MATLAB-komento help MyExpW

Muistathan:

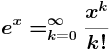exp(x)=...     (Jostain syystä summa-merkki ei "tarttunut".)

Selvitä, mitä koodi tekee ja testaa kutsumalla sitä eri x:n arvoilla. (Mikä on eps ?)

7. Taylor exp, vektoriversio
Edellinen skalaariversio ei ole tyypillistä MATLAB-ajattelua, vaan valmistelua oikeaoppisemmalle vektoriversiolle.
Kirjoita m-tiedosto: omaexp.m täydentäen alla olevaa: 
  function y=omaexp(x)
% y=omaexp(x)   % Funktion kutsu 
% x on vektori, y on samanpituinen vektori, y(i)=Texp(x(i)),
%   missä Texp tarkoittaa Taylor-approksimaatiota.
% Esim: 
%       x=linspace(-1,1); y=omaexp(x); plot(x,y)
y=zeros(size(x));  % Alustus, ei välttämätön, mutta tehostaa.
termi=ones(size(x)); % Sarja alkaa 1:stä, olipa x(i) mikä tahansa.
k=0;
while(any(abs(termi) > eps*abs(y))
  y=...
  k=...
  termi= ...
end
Selvitä itsellesi, täydennä, suorita, piirrä.
Vastaus: MyExp4
8. Newtonin menetelmä
Seuraava koodi toteuttaa Newtonin menetelmän epälineaariselle yhtälölle: 
k=0;xedell=-Inf;
while abs(x-xedell) > eps*abs(x)
    xedell=x;
    x=x-f(x)/fder(x);
    k=k+1;
end
Täydennä tämä funktioksi tiedostoon myNewton.m. Otsikkorivi:
function z=myNewton(f,fder,x)
Kirjoita helppiteksti. Muista, että funktion paluumuuttujalle z pitää sijoittaa lopullinen arvo.
Testaa aluksi vaikka tyyliin
myNewton(@sin,@cos,2)