Matlab-tehtäviä 1

Ratkaisuja täällä.
1.
Määrittele vektorit 
  x = [1 2 3 4 5]
  y = [0 2 4 6]
  z = [-4 -2 0 2 4 ]

Kokeile seuraavia laskutoimituksia edellä määriteltyihin muuttujiin. 

   x.*z , x'*z , x*z'  x*z  % miksi virhe ?
   sqrt(x*x'), norm(x)      % Miksi sama tulos?
   x.^2  ,  x^2
2.
Määrittele seuraavat matriisit: 
       3           0
   u = 4       v = 2
       5           4
       6           6
       1  2  3        1  2  3  4        3  4  5  6
   c = 1  3  6    a = 5  6  7  8    b = 2  1  0 -1
       1  4  9        9 10 11 12        5  4  2  0
                                        1  2  1  1
Kokeile 
   a*c   c*a    c^2    c.^2   a^2    a.^2
3.
Tutustu helpin avulla funktioihin: eye, ones, zeros, diag ja size. Olkoon Yn×k sellainen matriisi jonka kaikki alkiot ovat ykkösiä ja jonka koko on n×k. Vastaavasti olkoon Nn×k nollamatriisi ja In×n yksikkömatriisi. Muodosta seuraavat matriisit
/\
|In×n Yn×k|
| |
|Nk×n Ik×k|
\/
 
/\
|Nnxn Inxn|
| |
|-Inxn Nnxn|
\/
kun n=4 ja k=3.
3.5
  1. Miten kääntäisit vektorin v alkiot vastakkaiseen järjestykseen kaksoispisteen (:) avulla?
  2. Entä matriisin A sarakkeet, vastaavasti rivit?
    (Näihin on myös valmiit funktiot: fliplr ja flipud, "LeftRight, UpDown")
  3. Miten limität ("merge") kaksi samanpituista vektoria u ja v ?
    Vihje: Liitä vektorit allekkain ja jonouta näin saatu matriisi sarakkeittain. Nokkelaa!
4.
Taikaneliön saa komennolla magic(n) . Muodosta (pienehköllä n) matriisin M=magic(n) rivisummat, sarakesummat, lävistäjäsumma ja sivulävistäjäsumma.
Laske taikaneliösi ominaisarvot ja -vektorit (eig). Miten voisit suoraan päätellä suurimman ominaisarvon ja vastaavan ominaisvektorin?

Taikaneliöillä on mielenkiintoinen historia. Ne tunnettiin Kiinassa 2000 vuotta e.a.a. Kts. Molerin kirjan introsta s. 18 alk. Myös Matlab:n dokumentaatiosta.

5.
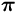Piirrä yksikköympyrä käyttäen parametriesitystä x=cos(t), y=sin(t), t välillä [0,2pi]. Siis tähän tapaan: 
» t=linspace(0,2*pi);x=cos(t);y=sin(t);plot(x,y)
» axis equal;axis square

Miten piirtäisit säännöllisen 10-kulmion?

6. Taikaneliöjatkot
Aloita tähän tapaan: 
A=magic(5)
A=A*ans
    % Jatka nuolinäppäiniteroinita.
Mitä havaitset? (Voitaisiin laskea myös suoraan matriisin potensseja: A^k, mutta peräkkäin kertominen kertoo enemmän (!))
Suorita eig ja inv-funktioiden avulla A:n diagonalisointi: 
              A = VDV-1
Selitä ilmiö tämän avulla. Laske ensin Dk. (Voit tehdä sen korottamalla diagonaalivektorin potenssiin k, tee mieluummin tällä, laskutoimituksia säästävällä tavalla, samalla saat harjoitusta diag-komennon käytöstä.)
Kerro sitten DkV-1. Eiköhän nyt ala valjeta!
Huom! Tätä käytöstä varten ei tarvita taikaa kokonaisuudessaan, rivisummien samuus riittää. (Muistele Markovin matriiseihin liittyviä tehtäviä 3-peruskursseilla, jos tämä on ensi tutustuminen, muistele tätä sitten perästäpäin.)
Tehtävät 2