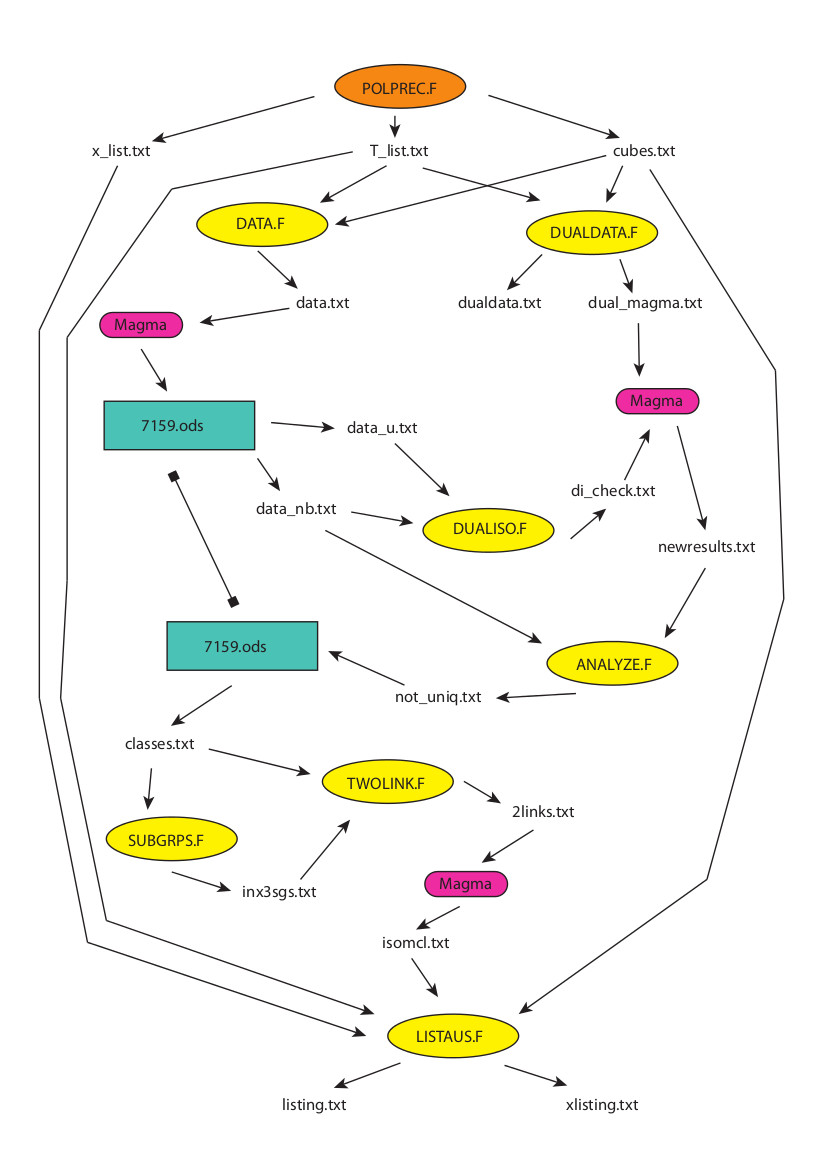
Data & scripts for triangular hyperbolic buildings projects
This page explains step by step how the results in the paper Groups acting simply transitively on vertex sets of hyperbolic triangular buildings by Carbone, Kangaslampi and Vdovina are calculated, using several Fortran90 scripts and Magma.
Disclaimer: The project is a mess and the scripts are beyond ugly, reading them is not recommended for anyone. Maybe some day I will clean everything up and write the whole project into an understandble C-program, but in the meanwhile, here it is in its original form.
List of scripts in order of appereance:
List of data files in order of appeareance:
- T_list.txt
- x_list.txt
- cubes.txt
- data.txt
- 7159.ods = the groups in a table
- dualdata.txt
- dual_magma.txt
- data_u.txt
- data_nb.txt = list of groups in order by abelinizations
- di_check.txt
- di_magma.txt = catenation of dual_magma.txt and di_check.txt
- newresults.txt = Magma results for di_magma.txt
- not_uniq.txt
- classes.txt
- inx3sgs.txt
- 2links.txt
- isomcl.txt
- listing.txt
- xlisting.txt
polprec.f
Uses subroutines nxtprm.f and echeck.f.
POLPREC searches triangle presentations for a one-vertex polyhedron having the smallest thick generalized quadrangle GQ(2,2) as the vertex-link. POLPREC searches only those presentations, which have at least one cubic triangle (xj,xj,xj). This is done by going through all possible ways to label the rows of a given matrix (containing permutations of S_6) to obtain incidence tableaus. Each incidence tableau in turn gives a triangle presentation. POLPREC gives as a result one representative of each equivalence class of triangle presentations.
Output:
T_list.txt (list of triangles)
x_list.txt (list of permutations giving incidence tableaus)
cubes.txt (number of cubic triangles in each presentation)
data.f
Writes the results of POLPREC into a file, which can be run in Magma to calculate the abelinizations and abelinizations of all index 3 subgroups.
Input: T_list.txt, cubes.txt
Output: data.txt (Magma file to calculate abelinizations for the groups and its all index 3 subgroups)
dualdata.f
Creates the duals groups from the triangle groups.
For each group considered creates the dual group and as output gives a file that can be run in Magma to calculate which of these dual groups are isomorphic.
Input: T_list.txt, cubes.txt
Output:
dualdata.txt (duals as list)
dual_magma.txt (duals in Magma format)
*****************************************************************
At this point the results obtained by running data.txt in Magma are opened on a spreadsheet 7159.ods, and ordered "alphabetically" by abelinizations. We know that groups having different abelinization, or different index 3 subgroups, cannot be isomorphic. So when checking the isomorphism of the groups we only need to compare each group to those that have same abelinization and same set of abelinizations of the index 3 subgroups. We save the order of groups to file data_nb.txt and the numbers indicating which groups to compare to data_u.txt.
******************************************************************
dual_iso.f
Given list of which groups might be isomorphic and which not, creates a file that can be run in Magma 5together with the dula data file dual_magma.txt) to decide, if the duals are isomorphic or not.
Input: data_u.txt, data_nb.txt
Output: di_check.txt (Magma code to calculate isomorphisms)
*****************************************************************
Now we glue the file di_check.txt to the end of dual_magma.txt and run the obtained file with Magma. As a result we get file newresults.txt which tells which groups are isomorphic.
*****************************************************************
analyze.f
Analyzes the given magma data about isomorphic dual pairs. Prints a list of numbers to be pasted into the spreadsheet 7159.ods that indicate whether each group is unique or not.
Inputs: data_nb.txt, newresults.txt
Output: not_uniq.txt (to be pasted into 7159.ods)
*****************************************************************
Paste not_uniq.txt into 7159.ods. Now we can pick up a list of representatives, one presentation for each non-isomorphic group of presentations. Save this list to classes.txt.
*****************************************************************
subgrps.f
Creates the three covers of each given group for twolink.f.
Input: T_list.txt, cubes.txt, classes.txt
Output: inx3sgs.txt
twolink.f
Calculates the links of radius 2 of the triangle presentations (of index 3 subgroups of the cases with torsion) given as input. Outputs the adjacency matrices of the two-links in a form that can be inputted to Magma.
There are 45 labels in the triangles. We denote them as follows:
incoming 1 = 1
outgoing 1 = 2
incoming 2 = 3
outgoing 2 = 4
incoming 3 = 5 etc.
The 2-link is calculated around that vertex which has incoming edge with the label 1. In that vertex, the incoming edges have labels 3k-2 and outgoing edges of with labels 3k. The 2-link is calculated starting with the neighbour along incoming 1, then outgoing 3, incoming 4, outgoin 6 and so on. We calculate the 1-links at the neighbouring vertices, then remove and add certain edges in/between the 1-links to obtain 2-link. The result is a graph with 780 vertices, all of index 3 (30 x part of 1-link + additional edges between these).
Input: inx3sgs.txt, classes.txt
Output: 2links.txt
***************************************************************
Run the file 2links.txt in Magma to see, which groups have 2-links isomorphic to the first and which to the second presentation. This devides the presentations into two set: as covering spaces there are two different buildings with these two different 2-links.
*****************************************************************
listaus.f
Lists the non-isomorphic presentations together with a number indicating the type of the 2-link, in tex-format for the article. listing.txt lists the triangle presentations, xlisting.txt lists the permutations giving these presentations.
Input: T_list.txt, cubes.txt, x_list.txt, classes.txt, isomcl.txt
Output: listing.txt, xlisting.txt