Exponenttifunktion Taylorin polynomeja (mlGr10D.m)
mlGr10D.m
https://math.aalto.fi/opetus/Mattie/Blogi/Matlab/html/ExpTaylor.html
Contents
close all % Suljetaan mahd. avoinna olevat % grafiikkaikkunat x = [-2:.01:2]; % Diskreetti x-akselin väli y = exp(x); % exp-funktion arvot x-pisteissä
Lasketaan Taylorin polynomien arvoja x-pisteissä
p0 = ones(size(x)); % Ykkösistä koostuva vektori p1 = p0 + x; % Lisätään x-vektori p2 = p1 + (x.^2)/2; % Seuraava termi, huomaa .^ p3 = p2 + (x.^3)/6; % Ja vielä yksi.
Piirretään kaikki samaan kuvaan
plot(x,y) hold on plot(x,p0) plot(x,p1) plot(x,p2) plot(x,p3) grid on legend('e^x','p0','p1','p2','p3','Location','NW') % NW=North West shg % "Show Graphics" Ei välttämätön, mutta hyvä.
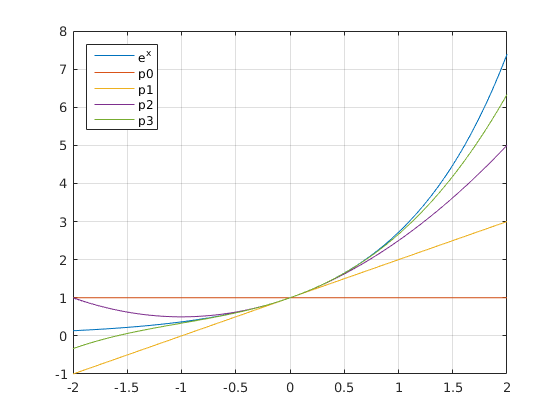
Entä, jos halutaan laskea ja piirtää korkeamman asteisia?
Otetaan käyttöön for-silmukka, tehdään alusta saakka:
p{1}=ones(size(x)); % Matlab ei salli 0-indeksiä. Huomaa aaltosulut {}.
% p{k} voidaan ajatella indeksoituna (vektori)muuttujana.
N=10; % Muuttele tarpeen mukaan
for k=1:N
p{k+1}=p{k}+(x.^(k))/factorial(k);
end
% plot(x,y,x,p{4},x,p{6},x,p{8},x,p{10}) % Nyt plot:n muoto, jossa monta
% kuvaajaa samalla komennolla.
% grid on
% shg
% Jätettiin kommenttien taakse, selvennetään laittamalla värimääreitä:
% 'r' = red, 'g'=green, 'k'=black
hold off % Seuraavat piirtokomennot pyyhkivät edelliset piirroket plot(x,y,'r--',x,p{3},'g',x,p{5},'b',x,p{9},'k') % Parilliset polynomit hold on % Pidetään edelliset plot(x,y,'r--','LineWidth',2) % Punainen, paksumpi katkoviiva, jotta % erottuisi seuraavassa p{9}:n kuvaajasta. grid on title('e^x ja parillisia Taylorin polynomeja') legend('e^x','T_2','T_4','T_8','Location','NW') shg % % Zoomaamalla gragfiikkaikkunaa suurennuslasilla nähdään, missä vaiheessa % T_8 :n (eli p{9}:n) ja exp(x).n kuvaajat erkanevat. %
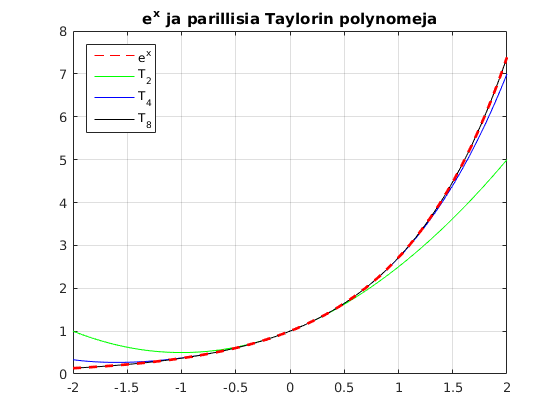
Approksimointivirhe
figure % Avataan uusi grafiikkaikkuna. plot(x,y-p{9}) % Piirretään erotus exp(x)-T8(x) title('Virhe: e^x - T_8(x)') grid on shg
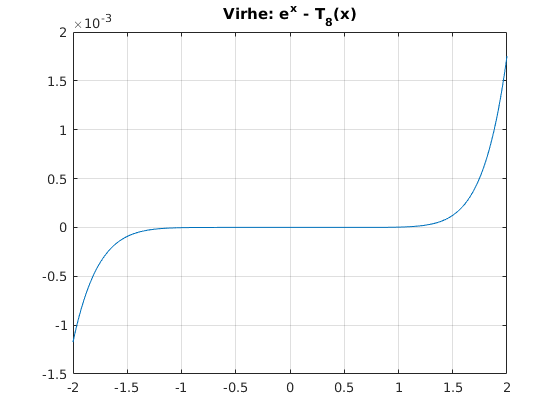
Ja lasketaan maksimivirhe:
maksvirhe=max(abs(y-p{9}))
%
maksvirhe =
0.0018