Työssä käydään läpi lokaalin röntgentomografian matemaattista teoriaa.
Tämä teoria osoittaa, milloin ja miten n-ulotteinen kappale (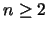 )
voidaan rekonstruoida käyttämällä mittaustuloksia siitä, kuinka paljon
röntgensäteet vaimenevat kappaleen läpi kulkiessaan.
Matemaattisesti kyse on kompaktikantajaisen funktion )
voidaan rekonstruoida käyttämällä mittaustuloksia siitä, kuinka paljon
röntgensäteet vaimenevat kappaleen läpi kulkiessaan.
Matemaattisesti kyse on kompaktikantajaisen funktion
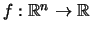 määrittämisestä sen integraaleista eri suoria pitkin. määrittämisestä sen integraaleista eri suoria pitkin.
Itse funktion f rekontruktio on numeerisesti epästabiili toimitus,
mutta työssä johdetaan lähteen [SK] mukaisesti kaavat,
joiden avulla e * f ja
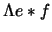 voidaan rekonstruoida stabiilisti.
Tässä e * f ja
voidaan rekonstruoida stabiilisti.
Tässä e * f ja
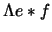 ovat eräiden oletusten vallitessa
funktioiden f ja
ovat eräiden oletusten vallitessa
funktioiden f ja
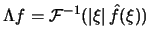 approksimaatioita, joissa pienimmät yksityiskohdat ovat sumentuneet.
Rekonstruktiokaavoja johdettaessa tarvittavaa
Calderón-Zygmund-teoriaa käydään myös läpi,
pitkälti teoksen [Ner] esitystapaa seuraten.
approksimaatioita, joissa pienimmät yksityiskohdat ovat sumentuneet.
Rekonstruktiokaavoja johdettaessa tarvittavaa
Calderón-Zygmund-teoriaa käydään myös läpi,
pitkälti teoksen [Ner] esitystapaa seuraten.
Funktio 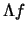 antaa käyttökelpoista tietoa kappaleen
sisäisestä rakenteesta,
sillä Calderónin pseudodifferentiaalioperaattori
antaa käyttökelpoista tietoa kappaleen
sisäisestä rakenteesta,
sillä Calderónin pseudodifferentiaalioperaattori 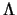 säilyttää epäjatkuvuuskohtien sijainnin.
Tämä osoitetaan
lähteestä [RK] löytyvän hahmotelman mukaisesti
näyttämällä, että funktioiden f ja säilyttää epäjatkuvuuskohtien sijainnin.
Tämä osoitetaan
lähteestä [RK] löytyvän hahmotelman mukaisesti
näyttämällä, että funktioiden f ja 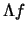 aaltorintamajoukot ovat samat.
Todistuksessa ei tarvita pseudodifferentiaalioperaattoreiden
teoriaa. aaltorintamajoukot ovat samat.
Todistuksessa ei tarvita pseudodifferentiaalioperaattoreiden
teoriaa.
Eräs syy funktion 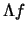 tarkastelemiseen on, että
sen likimääräinen rekonstruktio onnistuu paikallisesti:
jos kiinnostuksen kohteena on vain osa kappaleesta,
rekonstruointia varten tarvitaan mittaukset ainoastaan niitä suoria pitkin,
jotka kulkevat kiinnostavan alueen läpi tai aivan sen läheltä.
Funktioita f ja e * f ei voida rekonstruoida paikallisesti.
tarkastelemiseen on, että
sen likimääräinen rekonstruktio onnistuu paikallisesti:
jos kiinnostuksen kohteena on vain osa kappaleesta,
rekonstruointia varten tarvitaan mittaukset ainoastaan niitä suoria pitkin,
jotka kulkevat kiinnostavan alueen läpi tai aivan sen läheltä.
Funktioita f ja e * f ei voida rekonstruoida paikallisesti.
Kaksi stabiilisuustulosta, joita ei ole suoraan esitetty kirjallisuuslähteissä,
todistetaan myös. Niiden mukaan mittausvirheen L2-normi rajoittaa
tasaisesti funktioiden e * f ja
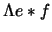 rekonstruktioiden virheitä.
rekonstruktioiden virheitä.
Lukijalta edellytetään reaalianalyysin, distribuutioteorian ja
Fourier-analyysin perustietoja;
näiden keskeisimpiä kohtia luetellaan liitteessä.
Työssä esitetään todistukset kaikille tuloksille, joita
käytetään teorian johtamisessa,
lukuunottamatta edellä mainittuja esitietoja sekä
kahta Rieszin muunnosten jatkuvuutta koskevaa lausetta,
joiden osalta viitataan lähteeseen [Zie].
Näistä lauseista seuraa myös se, että lähteessä [SK]
esiintyvä funktioavaruus
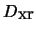 onkin itse asiassa vain
neliöintegroituvien funktioiden avaruus.
Tästä seikasta ei löydy mainintoja aikaisemmassa kirjallisuudessa.
onkin itse asiassa vain
neliöintegroituvien funktioiden avaruus.
Tästä seikasta ei löydy mainintoja aikaisemmassa kirjallisuudessa.
|
![[Up]](http://www.math.hut.fi/gadgets/trup.gif)
![[English]](/gadgets/eng.gif)