This thesis provides a self-contained account of the basic mathematical theory
of local x-ray tomography.
The theory shows when and how an n-dimensional object (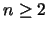 )
can be reconstructed,
using attenuation measurements of x-rays passing through the object.
Mathematically speaking, the problem is to determine
a compactly supported function )
can be reconstructed,
using attenuation measurements of x-rays passing through the object.
Mathematically speaking, the problem is to determine
a compactly supported function
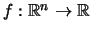 from its line integrals.
from its line integrals.
The reconstruction of f itself is a numerically instable operation,
but formulae are derived for the stable reconstruction of
e * f and
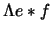 ,
following [SK].
Here e * f and ,
following [SK].
Here e * f and
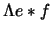 are, under certain assumptions,
blurred approximations of f and
are, under certain assumptions,
blurred approximations of f and
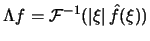 ,
respectively.
The Calderón-Zygmund theory
needed for deriving the reconstruction formulae
is also presented, largely according to [Ner]. ,
respectively.
The Calderón-Zygmund theory
needed for deriving the reconstruction formulae
is also presented, largely according to [Ner].
The function 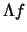 provides meaningful information about
the internal structure of the object,
since the Calderón pseudodifferential operator
provides meaningful information about
the internal structure of the object,
since the Calderón pseudodifferential operator 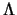 preserves the locations of discontinuities.
This is shown by proving that the wave front sets of
f and preserves the locations of discontinuities.
This is shown by proving that the wave front sets of
f and 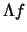 are the same.
The elementary proof of this fact, which does not use the theory of
pseudodifferential operators, is presented as outlined in
[RK].
are the same.
The elementary proof of this fact, which does not use the theory of
pseudodifferential operators, is presented as outlined in
[RK].
One reason for considering 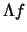 is that
its approximate reconstruction can be done locally.
This is to say that if the region of interest is only part of the object
examined, measurements are needed only along lines
through the region of interest, or very close to it.
The functions f and e * f cannot be reconstructed locally.
is that
its approximate reconstruction can be done locally.
This is to say that if the region of interest is only part of the object
examined, measurements are needed only along lines
through the region of interest, or very close to it.
The functions f and e * f cannot be reconstructed locally.
Two stability results not directly given in the references are proved.
They state that the errors in the reconstructed e * f and
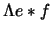 are uniformly bounded by the L2 norm of the error in the measurements.
are uniformly bounded by the L2 norm of the error in the measurements.
The presentation is self-contained in the sense that
only some basic knowledge of real analysis, distribution theory and
Fourier analysis is required;
some of the most central results of this background theory
are listed in an appendix for reference.
Apart from these prerequisites, proofs of all results used are given,
except for two theorems concerning
the continuity of the Riesz transform,
for whom the reader is referred to [Zie].
These theorems also imply that the function space
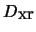 ,
considered in [SK],
is just the space of square-integrable functions.
Earlier statements of this fact were not found in literature. ,
considered in [SK],
is just the space of square-integrable functions.
Earlier statements of this fact were not found in literature.
|
![[Up]](http://www.math.hut.fi/gadgets/trup.gif)
![[Finnish]](/gadgets/fin.gif)