MATLAB-opas

Grafiikka

MATLAB sisältää monipuoliset piirtokomennot datan 2- ja 3-ulotteiseen visualisoimiseen. Katso esimerkiksi komentoja plot ja plot3.

Käyrien piirtäminen

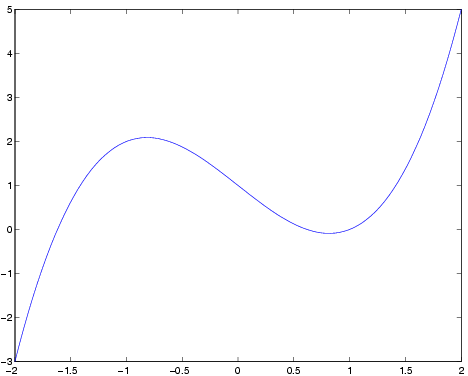
Käyriä voi piirtää plot-komennon avulla. Ajatellaan, että haluamme piirtää käyrän y=x³-2x+1 välillä [-2,2]. Näin se käy: Muuttujaksi x otetaan sataan osaan diskretoitu x-akseli.

» x=linspace(-2,2,100);

Luvun 100 voi jättää pois, sillä 100 on oletusarvo. Lasketaan y-vektoriin vastaavat funktion arvot. Huomaa .^ (mieti tarkkaan pisteen merkitys).

» y=x.^3-2*x+1;

komento

» plot(x,y)

piirtää x-vektorin ja y-vektorin vastinkomponenttien ilmaisemat koordinaattipisteet (x(i),y(i)), ja yhdistää ne välijanoilla. Kun pisteitä on tarpeeksi (usein 100 riittää), saadaan sileä käyrä kuvaksi.

Kokeile minkälaisen käyrän saat jos 100:n sijasta käytät arvoa 10.

Kuvan skaalausta voi muuttaa komennolla axis. Perusmuoto on axis([xmin xmax ymin ymax]), joka määrää koordinaatiston rajat. axis-komennon argumenttina voi olla myös erinäisiä merkkijonoja, joista useimmin tarvittavia lienevät axis('equal') ja axis('square'). Alkutilaan päästään komennolla axis('normal').

axis('equal') ja axis('square'), jotka muuten voi antaa myös tyyliin axis equal, ovat erityisen tarpeellisia silloin, kun halutaan esim. ympyrän näyttävän ympyrältä.

Kokeile miten äsken saamasi kuva muuttuu kun käytät yllä mainittuja axis-komennon eri muotoja. Kuvaa voi käsitellä kuvaikkunan työkalunauhan valikosta näkyvillä tavoilla. Sitä voi "zoomata" (suurennuslasi), kuvaan voi lisätä tekstejä (insert-valikosta "text") jne. Samoja asioita voi hoitaa myös komennoilla, kuten zoom on.

Jos haluat piirtää toisen käyrän jo olemassaolevaan kuvaan, niin anna komento hold on. Tämän jälkeen kaikki seuraavat käyrät tulevat edellisten 'päälle', kunnes annetaan komento hold off. Piirrä yllä saadun käyrän kanssa samaan kuvaan y=2cos(x²-5x+17).

Toinen tapa usean käyrän piirtämiseksi samaan kuvaan on plot-komennon muoto plot(x1,y1,x2,y2,x3,y3,...). plot-komennossa voi lisätä viivatyyppimääreen kullekin haluamalleen käyrälle. Jos haluttaisiin vaikkapa piirtää sinikäyrä sinisellä, kosinikäyrä katkoviivalla ja lisäksi merkitä jälkimmäiselle rinkuloilla kaikki /2:n monikerrat välillä [0,10], olisi sopivaa tehdä näin:

» x=linspace(0,10);
» x1=0:pi/2:10;
» plot(x,sin(x),'b',x,cos(x),'--',x1,cos(x1),'o')
» grid

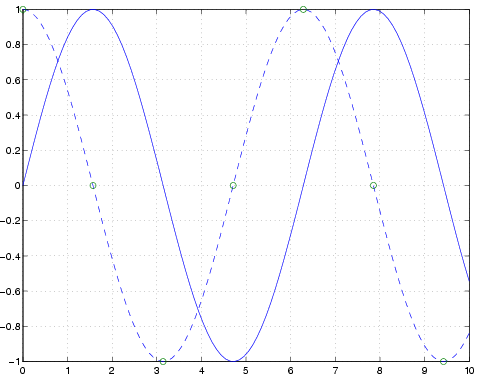
Huom 1: plot(x1,cos(x1),'o') ('o' :n sijalla käy esim. 'x' tai '.') piirtää vain ao. pisteet, mutta jättää yhdistysjanat piirtämättä.

Huom 2: Yleinen muoto on plot(x1,y1,'mjono1',x2,y2,'mjono2',x3,y3,...), missä 'mjono1', 'mjono2',... ovat yllä esiintyvän tyylisiä merkkijonoja, joilla ilmaistaan väri tai viivatyyppi. Argumentit voidaan mieltää kolmikoiksi, yksi kolmikko kutakin piirrettävää käyrää kohti. Mistä tahansa kolmikosta voidaan jättää merkkijono-osa pois, jolloin ko. käyrä piirretään oletusvärillä ja -tyypillä.

Komennollagrid- voidaan kuvaan lisätä koordinaatti- (hila-) viivat, mikä on usein hyödyllistä. Kokeile joitakin yllä esitetyn kaltaisia yhdistelmiä.

Uuden piirtoikkunan saa avatuksi komennolla figure. Piirtoikkunoilla on numero, jonka avulla useista ikkunoista voidaan valita se, johon halutaan piirtää: komento figure(n), missä n on ikkunan numero, ohjaa seuraavat käyrät ikkunaan n.

Piirtämishuomioita

Funktiossa linspace on oletusarvona jako sataan osaan, mikä on usein sopiva 2D-piirroksiin. Tavallisimmin piirto tehdään siten tähän tapaan:

» x=linspace(a,b); % a:lla ja b:llä oltava numeeriset arvot.
» y=lauseke;

Lauseke, jossa esiintyy x, kuten y=exp(sin(x))+x.^3;

» plot(x,y)

Toinen tapa x-diskretointiin on antaa jakovälien lukumäärän sijasta jakovälin pituus h, jolloin kirjoitettaisiin
>> x=a:h:b;

Yllä kannattaa panna merkille puolipisteen käyttö, joka säästää tarpeettomalta pitkän vektorin tulostukselta.

Funktion piirto, fplot

fplot on vaihtoehtoinen tapa funktion piirtämiseen. Tällöin funktion on oltava joko MATLAB-funktio (kuten sin, cos, exp, ...) tai itse määritelty funktio (joko m-tiedosto tai ns. "inline"-määrittely). Versiossa 6 sallitaan myös Matlab-lauseke, jossa esiintyy yksi muuttuja.

Esim: fplot('sin',[0,2*pi]) tekee saman kuin x=linspace(0,2*pi);plot(x,sin(x)). Erona on se, että fplot suorittaa ns. adaptiivisen diskretoinnin, joka mahdollistaa tarkan kuvan vähemmällä laskentatyöllä.
Esim: Määrittelemme funktion ns. "inline"-tavalla.

>> f=inline('x.^2','x')
f =
     Inline function:
     f(x) = x.^2
>> fplot(f,[0,1])

Näinkin yksinkertaisesti voidaan menetellä: fplot('x.^2',[0,1])

Tämä toimii sillä filosofialla, että merkkijono 'x.^2' on merkkijonona annettu Matlab-lauseke, jossa esiintyy vain yksi muuttuja. Tällöin Matlab ymmärtää sen tässä yhteydessä tämän yhden muuttujan funktioksi.

Saman filosofian mukaisesti myös inline-määrittely voidaan kirjoittaa lyhyemmin muodossa
>> f=inline('x.^2') , mikäli siinä esiintyy vain yksi muuttujasymboli.

Parametrimuotoiset käyrät tasossa

Funktio plot soveltuu sellaisenaan parametrimuotoiseen piirtoon. Ajatellaanpa yksinkertaisimpana esimerkkinä ympyrää, jonka luonnollinen parametriesitys on x=cos(t), y=sin(t), t [0,2].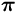

>> t=linspace(0,2*pi);
>> x=cos(t); y=sin(t);
>> plot(x,y)
>> axis equal; axis square;

3D-grafiikka

Avaruuskäyrät

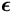Parametrimuodossa annettuja avaruuskäyriä voidaan piirtää funktiolla plot3 lisäämällä z-koordinaatti mukaan. Esimerkki selvittäköön asian. Jatketaan parametripiirtoesimerkkiä ottamalla mukaan z-koordinaatti, joka nousee lineaarisesti kulman t funktiona. Toisin sanoen piirrämme ruuviviivan: x=cos(t), y=sin(t), z=t, t [0,6]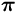

>> t=linspace(0,6*pi);
>> x=cos(t); y=sin(t); z=t;
>> plot(x,y,z)
>> axis equal; axis square;
>> grid

Tämä on periaatteessa sama esimerkki kuin funktion plot3 avustussivulla. Kuvakin näkyy siellä (tosin hiukan eri parametrein).

Pintapiirrokset ja korkeuskäyrät

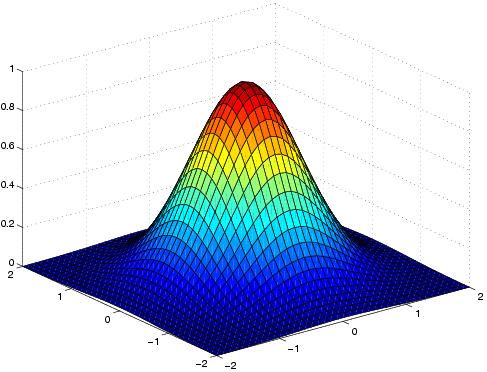
Olkoon piirrettävänä funktion f(x,y)=e^-x²-y² määrittelemä pinta(pala) xy-tason neliön [-2,2] x [-2,2] alueella. Ajatus on, että jaetaan alue koordinaattiviivoilla suorakulmiohilaksi ja lasketaan kussakin hilapisteessä (x_i, y_j) funktion arvo z_i,j=f(x_i, y_j). Näin saadaan korkeusmatriisi Z=(z_i,j). Ajatellaan, että asetetaan kuhunkin hilapisteeseen (x_i, y_j) sauva, jonka (merkillä varustettu) pituus on z_i,j. Näin syntyneen "sauvametsän" päällee asetetaan lepäämään "pintamatto".

Sama korkeusmatriisi soveltuu niin pinta- (surf), korkeuskäyrä- (contour) kuin yhdistelmäkuviin (surfc).

» x=-2:.1:2; y=x;       % x-ja y-akselin diskretoinnit tässä samoja.
» [X,Y]=meshgrid(x,y);  % X ja Y määräävät xy-alueen hilapisteistön.
» size(X), size(Y)
ans =
    41    41
ans =
    41    41

» Z=exp(-X.^2-Y.^2);   % Korkeusmatriisin arvot hilapisteissä. 
                       % Huomaa "pisteittäiset" laskutoimitukset.
» surf(X,Y,Z)          % surf-funktio "asettaa maton
                       % sauvametsän päälle".

Demonstroidaan view-komentoa:

» for j=1:5;view(-20+10*j,20*j),pause,end;

Kuvan pyörittäminen käy vuorovaikutteisemmin kuvaikkunan työkalunauhan oikeanpuolimmaisesta painikkeesta.

Korkeuskäyräpiirros

» contour(X,Y,Z)

Tehtäviä 2

[Edellinen] [Seuraava] [Alkusivu]