Osa 2. Matriisityöskentelyä |
Kertolasku (*) on nimenomaan matriisikertolasku. Jos halutaan laskea kahden samankokoisen matriisin (vektorin) tulo vastinalkioittain (pisteittäin), kirjoitetaan kertomerkin eteen pite (.).
Jakolasku A\B tai A/B tarkoittaa matriisioperaationa yhtälöryhmän ratkaisemista ja taulukko-operaationa (A./B) yksinkertaisesti vastinalkioittain tapahtuvaa jakoa. (Taulukkotapauksessa A.\B on sama kuin A./B) .
Potenssiin korotus A^p tarkoittaa matriisioperaationa tuloa A*A*...*A ja edellyttää siten, että A on neliömatriisi. Taulukko-operaatio A.^B tarkoittaa vastinalkioittain muodostettuja potensseja ja edellyttää samankokoisia matriiseja (joista toinen voi olla skalaari). Kokoamme taulukkoon:
Matlabin laskutoimitukset
|
Oikeanpuoleiset taulukko-operaatiot suoritetaan siis aina vastinalkioittain ja ne edellyttävät, että operandimatriisit ovat samankokoiset. Jos toinen operandi on skalaari (1 x 1 - matriisi), niin tätä samaa skalaaria käytetään operandina jokaisessa laskutoimituksessa. (Taulukko-operaatioiden kohdalla voidaan ajatella, että Matlab laajentaa skalaarin samankokoiseksi vakiomatriisiksi toisen operandin kanssa.)
Vasemman sarakkeen matriisioperaatiot edellyttävät, että operandit ovat oikean kokoisia kyseiseen toimitukseen. Tässäkin tapauksessa skalaarilla operoiminen onnistuu aina. On syytä huomata, että potenssiin korotuksessa ja jakolaskussa matriisi- ja taulukko-operaatiot eivät ole samoja, vaikka toinen argumentti olisi skalaari. Kertolaskussa sensijaan skalaarin ja matriisin tulo on sama kuin pisteittäinen tulo.
>> x=A\bsaamme lineaarisen yhtälösysteemin A*x = b ratkaisuvektorin x . Kyseessä on neliömatriisin A tapauksessa sama asia kuin laskussa
>> x=inv(A)*bTosin käänteismatriisilla kertominen on numeerisen laskennan tehokkuuden ja tarkkuuden kannalta epäedullisempaa.
Tässä b:n on oltava A:n sarakkeen pituinen sarakevektori tai matriisi, jossa tällaisia sarakevektoreita on ladottuna vierekkäin.
Muistisäänöt:
Mainittakoon vielä, että matriisijakolaskussa A:n ei tarvitse olla neliömatriisi. Ellei se ole, ratkaisu suoritetaan PNS-mielessä. (Palataan lähemmin.)
Toisin kuin Maplessa, Matlabissa ei voida käsitellä "vapaita" muuttujia.Jos käytetään lisäpakkausta "symbolic toolbox", voidaan suorittaa myös symbolisia operaatioita, mutta tässä käsittelemme vain Matlabin perusajatusmaailmaa.
>> x=[-2,-1,0,3,5]
>> x2=x.^2 % x-vektorin 2. potenssit.
>> x^2 % Matriisipotenssi on tuomittu epäonnistumaan.
>> x.*exp(x) % exp toimii "pisteittäin", kerrotaan exp-arvot
% pisteittäin x-arvoilla.
>> x=linspace(-1,2); % 100-pituinen diskretoitu x-akselin pätkä.
>> plot(x,x.*exp(x)) % Yhdistetään kuvaajan 100-pistettä pikku janoilla.
Tee itsellesi selväksi pisteittäiset, vastinalkioittain toimivat operaatiot.
Matriisilausekkeita , vaikkapa matriisipolynomeja voidaan muodostaa, kunhan matriisit ovat kertomiskelpoisia, polynomin tapauksessa samankokoisia neliömatriiseja. Laskutoimitukset ovat silloin normaaleja, keskimmäisen sarakkeen pisteettömiä operaattorisymboleja, emmekä niitä siksi tässä yleisesittelyssä ryhdy esimerkein valaisemaan.
| Matlab | Maple |
|---|---|
| >> muuttuja=lauseke Loppumerkki ei pakollinen (;) estää tulostuksen |
> muuttuja:=lauseke;
Loppumerkki (; tai :) pakollinen, kaksoispiste estää tulostuksen. |
Muuttujan nimissä erotellaan pienet ja isot kirjaimet, siten esimerkiksi x ja X edustavat eri muuttujaa. Tämä pätee niin Maplen kuin Matlabin suhteen. Tuttu englanninkielinen termi "case sensitive" pätee siten molempiin.
Kuten todettu, Matlabissa ei ole vapaita muuttujia, kuten Maplessa. Tämä yksinkertaistaa evaluointimekanismia merkittävästi. Jos evaluonnissa törmätään muuttujaan, jolla ei ole arvoa, saadaan virheilmoitus. (Maplen evaluointisääntöjä on käsitelty mm. viitteessä [HAM].)
Matemaattisten lausekkeiden käsittely on siten Maplessa mukavampaa ja luontevampaa (myös vapaiden muuttujien takia).
Toisaalta Maplessa on tiettyjä komplikaatioita matriisien käsittelyssä. Asia
on paranemaan päin versiossa Maple 6 kehitetyn LinearAlgebra- pakkauksen
ansiosta. Kuitenkin siirtymäkauden hankaluuksia esiintyy, koska nykyisellään on
myös tarvetta vanhempaan linalg-syntaksiin.
Matlab on numeeristen
matriisien käsittelyssä ylivertaisen yksinkertainen ja lisäksi tehokas Mapleen
verrattuna. (Symbolisia matriiseja ei Matlabilla tietenkään voi käsitellä.)
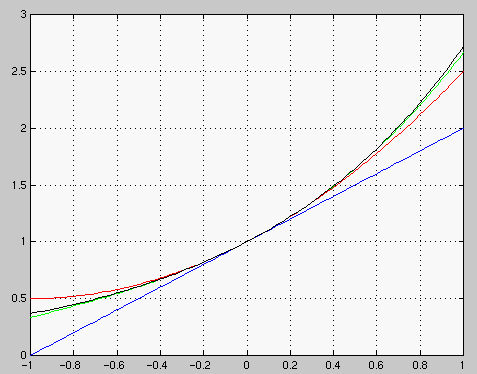
Esimerkki "algebrallisesta" lausekkeesta
x=linspace(-1,1); y1=1+x; y2=y1+(x.^2)/2; y3=y2+(x.^3)/(1*2*3); plot(x,y1,'b',x,y2,'r',x,y3,'g',x,exp(x),'k') shg grid |

Tehtävä Suorita Matlabissa yllä olevat komennot. Piirrä samaan kuvaan vielä astetta 5 oleva Taylorin polynomi jollain edellisistä erottuvalla värillä. Voit joko editoida komentoikkunassa yllä olevaa plot-komentoa tai lisätä yksittäisen kuvaajan komentamalla ennen piirtämistä hold on .
Esimerkki matriisilausekkeesta
>> rand('state',0)
>> A=rand(2,2);
>> S1=eye(2,2)+A;
>> S2=S1+(A^2)/2;
>> S3=S2+(A^3)/(1*2*3);
>> S4=S3+(A^4)/(1*2*3*4);
>> [A,S1,S2,S3,S4,expm(A)]
ans =
Columns 1 through 7
0.9501 0.6068 1.9501 0.6068 2.4716 1.0426 2.6704
0.2311 0.4860 0.2311 1.4860 0.3971 1.6742 0.4642
Columns 8 through 12
1.2187 2.7278 1.2702 2.7441 1.2849
1.7383 0.4838 1.7562 0.4894 1.7613
|
Tulosta on syytä katsoa ajattelemalla sitä vierekkäisinä 2 x 2-matriiseina. Kirjoitetaan yleisemmin for-silmukalla, käytetään samalla uudempaa Matlabin tietorakennetta, solumatriisia, jossa kukin 2 x 2 - matriisi on alkiona "matriisivektorissa" P. (Solumatriisin käyttö ei olisi mitenkään välttämätöntä, sen hyöty tässä yhteydessä on lyhentää laskentakaavaa jakamalla toiminta kahteen for-silmukkaan. Saammepa samalla ensituntuman uuteen tietorakenteeseen (versiossa 5 tulleeseen).
Laskemme siis summia:
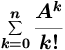
>> for k=1:20; P{k}=(A^k)/prod(1:k); end % Tässä on kätevää käyttää
% solumatriisia P ("cell array")
>> S=eye(2,2);for k=1:20; S=S+P{k}; end
>> [S,expm(A)]
ans =
2.7441 1.2849 2.7441 1.2849
0.4894 1.7613 0.4894 1.7613
>> format long % Täysi tulostustarkkuus
>> [S,expm(A)]
ans =
2.74410134440431 1.28494639715736 2.74410134440431 1.28494639715736
0.48941951062196 1.76130317613298 0.48941951062196 1.76130317613298
>> format short % Palataan alkuperäiseen tulostustarkkuuteen.
|
Lukija, joka tuntee matriisieksponenttifunktion, huomaa heti, että tässä
laskettiin
Sellaiselle lukijalle, joka ei ole tätä käsitettä kohdannut,
esimerkki toimikoon johdatuksena aiheeseen tai sitten vain muodollisena
matriisinmuodostamisesimerkkinä.
Esim:
Viimeinen esimerkki havainnollistaa sitä, että pienenevän jonon saamme
kätevästi ottamalla negatiivisen askelpituuden h.
Usein on tarpeen jakaa annettu väli tasan n:ään osaan.
Se voitaisiin tehdä tyyliin
Funktiolla linspace on myös muoto
Esim:
Mikään ei estä ottamasta mitä tahansa jonoa vektorin indekseiksi kelpaavia
kokonaislukuja (siis välillä 1 ... length(v)). Samaa lukua saa
toistaa ja indeksilukujen järjestys saa hypähdellä miten vain.
Vektorin osalle voidaan sijoittaa arvoksi jokin toinen vektori yksinkertaisesti
tyyliin
Tehtävä: Miten kääntäisit vektorin alkiot vastakkaiseen järjestykseen
kaksoispistettä käyttäen?
Otetaan tässä vertailu Mapleen.
Nämä ja monet muut tuottavat neliömatriisin, jos niitä kutsutaan
vain yhdellä argumentilla. Tämä on joskus epäjohdonmukaista, siksi
suosittelemme aina kahden argumentin käyttöä.
Esimerkki
Esimerkki
Alkuunpääsyosasssa esittelimme lyhyesti
matriisin osiin viittausta.
Kerrataan vielä:
Neuvo: Kun muutat matriisia edellä olevaan tyyliin, kannattaa
varmuuden vuoksi ensin katsoa, että kyseessä on juuri se matriisin osa,
jota todella haluat muuttaa. Niin juuri menettelimme yllä.
Huom Tällaisissa sijoituksissa alkuperäinen matriisi muuttuu.
Siksi kannattaa useissa tapauksissa tallettaa ensin matriisin kopio
toiselle nimelle, jota sitten modifioidaan.
Tyypillinen esimerkki on Gaussin eliminaation rivioperaatiot.
Tehtäviä:
Gaussin eliminointi ...
Vertailuoperaattorit voidaan ajatella funktioiksi, joiden argumentit ovat
operaattorimerkin molemmin puolin, voidaan puhua vasemmasta ja
oikeasta argumentista.
Vertailufunktiot toimivat kohdassa 4.1.1 käsiteltävien skalaalaarifunktioiden
tavoin.
Tämä tarkoittaa:
Huomataan, että totuusarvot ovat myös numeerisia, mutta kääntäen numeeriset
funktiot (kuten zeros, ones) tuottavat numeerisen tuloksen, joka ei ole tyyppiä
"logical".
Edellistä voidaan hyödyntää usein kätevästi suorittamalla laskutoimituksia
totuusarvoilla 0 ja 1, jälkimmäinen on hyvä tiedostaa. Palaamme asiaan
find-komennon yhteydessä kohdassa 2.3.2.
Merkkijonojen ("string") suhteen kannattaa tässä yhteydessä mainita myös
konversiofunktiot num2str ja str2num
Jos haluat hassutella merkkijonoilla, niin kokeilepa hyvin vuoksi, mitä antaa
>> merkki10+0 . Tälle on luonnollinen
(ASCII-) selitys, mutta älä nyt juutu kuitenkaan.
Esimerkki loogisista operaatioista vektoreilla
Esimerkki all- ja any- funktioista matriiseilla
Tällaisia yhdistelmiä voidaan soveltaa luovasti.
Huomaamme (jos olemme lukeneet pitemmälle), että all ja
any
ovat skalaarifunktioita
Esimerkiksi integraalimuunnosten yhteydessä tarvitaan usein paloittain
määritellyn funktion esitystä karakterististen funktioiden (Heavisiden
funktioiden) lineaarikombinaationa.
Matlabissa välin karakteristinen funktio voidaan esittää ällistyttävän
näppärästi ja vähäeleisesti.
Esimerkki
Jos haluaisimme tarkemman kuvan, voisimme ottaa hienomman
diskretoinnin. Tässä tapauksessa olisi toki piirtämisen kannalta ekonomisinta
valita 6 pistettä älykkäästi, kuvaajahan koostuu viidestä jananpätkästä.
Erityisesti, jos H on Heavsiden funktio (ts. positiivisen
reaaliakselin karakteristinen funktio), niin siirretty funktio H(x-a)
saadaan Matlab-lausekkeella >> x > a .
Huomaamme, kuinka kätevää on, että totuusarvoilla 0 ja 1 voi suorittaa myös
tavallisia aritmeettisia laskutoimituksia.
Harjoitustehtäviä paloittain määritellyistä funktioista.
Ota Vastaavia Maple-tehtäviä K/P3-matskuista, Laplace-muunnosten yht.
Muista myös Cooper (tekijälle muistutus!)
Esimerkki
Usein on tarvetta valita vektorista alkiot, jotka toteuttavat tietyt ehdot.
Voimme esimerkiksi tarvita kaikki alkiot, jotka ylittävät jonkin kynnysarvon.
(Pankinjohtaja voi haluta valita avainasiakkaikseen kaikki ne, joiden
pankkitalletusten vuoden keskiarvo ylittää 20 000 euroa. Tästä harjoitustehtävä!)
Funktio find palauttaa nollasta poikkeavien vektorin alkioiden
indeksit. Ehtovektoreitahan osaamme muodostaa loogisilla ja
järjestysoperaatioilla.
Esimerkki
Yleensä kirjoitetaan suoraan Matlab sallii myös find-funktion poisjättämisen yllä: Indeksointiin voidaan ajatella lisättäväksi sellainen sääntö, että
indeksointi
loogisella vektorilla toimii niin, että valitaan ykkösiä vastaavat
vektorin
alkiot ja jätetään nollia vastaavat valitsematta.
Varjopuolena on, että looginen
ja numeerinen (0/1)-vektori (sanomme lyhyesti: "bittivektori") näyttää
samalta,
mutta edellinen toimii, kun taas jälkimmäinen johtaa virheeseen.
Suositus (jota emme kuitenkaan aina itse noudata): Käytä find-funktiota ehtovalintatilanteissa.
Tehtävä Valitse annetusta vektorista parittomia (vastaavasti
parillisia) indeksejä vastaavat alkiot.
Ratkaisu
Eleganttia on käyttää jakojäännosfunktiota rem
Funktio find on valmiiksi ohjelmoitu niin, että kutsu
Toisaalta funktiota voidaan myös kutsua : Esimerkki
Olkoon A vaikkapa edellinen 4 x 4-taikaneliö (tai mikä tahansa matriisi).
Kirjoita Matlab-lauseke, joka korvaa 0:lla kaikki ne A:n luvut, jotka eivät ole
jaollisia 3:lla.
Ratkaisu
Toisaalta ohjausrakenteiden välttelyssä ei kannata mennä liiallisuuksiin.
Pääperiaatteena voidaan pitää sitä, että vektorin komponentteja tai matriisin
alkioita ei tule yleensä pyörittää for-silmukoissa. Sitä voidaan pitää
moukkamaisen Matlab-tuhertajan amatöörimäisenä puuhana.
Sensijaan käsiteltäessä pienehköä lukumäärää pitkiä vektoreita tai matriiseja,
voidaan hyvin sallia niiden suhteen suoritettava silmukointi. Tällöin ei
vielä ole isompaa kasvojen menetyksen riskiä.
Toki on laskentatehtäviä, jotka eivät "vektoroidu". Jos vektorin seuraava
komponentti riippuu edellisistä, on kyseessä iteratiivinen prosessi.
Tällöin on pakko turvautua ohjelmasilmukkaan. Kannattaa toki miettiä,
voiko iteraation toteuttaa siten, että samantien iteroidaan kokonaisilla
vektoreilla.
Ota oma fraktaaliesimerkki
Tyypillisimmin lauseke on skalaari.
Yleisesti
Koodi voidaan kirjoittaa samalle riville, silloin rivinvaihdot on korvattava
pilkuilla. Selkeyden takia on syytä suosia yllä olevaa kirjoitustapaa
sisennyksineen. Esimerkki
Kirjoitetaan koodi, joka palauttaa arvon 0, jos luku on 0, arvon 1, jos se on
positiivinen tai Inf, arvon -1, jos negatiivinen tai -Inf ja virheilmoituksen,
jos "luku" on kompleksinen tai NaN.
Vaikka tällainen rakenne voidaan kirjoittaa suoraan Matlab-istuntoon, se ei
ole mitenkään järkevää. Kirjoitamme koodin tiedostoon ifesim.m .
Laitamme alkuun input-lauseen, joka kysyy käyttäjältä syötelukua n.
Switch-esimerkki
Kirjoitetaan muunnelma edellisestä, joka sopii switch-rakenteelle. Tehdään se
tiedostoon switchesim.m .
Switch-rakenne soveltuu siis tilanteeseen, jossa haaraudutaan muutaman
"vaihdemuuttujan" arvon mukaan. Toisin kuin if-lauseessa, tässä ei käytetä
loogisia ehtoja, vaan rakenne itsessään sisältää "vaihdemuuttujan" vertailun
"tapausarvoon".
Näyttää siltä, että kompleksinen vaihdemuuttuja toimii jonkin tämän
kirjoittajalle vaikeasti aukeavan logiikan mukaisesti. En voi nyt muuta kuin
suositella pitäytymistä reaalisissa (tai käyttämään if-rakennetta).
Yllä oleva koodi toimii järkevästi reaaliluvuilla sekä syötteillä Inf,-Inf,
NaN ja 'kissa'. Kompleksilukujen suhteen se puhuu joskus palturia.
Esimerkki (tyhmä)
Lasketaan vektorin alkioiden itseisarvojen summa "vääräoppisella, tuhertajan tyylillä".
Esimerkki (viisaampi)
Iteroidaan neliöjuurifunktiota annettuun lähtäarvoon ja talletetaan koko
iteraatiojono vektoriksi iterjono .
Jos kirjoitamme yllä merkityn osan tiedostoon iter.m, voimme edetä
Matlab-istunnossamme seuraavaan tapaan:
Esimerkki sisäkkäisistä silmukoista, Hilbertin matriisi
Muodostetaan ns. Hilbertin matriisi, jonka alkiot ovat H(i,j)=1/(i+j-1).
Tässä on esimerkki tilantessa, joka on varmasti helpointa kirjoittaa
alkiotason silmukointina. (Hyväksymme tarpeen tullen poikkeuksia
"tuherrussäännöstä, etenkin jos se koskee meitä itseämme :-). )
Matriisioperaatioratkaisu vaatii hieman kokemusta.
Itse asiassa Matlabissa on valmis funktio hilb, jonka on kirjoittanut
Matlab:n luoja, Cleve Moler. Koodin voi katsoa komennolla type hilb
.
While-rakenne on sopivampi iterointiin kuin for sikäli, että
lopetusehto voidaan ottaa luontevasti mukaan.
Esimerkki, kone-epsilon
Tämä koodi voi antaa "pahimmassa tapauksessa" arvon eps/2 riippuen
alkuarvosta. Kone-epsilonin tapauksessa tärkeää on tietää suuruusluokka,
kertoimella 2 ei ole merkitystä.
eA:n osasumma (n=20) ja verrattiin tulosta
Matlabin oman matriisieksponenttifuntion antamaan tulokseen.
-> Sisällysluetteloon <-
2.2 Vektorin ja matriisin osat ja kokoaminen
2.2.1. Vektorit ja kaksoispiste
Vektorin luominen
Kaksoispistenotaation olemme jo nähneet monessa paikassa.
a:b % vektori: [a,a+1,...,b]
a:h:b % vektori: [a,a+h,...,b]
Viimeinen alkio voi jäädä b:tä vähän pienemmäksi, jos jako "ei mene
tasan", mutta se on harvemmin tärkeää. Kun klikkaat
colon , saat Matlab:n help colon- ohjetekstin.
>> -5:6
ans =
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
>> -3.1:0.1:-2
ans =
Columns 1 through 7
-3.1000 -3.0000 -2.9000 -2.8000 -2.7000 -2.6000 -2.5000
Columns 8 through 12
-2.4000 -2.3000 -2.2000 -2.1000 -2.0000
>> 2:-0.5:-1
ans =
2.0000 1.5000 1.0000 0.5000 0 -0.5000 -1.0000
h=(b-a)/n
x=a:h:b
Tähän on myös valmis funktio linspace,
vanha tuttavamme.
>> x=linspace(a,b,n);
linspace(a,b),
jolloin n:n oletusarvona
käytetään lukua 100.
Tämä on tavallisessa käyrien
piirtämisessä usein sopiva arvo.
Vertailua Mapleen
Maplessa perustyökalu vastaaviin säännöllisiin jonoihin on seq .
Yllä oleva voitaisiin hoitaa Maplessa tähän tyyliin:
> a:=-Pi: b:=Pi: n:=20:
> h:=(b-a)/n;
h := 1/10 Pi
> x:=seq(a+k*h,k=0..n);
x := -Pi, - 9/10 Pi, - 4/5 Pi, - 7/10 Pi, - 3/5 Pi, - 1/2 Pi, - 2/5 Pi,
- 3/10 Pi, - 1/5 Pi, - 1/10 Pi, 0, 1/10 Pi, 1/5 Pi, 3/10 Pi, 2/5 Pi,
1/2 Pi, 3/5 Pi, 7/10 Pi, 4/5 Pi, 9/10 Pi, Pi
-> Sisällysluetteloon <-
Vektorin osat ja modifioiminen
Vektorista v voidaan poimia alkio indeksoimalla tyyliin
v(3). Indeksinä
voidaan käyttää kokonaislukuvektoria, joka usein muodostetaan kaksoispisteen
avulla, tällöin siis viitataan osavektoriin.
>> v=rand(1,7)
v =
0.7382 0.1763 0.4057 0.9355 0.9169 0.4103 0.8936
>> v(2:5)
ans =
0.1763 0.4057 0.9355 0.9169
>> v([1 1 1 2 7 6 6 3])
ans =
Columns 1 through 7
0.7382 0.7382 0.7382 0.1763 0.8936 0.4103 0.4103
Column 8
0.4057
>> v(1:4)=[2 4 6 8]
v =
2.0000 4.0000 6.0000 8.0000 0.9169 0.4103 0.8936
Vastaus
-> Sisällysluetteloon <-
2.2.2 Matriisit ja niiden osat
Matriisien rakentelu osista ja matriisifunktioilla
Opimme edellä perustavat matriisien muodostamiseen, kuten
>> A=[1 2 3;4 6 5]
Matlabissa on koko joukko tehokkaita funktioita erilaisten matriisien
muodostamiseen. Eri tavoin muodostetuista osamatriiseista
voidaan rakentaa isompia matriiseja näitä periaatteita noudattaen:
Esim:
>> A=[1 2 1;-1 2 3;-10 -11 -12]
A =
1 2 1
-1 2 3
-10 -11 -12
>> b=[1;1;1]; % tai b=ones(3,1)
>> Ab=[A,b]
Ab =
1 2 1 1
-1 2 3 1
-10 -11 -12 1
>> A_alle_trb=[A;b']
A_alle_trb =
1 2 1
-1 2 3
-10 -11 -12
1 1 1
>> [A,A,A]
ans =
1 2 1 1 2 1 1 2 1
-1 2 3 -1 2 3 -1 2 3
-10 -11 -12 -10 -11 -12 -10 -11 -12
Matriisienmuodostamisfunktioiden esittelyä
Nollamatriisi, ykkösmatriisi ja yksikkömatriisi saadaan funktioilla
zeros(m,n), ones(m,n), eye(m,n)
("eye" lausutaan samalla tavoin kuin I.)
>> [zeros(2,3),eye(2,2),ones(2,4)]
ans =
0 0 0 1 0 1 1 1 1
0 0 0 0 1 1 1 1 1
>> eye(size([ans;ans]))
ans =
1 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0
Eräitä matriisinmuodostamisfunktioita
ones Ykkösistä koostuva matriisi
zeros Nollamatriisi
rand Satunnaislukumatriisi
diag Vektorista diagonaalimatriisi,
matriisin diagonaalivektori
spdiags Harvan matriisin muodostaminen diagonaaleista.
blkdiag Lohkodiagonaalimatriisi
repmat Matriisin rakentaminen toistamalla lohkoa.
>> A=rand(3,4)
A =
0.4451 0.4186 0.2026 0.0196
0.9318 0.8462 0.6721 0.6813
0.4660 0.5252 0.8381 0.3795
>> diag(A)
ans =
0.4451
0.8462
0.8381
>> diag(diag(A))
ans =
0.4451 0 0
0 0.8462 0
0 0 0.8381
>> repmat(eye(2,2),2,3)
ans =
1 0 1 0 1 0
0 1 0 1 0 1
1 0 1 0 1 0
0 1 0 1 0 1
>> blkdiag(diag([-1,1]),2*ones(2,2))
ans =
-1 0 0 0
0 1 0 0
0 0 2 2
0 0 2 2
>> [diag([-1,1]),zeros(2,2);zeros(2,2),2*ones(2,2)]
Osamatriisit
SKK ss 23 - 25, HIG s. 5
A(:,[2,4,7]) A:n sarakkeet 2,4,7 kokonaisuudessaan.
A(2:4,[2,4,7]) Samoista sarakkeista rivit 2,3,4.
A(:) A:n kaikki alkiot jonoutettuina sarakkeittain.
Aivan kuten vektorien tapauksessa, voidaan matriisin osaa muuttaa
suoralla sijoituksella vastaavaan osamatriisiin tähän tapaan:
» A=reshape(1:15,3,5)
A =
1 4 7 10 13
2 5 8 11 14
3 6 9 12 15
» A(1:2,[1 3 5])
ans =
1 7 13
2 8 14
» A(1:2,[1 3 5])=-ceil(10*rand(2,3))
A =
-10 4 -2 10 -10
-8 5 -5 11 -10
3 6 9 12 15
» A(1:2,[1 3 5])=-1
A =
-1 4 -1 10 -1
-1 5 -1 11 -1
3 6 9 12 15
A(1:2,[1 3 5])=-ones(2,3) % Edellinen muoto tuottaa saman, kts. alla.
Kaksi viimeistä komentoa havainnollistavat sitä, että jos korvaavan matriisin
alkiot ovat samoja, riittää antaa tuo yhteinen skalaari sijoituslauseessa.
(Tämä on tavallaan "skalaarin laajennussäännön ilmentymä".)
2.2.3 Taulukointia
Etsi jostakin!!!
Laajempia esimerkkejä
Kunhan ehditään ...
-> Sisällysluetteloon <-
2.3 Datan käsittelyä, ehdollista valintaa
2.3.1 Relaatiot ja loogiset operaatiot
Vertailuoperaattorit
yhtäsuuri
erisuuri
pienempi
suurempi
pienempi tai yhtäsuuri
suurempi tai yhtäsuuri
==
~=
<
>
<=
>=
Esimerkkejä
Skalaarin ja skalaarin vertailu >> 2==3, 2<3
ans =
0
ans =
1
Matriisin ja matriisin vertailu >> A=[0 1;2 1],B=ones(size(A)),C=zeros(size(A)),E=eye(2,2)
A =
0 1
2 1
B =
1 1
1 1
C =
0 0
0 0
E =
1 0
0 1
>> A==B
ans =
0 1
0 1
>> A<=C
ans =
1 0
0 0
>> A>E
ans =
0 1
1 0
>> E==(E ~=0)
ans =
1 1
1 1
>> E=(E ~=0) % Pieni kompa: Suoritetaan sijoitus muuttujaan E.
E = % Se ei tässä tapauksessa muuta mitään.
1 0
0 1
Skalaarin ja matriisin vertailu >> A=rand(10,10);
>> A>=0.5
ans =
1 0 0 0 1 0 1 0 0 0
0 0 0 1 0 0 0 0 0 0
1 1 1 0 1 0 0 0 1 0
0 1 0 1 1 0 0 0 1 0
0 0 1 1 0 0 1 0 0 1
0 1 1 0 0 0 0 1 0 0
1 1 1 1 1 1 0 1 1 1
1 0 1 0 1 0 1 1 0 0
1 1 0 0 0 0 1 0 1 0
1 0 0 1 1 1 1 1 1 1
Tämä on kätevä tapa selvittää niiden alkioiden paikat, jotka toteuttavat
annetun ehdon (tässä tapauksessa ehtona on " olla >= 0.5 " ).
Loogisia funktioita: is*
Valikoima is*-funktioita (helppilinkkeineen)
ischar
isempty
isequal
isfinite
isieee
isinf
isnan
isnumeric
islogical
isprime
issparse
>> luvut10=1:10
luvut10 =
1 2 3 4 5 6 7 8 9 10
>> tosi10=luvut10==luvut10
tosi10 =
1 1 1 1 1 1 1 1 1 1
>> epatosi10=luvut10 ~=luvut10
epatosi10 =
0 0 0 0 0 0 0 0 0 0
>> ykkoset10=ones(1,10)
ykkoset10 =
1 1 1 1 1 1 1 1 1 1
>> nollat10=zeros(1,10)
nollat10 =
0 0 0 0 0 0 0 0 0 0
>> isnumeric(tosi10)
ans =
1
>> islogical(ykkoset10)
ans =
0
>> tosi10-tosi10
ans =
0 0 0 0 0 0 0 0 0 0
>> isequal(ans,nollat10)
ans =
1
>> 2*tosi10
ans =
2 2 2 2 2 2 2 2 2 2
>> 2*tosi10-3.5
ans =
Columns 1 through 7
-1.5000 -1.5000 -1.5000 -1.5000 -1.5000 -1.5000 -1.5000
Columns 8 through 10
-1.5000 -1.5000 -1.5000
>> luvut10=1:10
luvut10 =
1 2 3 4 5 6 7 8 9 10
>> ischar(luvut10)
ans =
0
>> merkki10=num2str(luvut10)
merkki10 =
1 2 3 4 5 6 7 8 9 10
>> ischar(merkki10)
ans =
1
>> isnumeric(str2num(merkki10))
ans =
1
>> isequal(str2num(merkki10),luvut10)
ans =
1
>> isequal(str2num(merkki10),merkki10)
ans =
0
>> isequal(merkki10,num2str(luvut10))
ans =
1
Loogiset operaattorit
ja (and)
tai (or)
ei (not)
"joko tai"
tosi, jos kaikki alkiot ~= 0
tosi, jos jokin alkio ~= 0
&
|
~
xor
all
any
>> x=[-2,1,0,5];
>> y=[-2,-1,0,1];
>> (x>0) | (y>0)
ans =
0 1 0 1
>> (x>0) & (y>0)
ans =
0 0 0 1
>> A=reshape(1:6,3,2)'
A =
1 2 3
4 5 6
>> B=A; B(2,2)=-B(2,2)
B =
1 2 3
4 -5 6
>> all(A==B) % all-funktiota sovelletaan sarakkeittain,
ans = % identtiset sarakkeet antavat 1:n (ja vain ne).
1 0 1
>> all(all(A==B)) % Näin voidaan testata, ovatko matriisien kaikki
ans = % alkiot samat.
0
>> any(A==B) % any-funktiota sovelletaan sarakkeittain.
ans = % Jos vastinsarakkeissa on jotkin samat
1 1 1 % vastinalkiot, saadaan 1, muuten 0.
>> any(any(A==B)) % Onko edes yksi vastinalkiopari sama?
ans = % Tässä tapauksessa on (monikin).
1
>> all(any(A==B)) % Onko jokaisessa vastinsarakkeessa ainakin yksi
ans = % sama vastinalkiopari?
1
Matemaattinen sovellus - välin karakteristinen funktio
Monessa
yhteydessä on hyödyllistä käsitellä jonkin joukon A karakteristista funktiota
ChiA . Kyseessä on funktio, joka saa joukon A pisteissä arvon
1 ja muualla arvon 0.
Ajatellaan, että x on diskretoitu x-akseli
(tietysti käytännössä äärellinen osa sitä) ja a ja b skalaareja. Matlab-lauseke >> (x > a) & (x < b)
antaa x:n pituisen vektorin, joka käyttäytyy halutulla tavalla.
a=0;b=1;
x=linspace(a,b,20) % Karkea diskretointi havainnollistuksen vuoksi.
y=(x>a) & (x < b)
plot(x,y); % Yhdistetään vektorien x ja y vastinpisteet jananpätkillä.
axis([-1,2,-0.1,1.1]);grid;shg % Parannellaan kuvan ulkoasua.
2.3.2 Datan käsittelyä,
ehdollista valintaa, mieti ots!
find, (sum, max, min)
Muistutamme
aluksi, että vektorista v voidaan poimia alkioita indeksoimalla
kokonaislukuvektorilla, jonka alkiot ovat välillä 1, ..., n , missä n
on vektorin pituus.
>> rand('state',0) % Kokeen toistettavuuden takia alustus.
>> v=floor(10*rand(1,8)) % Satunnaisia kokonaislukuja välillä [0,10].
v =
9 2 6 4 8 7 4 0
>> indvek=[1 1 3 4 2 2 6 1 7 5 5 5]; % indeksivektori saa olla miten
% pitkä tahansa, toistoja saa esiintyä
>> v(indvek)
ans =
9 9 6 4 2 2 7 9 4 8 8 8
>> x=[0,1,-3,5,0];
>> ind=find(x)
ind =
2 3 4
>> x(ind)
ans =
1 -3 5
>> x=[x,2*x,-x] % Rakennetaan pitempi ja luvuiltaan vaihtelevampi vektori
x =
Columns 1 through 12
0 1 -3 5 0 0 2 -6 10 0 0 -1
Columns 13 through 15
3 -5 0
>> ind=find(x>=2)
ind =
4 7 9 13
>> x(ind)
ans =
5 2 10 3
x(find(x>=2)) , mikä on helppo
omaksua idiomina.
x(x>=2)
toimii yhtä hyvin.
Jos ajattelemme tätä idiomina, se on sinänsä
luonteva (ja pankinjohtajankin helposti omaksuttavissa).
Sensijaan indeksoinnin
kannalta ajateltuna siinä on näennäinen ristiriita: edellähän olemme oppineet,
että 0 ei kelpaa indeksiksi.
>> v=... % Jokin vektori
>> indeksit=1:length(v) % v:n indeksivektori
>> v(find(rem(indeksit,2)==0)) % Parillisia vastaavat
>> v(find(rem(indeksit,2)~=0)) % Parittomia vastaavat
Funktio find sovellettuna matriisiin
Funktiota find on helppo soveltaa matriisiin A jonouttamalla A ensin
pitkäksi vektoriksi.
Tämähän saadaan aikaan kirjoittamalla A(:) . Tällöin indeksointi
tapahtuu yhdellä indeksillä ja palautuu näin vektoritilanteeseen.
ind=find(A) tekee tuon jonoutuksen.
(Ei siis tarvitse kirjoittaa: ind=find(A(:)) .)
Kaiken lisäksi matriisit ymmärtävät myös jonoutetun indeksin käytön, ts.
jos matriisille annetaan indeksivektori, se tulkitsee sen luvut jonoutetun
matriisin indekseiksi.
[i,j]=find(A)
Tällöin
palautetaan indeksivektorit i ja j,
jotka rinnakkain asetettuna
antavat 0:sta poikkeavien A:n alkioiden paikat. Tämä muoto on erityisen
hyödyllinen käsiteltäessä matriiseja
"harvoina"
("sparse").
A=magic(4) % Olkoon A 4 x 4- "taikaneliö"
ehtomat=mod(A,3)==0 % Mitkä alkiot ovat jaollisia 3:lla ?
ind=find(ehtomat) % Indeksit ovat vektoriksi jonoutetun A:n indeksejä.
% (siis sama kuin find(ans(:))
A(ind) %
A(ind)=33 % Sijoitetaan kuhunkin arvo 33.
A=magic(4) % tms.
A(find(mod(A,3)~=0))=0
2.3.3. Summia ja tuloja,
Jatkoksi
sum, prod
2.3.4. Ohjausrakenteita: for,while,
if, switch
Matlabissa on otsikossa mainitut 4 ohjausrakennetta. Pääperiaate on, että
koodi tulisi pyrkiä rakentamaan tehokkaita vektorioperaatioita käyttäen ja
vain
"viime hädässä" tulisi turvautua ohjausrakenteisiin. Silloin koodista tulee
tehokasta ja myös selkeää.
if- ja switch-rakenteet
Yksinkertaisin muoto: if lauseke
komentoja
end
Tässä lauseke on skalaari tai yleisemmin matriisi, joka
tyypillisesti saadaan järjestys- tai loogisilla operaatioilla. Komennot
suoritetaan, jos lausekematriisin kaikki alkiot (tarkemmin niiden reaaliosat)
ovat nollasta poikkevia.
if-lauseessa voi olla elseif ja else-
haaroja. (elseif on kirjoitettava yhteen.)
Luonnollisesti ohjausrakenteet kirjoitetaan yleensä
m-tiedostoon, vain aivan yksinkertaisissa tapauksissa kannattaa kirjoittaa
suoraan komentoikkunaan.
n=input('Anna luku tai +-Inf ')
' Jos annoit kompleksiluvun tai NaN:n, syytä itseäsi. '
if imag(n)~=0
error('Haluan reaaliluvun')
elseif n < 0
tulos=-1
elseif n==0
tulos=0
elseif n > 0
tulos=1
else
error('Haluan reaaliluvun, tai +/- Inf:n, NaN ei käy. ')
end
n=input('Anna reaaliluku tai +-Inf ')
switch n
case 0
'Annoit luvun 0'
case 1
'Annoit luvun 1'
case -1
'Annoit luvun -1'
otherwise
['Annoit jotain muuta, tarkemmin sanottuna ',num2str(n),':n']
end
for-lause
for muuttuja=vektorilauseke
komennot
end
Muuttuja käy läpi kaikki vektorilausekkeen komponentit ja suorittaa
kullakin komennot. Useimmiten vektorilauske on muotoa 1:n tai
alku:askel:loppu. Mikään ei estä käyttämästä vaikkapa vektoria
[-100, 55, 2+3*i,primes(30),inf]
v=... % Annetaan vektori v
n=length(v);
summa=0;
for k=1:n
summa=summa+abs(v(k));
end;
a=5 % Annetaan iteraation lähtäarvo, olkoon 5
n=10 % Iteraatiokierrosten lukumäärä
%%%%%%%%%%% iter.m alkaa %%%%%%%%%%%%%%%%%%
iterjono=[]; % Alustetaan iterjono tyhjäksi vektoriksi.
uusiarvo=a;
for k=1:n
iterjono=[iterjono,uusiarvo];
uusiarvo=sqrt(uusiarvo);
end;
iterjono
%%%%%%%%%%%%%% iter.m loppuu %%%%%%%%%%%%
a=5;n=10;
iter % Suoritetaan tiedostossa iter.m olevat komennot.
a=iterjono(end) % Uudeksi alkuarvoksi viimeinen edellä saatu arvo
a =
1.0031
>> iter % Suoritetaan tiedostossa iter.m olevat komennot,
iterjono = % alkuarvona on edellisen iteroinnin viimeinen arvo.
Columns 1 through 7
1.0031 1.0016 1.0008 1.0004 1.0002 1.0001 1.0000
Columns 8 through 10
1.0000 1.0000 1.0000
>> format long % Täysi tulostustarkkuus
>> iter % Nyt ei muuteta alkuarvoa, katsotaan edellistä tarkemmin
iterjono =
Columns 1 through 4
1.00314837919044 1.00157295250543 1.00078616722326 1.00039300638462
Columns 5 through 8
1.00019648388935 1.00009823711941 1.00004911735345 1.00002455837517
Columns 9 through 10
1.00001227911220 1.00000613953725
>> format short % Palataan oletustulostustarkkuuteen.
m=4;n=4 % Annetaan m ja n
for i=1:m
for j=1:n
H(i,j)=1/(i+j-1);
end
end
H % Näytä tulos.
H =
1.0000 0.5000 0.3333 0.2500
0.5000 0.3333 0.2500 0.2000
0.3333 0.2500 0.2000 0.1667
0.2500 0.2000 0.1667 0.1429
while-lause
While-silmukan yleinen muoto on while lauseke
komennot
end
Komennot suoritetaan niin kauan kuin lauseke on tosi.
e=1; % Alustus
while 1+e > 1
e=e/2;
end
e
eps % Systeemimuuttuja eps antaa arvion kone-epsilonille
abs(e-eps) % Paljonko eroavat
-> Sisällysluetteloon <-
-> Sisällysluetteloon <-
-> Sisällysluetteloon <-