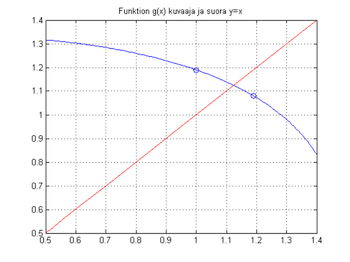
Esimerkki nuolinäppäiniteraatiosta

Määritä funktion

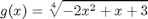
$$\ \ \ \ \ g(x)=\root 4 \of {-2 x^2 + x +3}$$

jokin kiintopiste, ts. piste x, jossa g(x)=x .

Contents

Määritellään funktio g ja piirretään

Käytetään ns. funktio-osoitintyylillä, josta tuonnempana.

g=@(x)(-2*x.^2+x+3).^(1/4)
% Vektoriaritmetiikassa on oltava (.^) .
close all  % Suljetaan vanhat grafiikkaikkunat.
fplot(g,[0.5,1.4]) % Piirretään g välillä [0.5, 1.4]]
hold on
fplot(@(x)x,[0.5 1.4],'r')  % Suora y=x, r - 'red'
grid on
title('Funktion g(x) kuvaaja ja suora y=x')
shg    % show graphics - tuo grafiikkaikkuna esiin.

g = 
    @(x)(-2*x.^2+x+3).^(1/4)

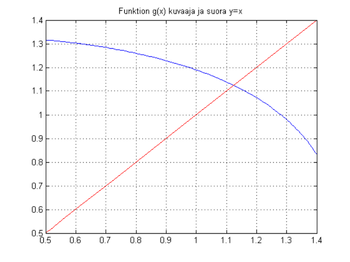
Kiintopisteiteraatio:

Valitaan kuvan perusteella alkupisteeksi x=1. (Otetaan näin kaukaa, että prosessi ei heti lopu.) Koko suoritus on kätevää suorittaa komentoikkunassa tähän tapaan:

x=1;
plot(x,g(x),'o'),x=g(x)
%
% Jälkimmäistä riviä toistetaan nuoli-ylös-ENTER-yhdistelmällä,
% nähdään x:n lukuarvot ja
% kuvassa pisteen (x,g(x)) (hitaahko) kulkeutuminen kohti kiintopistettä.

x =
    1.1892

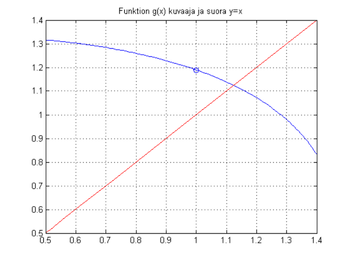
Teepä tämä ja kenties sen innoittaman muitakin kokeiluja.

Helpoimmalla pääset maalaamalla harmaat laatikot ja F9.

(Jos et käytä Matlabin selainta, F9 ei toimi, cut/paste toimii aina)

Sitten jatkat komentoikkunassa iterointia nuolinäppäintä käyttäen napsutellen (Nuoli ylös, ENTER) riviä :

 plot(x,g(x),'o'),x=g(x)

x =
    1.0801


Published with MATLAB® 7.11