Kanttiaallon approksimointia Fourier-sinisarjan osasummilla

The Fourier series expansion for a square-wave is made up of a sum of odd harmonics, as shown here using MATLAB®.

Sisällys

Add an Odd Harmonic and Plot It 

t = 0:.1:pi*4;
y = sin(t);
plot(t,y);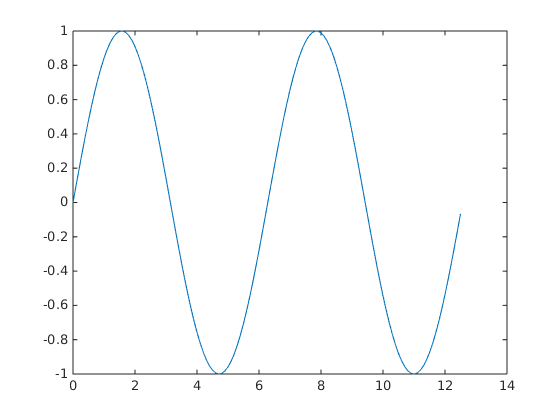

In each iteration of the for loop add an odd harmonic to y. As k increases, the output approximates a square wave with increasing accuracy.

for k = 3:2:9

Perform the following mathematical operation at each iteration:

$$ y = y + \frac{\sin kt}{k} $$ aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa

Display every other plot:

    y = y + sin(k*t)/k;
    if mod(k,4)==1
        display(sprintf('When k = %.1f',k));
        display('Then the plot is:');
        cla
        plot(t,y)
    end

When k = 5.0
Then the plot is: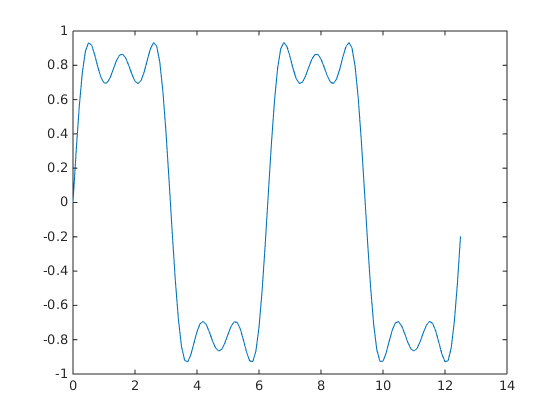

When k = 9.0
Then the plot is: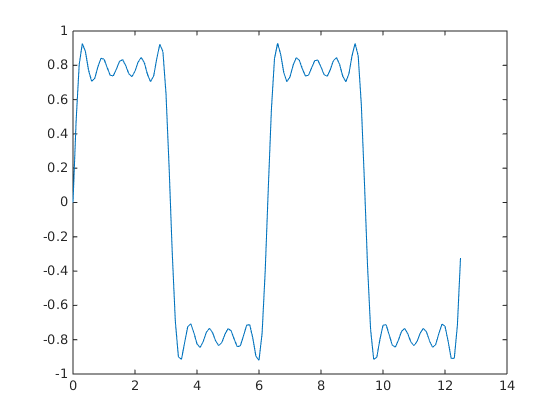

end

Note About Gibbs Phenomenon

Even though the approximations are constantly improving, they will never be exact because of the Gibbs phenomenon, or ringing.


Published with MATLAB® R2014b