Various views of meshgrid
HA 19.10.2016
meshgrid is especially useful for 3d-graphics. Also in any computation where function defined on a 2d-mesh is required.
An easy illustration is to look at multiplication table.
Contents
First attempt: for-loop
clear
close all
x=1:5
x =
1 2 3 4 5
y=1:4
y =
1 2 3 4
for i=1:5 for j=1:4 z(i,j)=i*j; end end z z'
z =
1 2 3 4
2 4 6 8
3 6 9 12
4 8 12 16
5 10 15 20
ans =
1 2 3 4 5
2 4 6 8 10
3 6 9 12 15
4 8 12 16 20
Thus we get the multiplication table in the form Matlab's graphics functions like mesh,surf,contour require. However, it is clumsy and ineffcient.
Using meshgrid
[X,Y]=meshgrid(x,y); % % Put X and Y side by side.
[X Y]
ans =
1 2 3 4 5 1 1 1 1 1
1 2 3 4 5 2 2 2 2 2
1 2 3 4 5 3 3 3 3 3
1 2 3 4 5 4 4 4 4 4
Z=X.*Y % Multiplication table
Z =
1 2 3 4 5
2 4 6 8 10
3 6 9 12 15
4 8 12 16 20
mesh(x,y,Z) xlabel('x-axis') ylabel('y-axis')
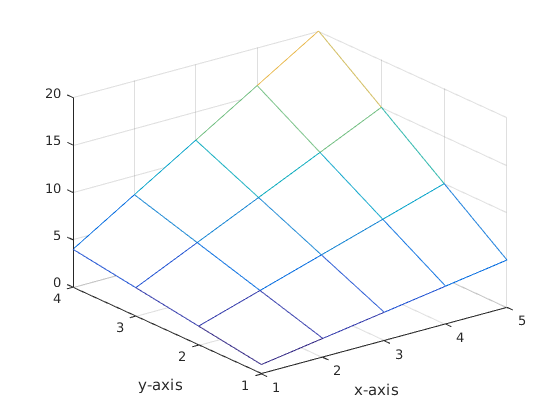
Handy ways to plot gridlines and gridpoints
Look at X and Y side by side again:
[X Y] subplot(1,2,1) imagesc(X) title('X') subplot(1,2,2) imagesc(Y) title('Y') shg
ans =
1 2 3 4 5 1 1 1 1 1
1 2 3 4 5 2 2 2 2 2
1 2 3 4 5 3 3 3 3 3
1 2 3 4 5 4 4 4 4 4
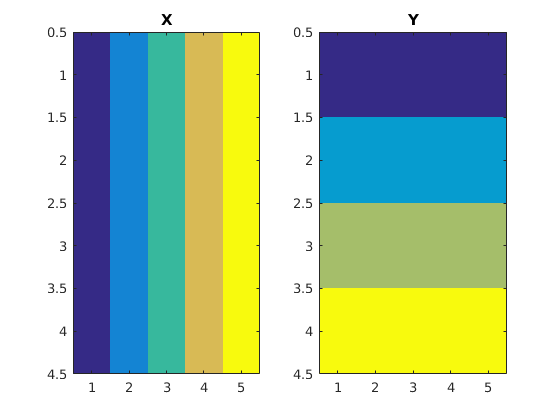
figure % New graphics window plot(X,Y,'k') % Matlab operates rowwise.
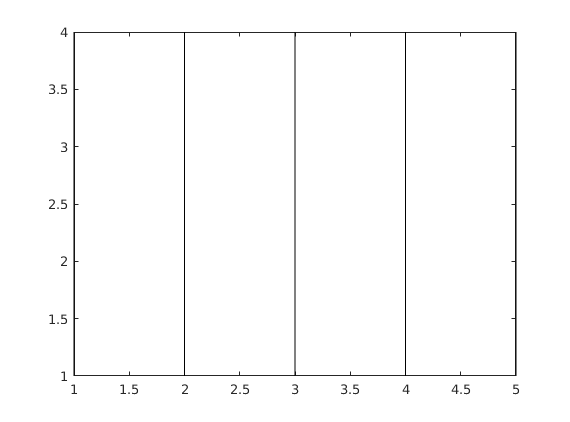
If plot(X,Y) has matrix argumens X,Y of the same size it plots rowwise: plot(X(i,:),Y(i,:)), i=1..m or columnwise plot(X(:,j),Y(:,j)), j=1..n This is a less documented feature. In this case Matlab seems to choose the way that is reasonable looking at the data (sounds a bit incredible). Anyway, it works here, a little confusing, though. Anyway, this procedure is very handy, when you know it.
hold on
[X' Y']
ans =
1 1 1 1 1 2 3 4
2 2 2 2 1 2 3 4
3 3 3 3 1 2 3 4
4 4 4 4 1 2 3 4
5 5 5 5 1 2 3 4
plot(X',Y','k') % Matlab operates columnwise % (Matlab is 'wise')
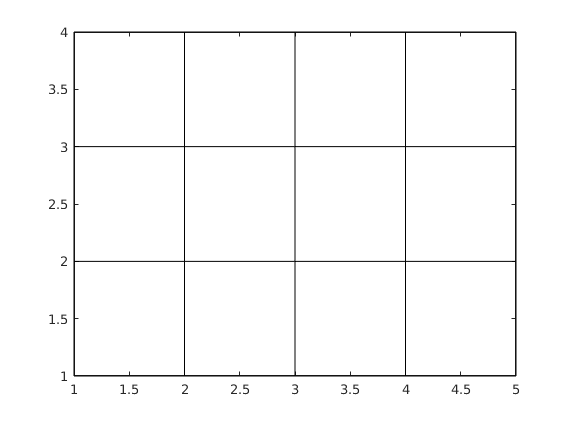
Look at X and Y as long column vectors side by side
[X(:) Y(:)]
ans =
1 1
1 2
1 3
1 4
2 1
2 2
2 3
2 4
3 1
3 2
3 3
3 4
4 1
4 2
4 3
4 4
5 1
5 2
5 3
5 4
plot(X(:),Y(:),'o')
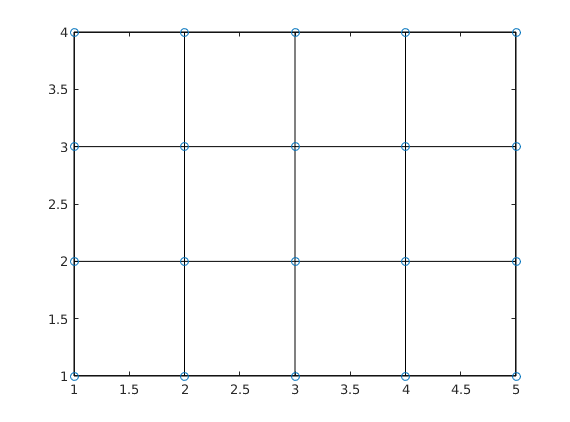
The gridlines can also be seen most easily in 3d by
mesh(x,y,0*Z) % You can look directly from above just rotating the figure % with your mouse. %
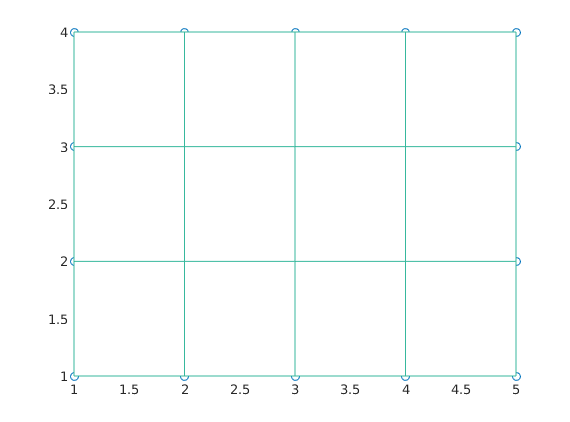
Add grid poins on the surface (plot3), stem3
close all plot3(X(:),Y(:),Z(:),'*') hold on mesh(x,y,Z) grid on stem3(X,Y,Z)
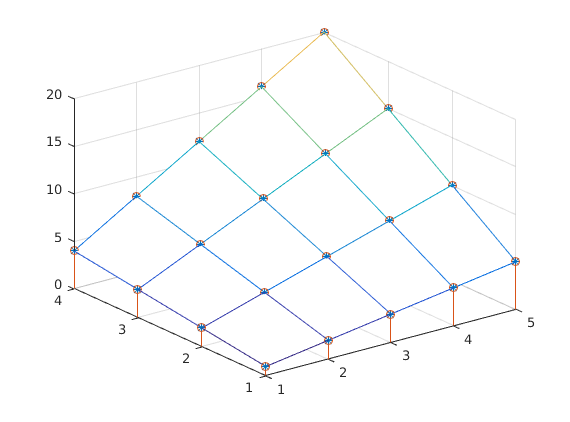
Isn't it nice, all is crystal clear!
Example of surface plot
Above we considered the function f(x,y)=x y. Instead we could have any function of 2 variables f(x,y) Let's take for instance
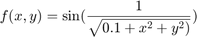
figure x=linspace(-2*pi,2*pi,30); y=x; [X,Y]=meshgrid(x,y); Z=sin(1./sqrt(.1+X.^2+Y.^2)); mesh(x,y,Z)
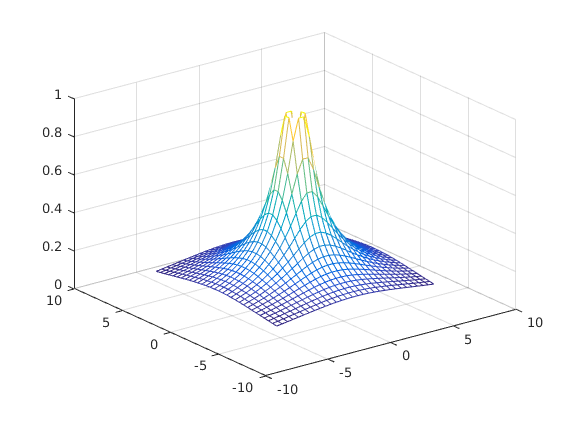
figure surfc(x,y,Z),colorbar xlabel('x-axis') ylabel('y-axis')
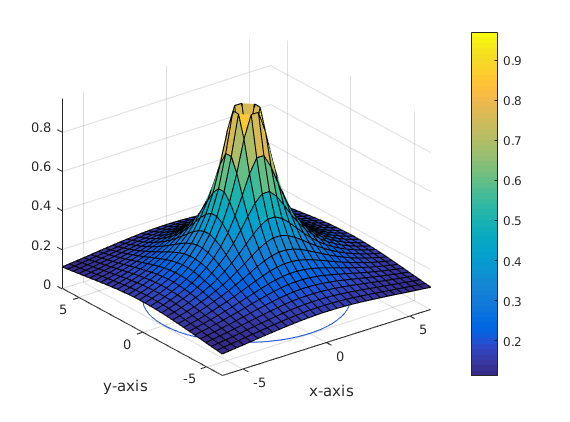
contour(x,y,Z,20)
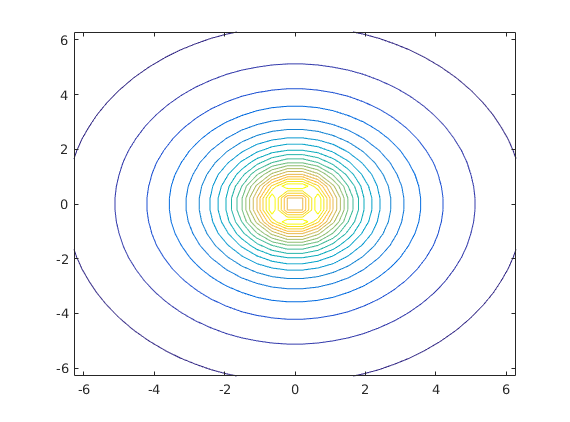
Another example:
f = @(x,y) exp(cos(sqrt(x.^2 + y.^2))); % a function of two variables d = -2*pi:0.1:2*pi; % domain for both x,y [X,Y] = meshgrid(d,d); % create a grid of points Z = f(X,Y); % evaluate f at every point on grid surf(X,Y,Z); shading interp; % interpolate between the points material dull; % alter the reflectance camlight(90,0); % add some light - see doc camlight alpha(0.8); % make slightly transparent box on; % same as set(gca,'box','on')
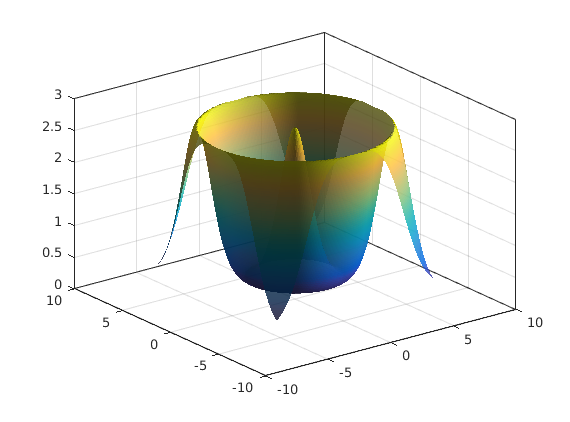
Some nice additions, do later
These were demonstrated already:
%plot3(X(:),Y(:),Z(:),'*') %hold on %surf(x,y,Z) %grid on %
Here is a "raw" session from history with erroneous commands also, pick the "diamonds".
%{ [X(:) Y(:)] plot(X(:),Y(:)) hold on plot(X(:),Y(:),'0') plot(X(:),Y(:),'o') shg hold off plot(X(:),Y(:),'o') shg Z=X(:).*Y(:); surf(x,y,Z) Z=reshape(Z,size(X)); surf(x,y,Z) shg imagesc(X) shg imagesc(Y) shg colorbar shg plot(Z) shg plot(Z,'.') shg [{X},{Y}] cellplot(ans) shg XYcell=[{X},{Y}] celldisp(XYcell) X Y XYcell XYcell{1:2} plot3(X(:),Y(:),Z(:),'*') shg grid3d grid shg hold on mesh(x,y,Z) shg surf(x,y,Z) shg %}