Kelluva sylinteri

Tehtävä. Miten syvällä kelluu alumiiniputki, jonka säde ja vaipan paksuus ? Alumiinin tiheys .

Piirrämme kuvan, jossa näkyy putki ja vedenpinta

> restart:

Piirretään ensin sylinteri. Tähän voidaan käyttää plots -pakkauksen plot3d -funkitota, jolla saadaan yleinen parametrimuotoinen pinta piirretyksi. (Tämä menee hieman yli koulukurssin, mutta nyt on pääasia, että saadaan kuva tavalla tai toisella aikaan.)

> with(plots):

> x:=t;y:=cos(theta);z:=sin(theta);

> X:=t:Y:=1.2*cos(theta);Z:=1.2*sin(theta);

Muodostamme 1-säteisen sylinterin [x,y,z] ja 1.2-säteisen [X,Y,Z], joiden akselina on x-akseli. Jos kiinnitetään t, saadaan ympyrä tasossa x=t, sylinteripinta muodostuu, kun annetaan t:n vaihdella. Piirrämme eri mitoilla, liioiqttelemme havainnollisuuden vuoksi putken paksuutta.

> sisasylinteri:=plot3d([x,y,z],t=-2..2,theta=0..2*Pi,axes=none,grid=[2,50],scaling=constrained,orientation=[20,60],style=patchnogrid,shading=zgreyscale):

> ulkosylinteri:=plot3d([X,Y,Z],t=-2..2,theta=0..2*Pi,axes=none,grid=[2,50],scaling=constrained,style=patchnogrid,shading=zgreyscale):

> vesi:=plot3d(1/3,xx=-4..2,yy=-2.5..2.5,shading=zgreyscale):

> display({sisasylinteri,ulkosylinteri,vesi});

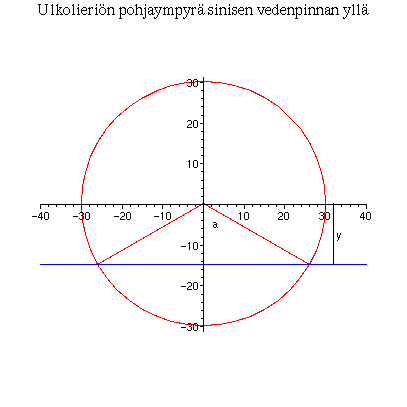
Kuva pohjaympyrästä ja vedenalaisen segmentin alan laskennasta

> x:='x':y:='y':z:='z':

Käytämme ainakin y:tä vapaana symbolina, joten se täytyy vapauttaa edellisestä arvostaan.

Nosteen laskemiseksi tarvitsemme vedenalaisen lieriösegmentin tilavuuden, jota varten laskemme ulkolieriön pohjasegmentin pinta-alan. Piirretään pohjaympyrä ja vedenpinta.

> restart:with(plots):

> R:=30:x:=R*cos(theta);y:=R*sin(theta):
ympyra:=plot([x,y,theta=0..2*Pi]):
t1:=-Pi/6;t2:=Pi+Pi/6;
x1:=R*cos(t1);y1:=R*sin(t1);
x2:=R*cos(t2);y2:=R*sin(t2);
kolmio:=plot([[0,0],[x1,y1],[x2,y2],[0,0]]):
vesi:=plot(y1,xaks=-40..40,color=blue):
mittaviiva:=plot([[32,y1],[32,0]],color=black):
y:='y':yteksti:=textplot([33.5,-7.5,"y"]):
alteksti:=textplot([3,-5,"a"]):
display({kolmio,ympyra,vesi,mittaviiva,yteksti,alteksti},scaling=constrained,title="Ulkolieriön pohjaympyrä sinisen vedenpinnan yllä",labels=["",""]);

>

Ratkaisu

Olemme käyttäneet monia muuttujia, nyt on syytä aloittaa puhtaalta pöydältä.

> restart:

> kolmion_ala:=y*sqrt(R^2-y^2);

Huom! Tässä muodostettiin merkillä varustettu ala.

> sektorin_ala:=(2*alpha)/(2*Pi)*Pi*R^2;

> segmentin_ala:=sektorin_ala-kolmion_ala;

> noste:=g*segmentin_ala*syl_pituus;

> putken_tilavuus:=(Pi*R^2-Pi*(R-d)^2)*syl_pituus;

> putken_paino:=simplify(rho*g*putken_tilavuus);

Muodostamme taspainoehtoyhtälön.

> ehto:=noste=putken_paino;

Maple ei suorita puolittain jakamista, ennekuin vaadimme sitä:

> ehto:=ehto/(g*syl_pituus);

Yhtälön sieventäminen käy parhaiten muodostamalla vasemman puolen ( lhs - left hand side) ja oikean puolen ( rhs - right hand side) erotus.

> ehto:=simplify(rhs(ehto)-lhs(ehto))=0;

> alpha:=arccos(y/R);

Tarkistetaanpa, miten Maple ymmärtää arccos-funktion päähaaran. Kuva näyttää, että se sopii juuri tarkoituksemme.

> plot(arccos(x),x=-1..1);

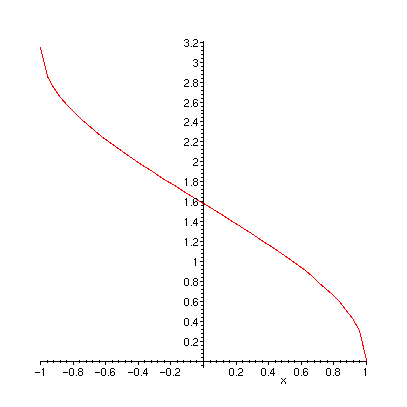
> ehto;

Tässä vaiheessa otamme numeroarvot mukaan. Muistamme, että kun lausekkeessa esiintyville muuttujille annetaan arvoja, ne sijoittuvat automaattisesti lausekkeeseen.

> R:=30;d:=1;rho:=2.7;

> ehto;

Edelleenkin näyttää jokseenkin kaamealta yhtälöltä. Vaan onpa meillä välineet sen selvittelyyn. Katsotaan ensin, miltä yhtälön vasemman puolen kuvaaja näyttää, jotta saamme käsityksen ratkaisujen olemassaolosta, lukumäärästä ja sijainnista.

> F:=lhs(ehto);

> plot(F,y=0..30);

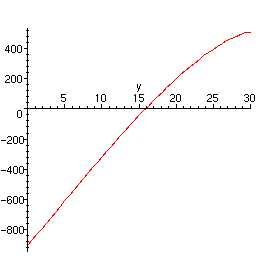
Annamme kuvasta katsomamme karkean likiarvon y=15 numeerisen ratkaisijan lähtöpisteeksi.

> yarvo:=fsolve(ehto,y=15);

> syvyys:=R-yarvo;

Lopullinen kuva

Piirrämme lopuksi putken ja vedenpinnan oikeilla arvoilla.

> X:=t;Y:=R*cos(theta);Z:=R*sin(theta);x:=t;y:=(R-d)*cos(theta);z:=(R-d)*sin(theta);

> sisasylinteri:=plot3d([x,y,z],t=-40..40,theta=0..2*Pi,axes=none,grid=[2,50],scaling=constrained,orientation=[20,60],style=patchnogrid,shading=zgreyscale,axes=boxed):ulkosylinteri:=plot3d([X,Y,Z],t=-40..40,theta=0..2*Pi,axes=boxed,grid=[2,50],scaling=constrained,style=patchnogrid,shading=zgreyscale):
vesi:=plot3d(-yarvo,xakseli=-40..40,yakseli=-30..30,shading=zgreyscale,axes=boxed):
display({sisasylinteri,ulkosylinteri,vesi});

Huomaamme, että oikeilla mitoilla varustettuna sylinteri näyttää hyvin ohuelta, niinpä ei olekaan ihme, että se kelluu näin ylhäällä.