Kaksi pinta-alaesimerkkiä

Solmu-kirjoituksen ideointivaiheessa tehtyjä

HA kesä 1999

Tehtävä 1

Tehtävä: Laske sen alueen pinta-ala, jota rajoittavat y-akseli sekä käyrät , , missä ja ulotettuna niiden ensimmäiseen positiiviseen leikkauspisteeseen saakka.

> f:=x->x*sin(x)*exp(-x);g:=x->cos(x);

> plot([f(x),g(x)],x=0..5);

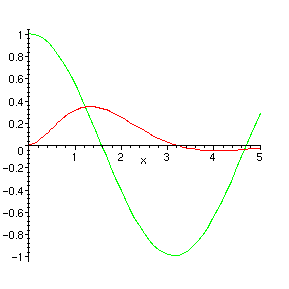
Lasketaan leikkauspiste:

Kuvasta nähdään, että ensimmäinen positiivinen leikkauspiste on varmasti välillä [1,2]. On selvää, että tässä tapauksessa ratkaisua täytyy etsiä numeerisesti. Tähän tarkoitukseen on Maplessa komento fsolve . etukirjain f viittaa sanaan floating point , eli liukuluku . Numeeriselle ratkaisijalle annetaan lähtötiedoksi ensinnäkin ratkaistava yhtälö ja toiseksi väli, jolta ratkaisua etsitään. Sijoitamme samantien ratkaisun muuttujaan b .

> b:=fsolve(f(x)=g(x),x=1..2);

> ala:=int(g(x)-f(x),x=0..b);

Ehkäpä olisi ollut mukava nähdä välivaiheita. No, lasketaan ensin integraalifunktio.

> F:=int(g(x)-f(x),x);

> F:=simplify(F);

Suoritetaan sijoitus integraalifunktioon. Nyt emme määritelleet F:ää Maple-funktioksi, vaan se on pelkästään symbolinen lauseke. Siksi emme voi kirjoittaa sijoitusta muodossa .

Sensijaan on käytettävä Maple-komentoa subs , jolla lausekkeessa esiintyvä muuttuja voidaan korvata halutulla symbolilla (arvolla).

> subs(x=b,F)-subs(x=0,F);

> evalf(%);

Huomaamme, että Maple ei ryhdy laskemaan likiarvoja, ellei sitä erityisesti siihen komenneta liukulukulaskentakomennolla evalf .

Tehtävä 2

Määritä paraabelin pisteeseen (1,1) piirretyn normaalin ja paraabelin rajoittaman alueen pinta-ala.

Tällä kertaa emme määrittele rajaavia käyriä funktioiksi, vaan käsittelemme niitä lausekkeina.

> y:=x^2;dy:=diff(y,x);

Tangentin kaltevuus (kulmakerroin) pisteessä x=1.

> dy1:=subs(x=1,dy);

Normaalin kaltevuus saadaan käänteisluvun vastalukuna.

> nk1:=-1/dy1;

Normaalin yhtälö pisteen (1,1) kautta.

> yn:=1+nk1*(x-1);

Paraabelin ja normaalin leikkauspisteet:

(Yhtälö ilmaistaan muodossa vasen=oikea, solve -komennon ensimmäisenä argumenttina on ratkaistava yhtälö ja toisena tuntematon, tässä x. )

> lpx:=solve(y=yn,x);

Valitsemme integroinnin alarajaksi lpx -jonon ensimmäisen alkion (jonka näemme pienemmäksi) ja ylärajaksi toisen. Jonosta poiminen tapahtuu hakasulkuindeksoinnilla.

> a:=lpx[1];b:=lpx[2];

> plot([y,yn],x=-2..1.5);

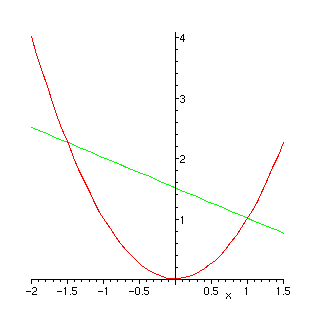
> ala:=int(yn-y,x=a..b);

Suoritamme tässä, kuten edelläkin vielä vaiheittain.

> int(yn-y,x);

Määrittelemme tällä kertaa integraalifunktion oikeaksi Maple-funktioksi. Teknisesti teemme sen tässä maalaamalla edellisen tuloslausekkeen hiirellä ja kopiomalla (leikkaus/liimaus-tyylillä).

> F:=x->3/2*x-1/4*x^2-1/3*x^3;

Nyt emme tarvitse subs -komentoa, vaan voimme kirjoittaa suoraan:

> F(b)-F(a);