Rudinin versio Weierstrassin funktiosta  

Jatkuva funktio, jolla ei ole missään derivaatta. 

17.03.08  Heikki Apiola 

Liittyy Markku Halmetojan kirjoitukseen Solmun numerossa 3/2008. 

                                                                                                 

Maple-ohjelmalla tehtyjä apuvälineitä 

Symbolilaskentaohjelma, kuten Maple, Mathematica tai Maxima on erinomainen apuväline mainitunlaisten funktioiden esittämisessä. Tässä käytetään ensinmainittua. Tarvitsemme operaattoria, joka suorittaa annetun funktion jaksollisen jatkamisen.  

Hieno toteutus on peräisin  Maple-gurulta: Mike Monaganilta 

Jos Maple ei ole tuttu, voit huoletta jättää koodin lukematta (ja vaikka olisikin :-)).

> # Jaksollinen jatko: MapleTech Vol 3 No. 3 1996 (Mike Monagan)
#
JJ:=proc(f,d::range)
 subs({'F'=f,'L'=lhs(d),'D'=rhs(d)-lhs(d)},
 proc(x::algebraic) local y;
   y:=floor((x-L)/D);
   F(x-y*D);
 end)
end:

# Esim:
#sw:=JJ(signum,-1..1);
#plot(sw,-4..4);
#
 

Määritellään Rudinin funktio 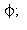phi; 1 

> phi0:=x->abs(x);
 

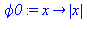
proc (x) options operator, arrow; abs(x) end proc 

>
 

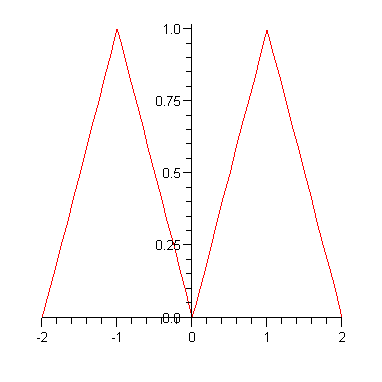
Jatketaan jaksollisena, jaksovälinä [-1,1]. 

> phi:=JJ(phi0,-1..1);
 

proc (x::algebraic) local y; y := floor(1/2*x+1/2); phi0(x-2*y) end proc
proc (x::algebraic) local y; y := floor(1/2*x+1/2); phi0(x-2*y) end proc
proc (x::algebraic) local y; y := floor(1/2*x+1/2); phi0(x-2*y) end proc
proc (x::algebraic) local y; y := floor(1/2*x+1/2); phi0(x-2*y) end proc
proc (x::algebraic) local y; y := floor(1/2*x+1/2); phi0(x-2*y) end proc 

> plot(phi,-2..2);
 

Plot 

>
 

Määritellään sarjan osasummafunktio: 

> osasumma:=N->sum((3/4)^k*phi(4^k*x),k=0..N);
 

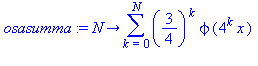
proc (N) options operator, arrow; sum((3/4)^k*phi(4^k*x), k = 0 .. N) end proc 

> osasumma(2);
 

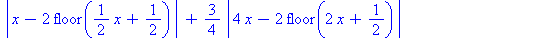
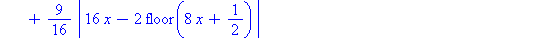
abs(x-2*floor(1/2*x+1/2))+3/4*abs(4*x-2*floor(2*x+1/2))+9/16*abs(16*x-2*floor(8*x+1/2))
abs(x-2*floor(1/2*x+1/2))+3/4*abs(4*x-2*floor(2*x+1/2))+9/16*abs(16*x-2*floor(8*x+1/2)) 

> plot([osasumma(0),osasumma(1),osasumma(2),osasumma(3),osasumma(8)],x=0..1,color=[red,green,blue,black,red]);
 

Plot 

>
 

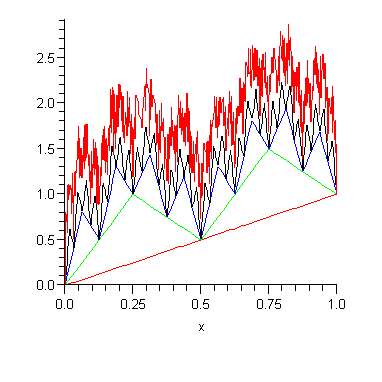
Kuvasta näkyy, miten osasummat muodostuvat. Arvolle N=8 ei kuvan resoluutio enää riitä.  

Lisätään laskentapisteitä ja pienennetään väliä reippaasti: 

> plot(osasumma(8),x=0..0.001,numpoints=800);
 

Plot 

>
 

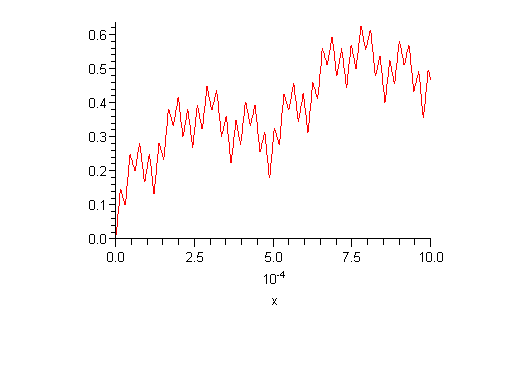
Nytpä alkaa näkyä. 

Katsotaan osasummaa N=10, piennetään edelleen väliä. 

> plot(osasumma(10),x=0..0.0001,numpoints=800);
 

Plot 

>
 

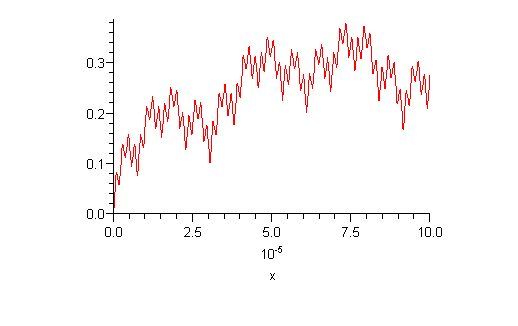
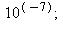Ja kerran vielä. Nyt N=15 ja väliä joudutaan pienentämään jo arvoon 1/10000000; 1.   

> plot(osasumma(15),x=0..0.0000001,numpoints=800);
 

Plot 

>
 

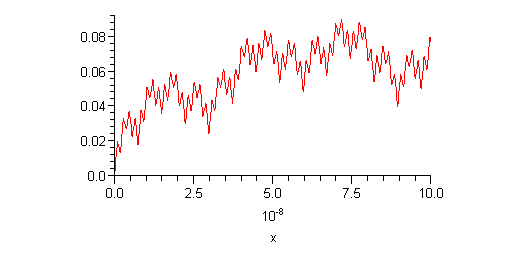
Summa summarum 

 

On helppo uskoa, että näin voidaan jatkaa loputtomasti. Aina, kun otetaan lisää termejä, pitää lisätä laskentapisteitä ja rajoittua yhä pienempään väliin.  

Kuva näyttää aina samanlaiselta. Tässä ilmenee funktion fraktaaliluonne. 

Kuvan perusteella funktio näkyy jatkuvana, mutta miten pienessä ympäristössä tahansa on teräviä kulmia, joten derivaattaa ei ole missään.  

(Tämä ei ole matemaattinen todistus, mutta sen avulla voi jutun juonen ja idean saada paremmin ymmärrettäväksi.)
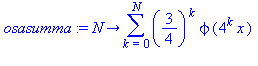