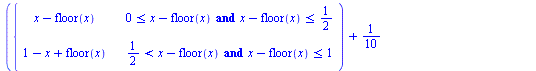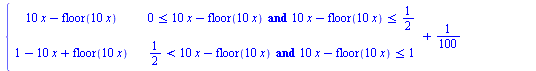Apufunktioita: Jaksollinen jatko: JJ 

Aivan kuten Fourier-sarjoissa, tässä on erinomaisen hyödyllinen väline operaattori, joka suorittaa jaksollisen jatkamisen.  

Hieno toteutus on peräisin  Maple-gurulta: Mike Monaganilta 

>

restart:

 

>	with(plots):

 

>

 

>	# Jaksollinen jatko: MapleTech Vol 3 No. 3 1996 (Mike Monagan) # JJ:=proc(f,d::range)  subs({'F'=f,'L'=lhs(d),'D'=rhs(d)-lhs(d)},  proc(x::algebraic) local y;    y:=floor((x-L)/D);    F(x-y*D);  end) end: # Esim: #sw:=JJ(signum,-1..1); #plot(sw,-4..4); #

 

Määritellään  

>	#g:=x->abs(x-floor(2*x));

 

>	#plot(g,0..1);   # Tässä tulee ikävästi pystyviiva.

 

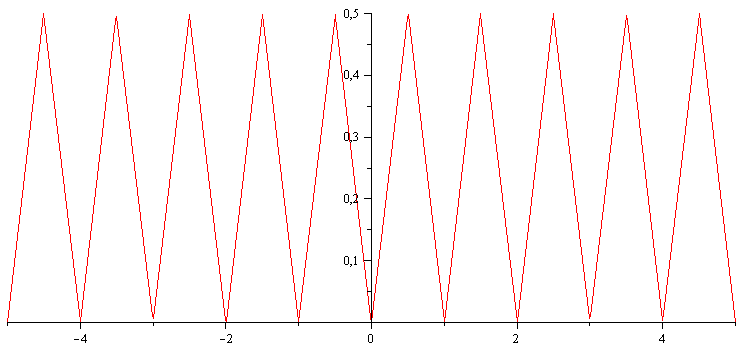
Maplessa voidaan määritellä funktio paloittain. Tässä on selkeä "aaltosulkufunktion" (etäisyys lähimmästä kokonaisluvusta) 

määritelmä välillä [0,1]: 

>	g:=x->piecewise(x >=0 and x <=1/2,x,x>1/2 and x <=1,1-x);

 

(2.1)

 

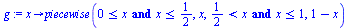>	#plot(g,0..1);

 

>

 

    Jatketaan jaksollisena, jaksovälinä [0,1]. 

>	G:=JJ(g,0..1);

 

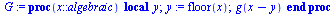(2.2)

 

>	plot(G,-5..5,numpoints=300);

 

>

 

>

 

>

 

Määritellään sarjan osasummafunktio: 

>	osasumma:=N->sum(G((10)^k*x)/10^k,k=0..N);

 

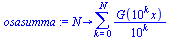(2.3)

 

>	osasumma(2);

 

(2.4)

 

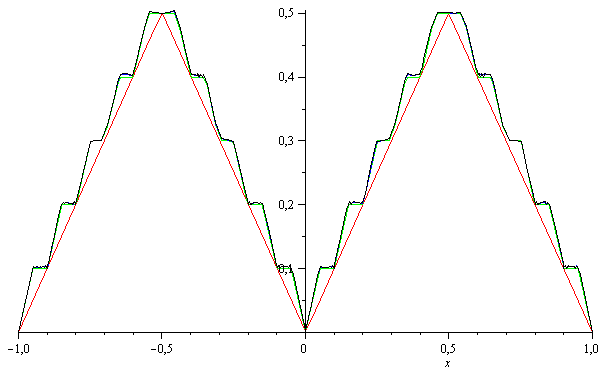
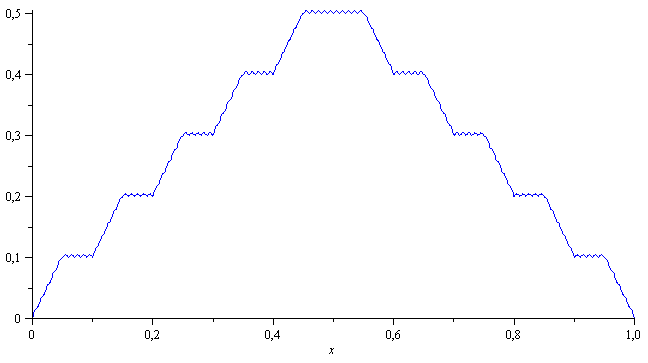
>	plot([osasumma(0),osasumma(1),osasumma(2),osasumma(3)],x=-1..1,color=[red,green,blue,black]);

 

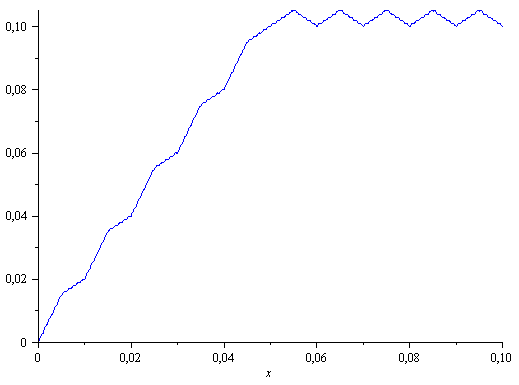
>	plot([osasumma(5),osasumma(10)],x=0..1,numpoints=800,color=[red,blue]);

 

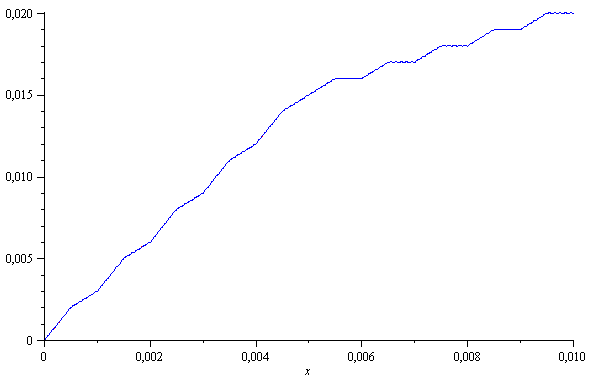
>	plot([osasumma(5),osasumma(10)],x=0..0.1,numpoints=800,color=[red,blue]);

 

>	plot([osasumma(5),osasumma(10)],x=0..0.01,numpoints=800,color=[red,blue]);

 

Kun väliä pienennetään, niin kulmikkuus säilyy. Piirroksissa on otettu osasummat 5 ja 10. Sarja suppenee niin nopeasti, että kuvan tarkkuudella 

eroa ei näy.  

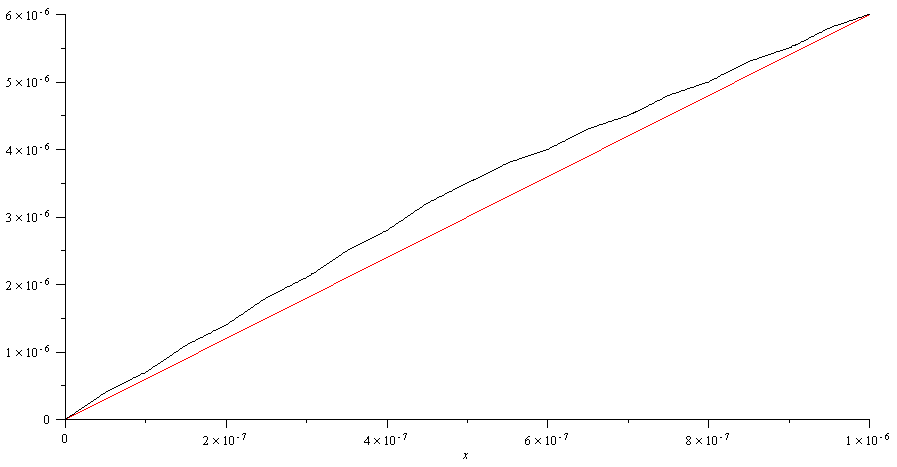
>	plot([osasumma(5),osasumma(10),osasumma(50)],x=0..0.000001,numpoints=800,color=[red,blue,black]);

 

>

 

Jos väliä pienennetään riittävästi, niin osasumma 5 antaa väärän kuvan asiasta. Edellä osasumma 10 riittää, koska osasumma 50 ei muuta kuvaa 

piirroksen tarkkuudella. 

Yksi olennainen piirre on tietysti se, että kyseessä on sarja eikä äärellinen summa. Siten aina, kun x-aluetta piennetään riittävästi, on otettava 

lisää termejä summaan, jotta ilmiö saataisiin näkyviin. 

>