Using SVD for data compression

An example of an unexpected use of linear algebra techniques

Matlab session

help svd

SVD    Singular value decomposition.
  [U,S,V]=SVD(X) produces a diagonal matrix S ..
  ...with nonnegative diagonal elements in
  decreasing order, and unitary matrices U and 
  V so that  X = U*S*V'.
 
close all           
image              % Show the "default image"
[C,Cm] = getframe; % Store it in Matrix C
>> size(C)
ans =
   342   434

What does the matrix look like.
See a portion of it, like rows 25 .. 30 and columns 100..106 .


>> C(25:30,100:106)
ans =
    66    66    66    66    66    66    66
    66    66    66    66    66    66    66
    66    66    66    66    66    66    66
    19    19    19    18    18    18    18
    19    19    19    18    18    18    18
    19    19    19    18    18    18    18

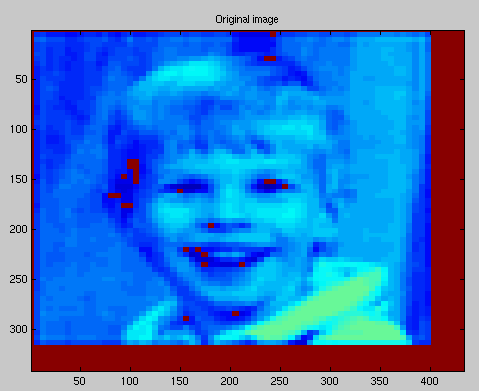
C=flipud(C);  % Turn the matrix upside down, 
%            the original image is upside down
image(C);
title('Original image')

>> tic ; [U,S,V]=svd(C); toc
elapsed_time =
    9.9156  % Time in seconds

figure

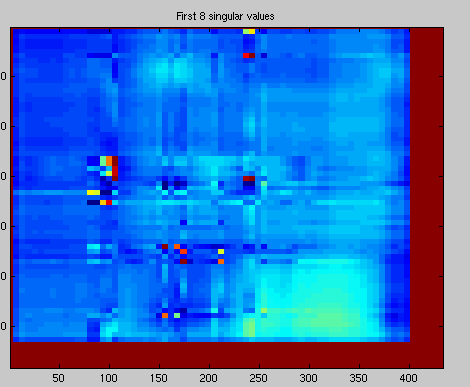
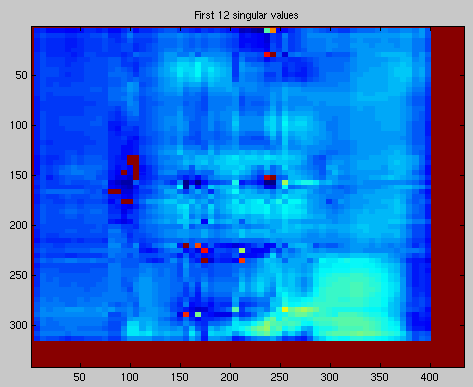
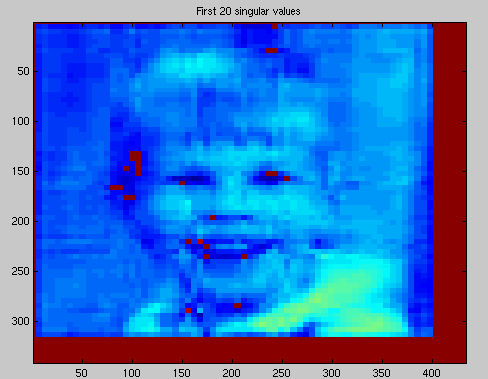
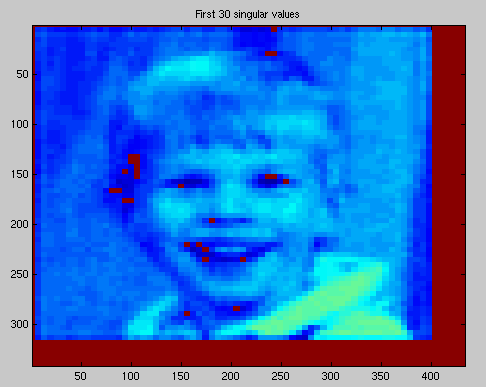
p=30;
M=zeros(size(C));
for i=1:p 
  M=M+S(i,i)*U(:,i)*V(:,i)';
  %figure(i)
  image(M); 
  title(['First ',num2str(i),' singular values'])  
  shg;pause
end;

The images

Some storage issues

>> whos
  Name      Size         Bytes  Class

  C       342x434      1187424  double array
  Cm       67x3           1608  double array
  M       342x434      1187424  double array
  S       342x434      1187424  double array
  U       342x342       935712  double array
  V       434x434      1506848  double array
 


Size of original image (bytes):
>> 342*434*8  
ans =
     1187424   = 1.12 M

Using 30 singular values
>> 342*30*2*8 
ans =
      164160  = 0.16 M

Using 16 singular values
>> 342*16*2*8

ans =
       87552   87 K

image(reshape(1:64,8,8)) % See the colorscale