i ja j
>> help i
I Imaginary unit.
As the basic imaginary unit SQRT(-1), i and j are used to enter
complex numbers. For example, the expressions 3+2i, 3+2*i, 3+2j,
3+2*j and 3+2*sqrt(-1) all have the same value.
Since both i and j are functions, they can be overridden and used
as a variable. This permits you to use i or j as an index in FOR
loops, etc.
See also j.
Muuttujat i ja j edustavat imaginaariyksikköä. Ne eivät kuitenkaan ole
varattuja nimiä. (Itse asiassa ne ovat funktioita, mutta niitä käytetään
muuttujan tavoin.)
>> i
ans =
0 + 1.0000i
>> i=10 % Annetaan i:lle arvo 10.
i =
10
>> clear i % i palautuu oletusarvoonsa.
>> i
ans =
0 + 1.0000i
Huom: Kompleksilukujen esityksessä voidaan käyttää muotoa 3+4i
vain literaalisten vakioiden tapauksessa. Muodot a+ib, a+bi, i4
eivät ole mahdollisia, vaikka muuttujilla a ja b olisi arvot,
koska ib, bi, i4 ovat sallittuja muuttujan nimiä.
Vieno suositus: Käytä aina kertomerkkiä: a+i*b, 2+4*i
>> z=3+4*i z = 3.0000 + 4.0000i >> [real(z) imag(z) abs(z) angle(z) sign(z) conj(z)].' ans = 3.0000 % reaaliosa 4.0000 % im-osa 5.0000 % itseisrvo (moduuli) 0.9273 % vaihekulma (argumentti) 0.5547 + 0.8321i % sign: z/abs(z) 3.0000 - 4.0000i % liittoluku (konjugaatti)Vitsi: Yllä muodostettiin näyttöasun takia vaakavektorin transpoosi. Huomaa
(.') . Pelkkä (') muodostaa konjugoidun transpoosin,
joka konjugoisi (conj(z)):n takaisin. (Tätä käytöstä ei ole tähän mennessä
nähty, kun on käsitelty vain reaalisia matriiseja.)
Esimerkki-istunto kompleksiluvuilla
operoinnista, piirtämisestä, potensseista, ym.
Tässä m-tiedosto, jonka FILE->Publish valinnalla doku generoitui.
Tehtävä
exp(i*pi) , kenen kaava?
>> t=0:pi/50:2*pi; >> z=exp(i*t); >> plot(t,real(z),t,imag(z)) >> figure;plot(z);axis square
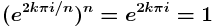
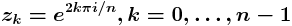
Tehtävä
axis square. Piirrä toiseen ikkunaan (figure) compass-kuva, jossa piirrät nuolet O:sta ao. pisteisiin. Voit myös harjoitella gtext-komentoa
edellisen esimerkkimme tapaan.