Harj. 2 Teht. 5

%{
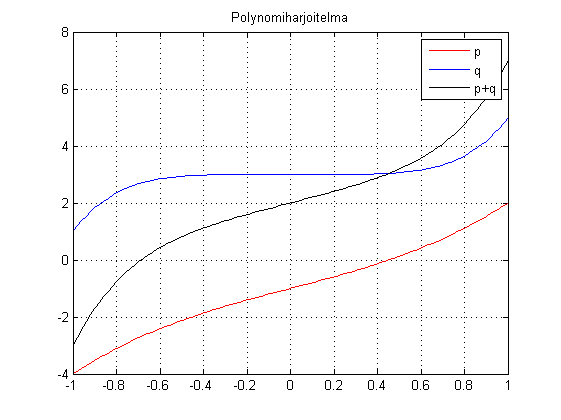
{Muodosta Matlabilla polynomien p(x)= x^3+2x -1  ja q(x)=2x^5+ 3
summa ja määritä sen arvo vektorin -1:0.5:1 pisteissä.
Piirrä kuvaaja, jossa on p,q ja p+q sopivalla välillä.
%}
clear  % Poistetaan muuttujat
close all  % Suljetaan kaikki grafiikkaikkunat.
format compact  % Tulostus tiiviiksi.
p=[1 0 2 -1]
q=[2 0 0 0 0 3]

s=[0 0 p]+q  % Vektorit saatetaan yhtä pitkiksi etunollilla.

polyval(p,0)+polyval(q,0)
polyval(s,0)

x=-1:0.5:1;
px=polyval(p,x);
qx=polyval(q,x);
sx=polyval(s,x);

max_ero=max(abs(px+qx-sx)) % Ei ihan riitä, yksi piste lisää.
                           % Saat hoitaa itse.
% Piirtämiseen tarvitaan enemmän pisteitä.

x=linspace(-1,1);
px=polyval(p,x);   % Huomaa: nämä on nyt laskettava
qx=polyval(q,x);   % uudestaan, kun x muutettiin.
sx=polyval(s,x);

plot(x,px,'r',x,qx,'b',x,sx,'k')
title('Polynomiharjoitelma')
legend('p','q','p+q')
grid on

p =
     1     0     2    -1
q =
     2     0     0     0     0     3
s =
     2     0     1     0     2     2
ans =
     2
ans =
     2
max_ero =
     0