Ratkaisuja (valikolituihin) tehtäviin 1
25.5.2010
Contents
Teht 1
clear % Puhdistetaan työtila vanhoista muuttujista. x = [1 2 3 4 5]; % Puolipisteisiin on hyvä tottua. y = [0 2 4 6]; z = [-4 -2 0 2 4 ]; who % Katsotaan työtilan muuttujat. format compact % Tiivistetty tulostusmuoto x % Kirjoittamalla muttujan nimen, näet sen sisällön. x,y,z % Komentoja voidaan antaa samalla rivillä pilkulla tai % puolipisteellä erotettuna. why % Leikitään vähän (Moler-huumoria) % Jos haluat tutustua jo nyt Matlab-ohjelmointiin, sano: type why
Your variables are:
x y z
x =
1 2 3 4 5
x =
1 2 3 4 5
y =
0 2 4 6
z =
-4 -2 0 2 4
Can you rephrase that?
length(x),length(y),length(z) x.*z % Pisteittäinen kertolasku, onneksi x ja z samanpituiset. x'*z % Ulkotulo: Matriisi: (x(i)*z(j)). Ei tarvitse olla samanpituiset. % Parempi olisi ollut tässä pyytää x'*y % ja/tai y'*x % x*x' on x:n sisätulo itsensä kanssa, eli koordinaattien neliösumma. % norm(x,2) laskee saman (Euklidinen normi). Norm-funktion oletusarvona % on 2-normi. Kts. help norm x.^2 % Pisteittäinen potenssi; koordinaatit korotetaan toiseen. 'x^2' % Matriisipotenssi, tässä x*x, mahdollinen vain neliömatriisille.
ans =
5
ans =
4
ans =
5
ans =
-4 -4 0 8 20
ans =
-4 -2 0 2 4
-8 -4 0 4 8
-12 -6 0 6 12
-16 -8 0 8 16
-20 -10 0 10 20
ans =
0 2 4 6
0 4 8 12
0 6 12 18
0 8 16 24
0 10 20 30
ans =
0 0 0 0 0
2 4 6 8 10
4 8 12 16 20
6 12 18 24 30
ans =
1 4 9 16 25
ans =
x^2
Teht 2.
clear % Tyhjennetään vanhoista muuttujista (selkeyttää). u=[3;4;5;6]; v=[0;2;4;6]; u,v % Tai: u=(3:6)', v=(0:2:6)' % c,b,a voidaan rakentaa monilla tavoilla, tietysti ihan kirjoittamalla % alkio kerrallaan tyyliin: c=[1 2 3;1 3 6;1 4 9] % Muita tapoja: c=[ones(3,1) (2:4)' (3:3:9)'] % tai c=[(1:3);1 3 6;1 4 9] a=[1:4;5:8;9:12] % tai a=reshape(1:12,3,4) b=[3:6;2:-1:-1;5 4 2 0;1 2 1 1]
u =
3
4
5
6
v =
0
2
4
6
u =
3
4
5
6
v =
0
2
4
6
c =
1 2 3
1 3 6
1 4 9
c =
1 2 3
1 3 6
1 4 9
c =
1 2 3
1 3 6
1 4 9
a =
1 2 3 4
5 6 7 8
9 10 11 12
a =
1 4 7 10
2 5 8 11
3 6 9 12
b =
3 4 5 6
2 1 0 -1
5 4 2 0
1 2 1 1
Teht 3
n=4;k=3; In=eye(n,n); Ynk=ones(n,k); Nnk=zeros(n,k); Ik=eye(k,k);Nn=zeros(n,n); A=[In Ynk;Nnk' Ik] B=[Nn In;-In Nn]
A =
1 0 0 0 1 1 1
0 1 0 0 1 1 1
0 0 1 0 1 1 1
0 0 0 1 1 1 1
0 0 0 0 1 0 0
0 0 0 0 0 1 0
0 0 0 0 0 0 1
B =
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
-1 0 0 0 0 0 0 0
0 -1 0 0 0 0 0 0
0 0 -1 0 0 0 0 0
0 0 0 -1 0 0 0 0
Teht 3.5
% a) % v(end:-1:1) % Vektori % A(:,end:-1:1) % Matriisin sarakkeet % A(end:-1:1,:) % Matriisin rivit type fliplr %type flipud % b) u=1:7 v=-u N=length(u); u_alle_v = [u;v] limitetty=u_alle_v(:)'
function y = fliplr(x)
%FLIPLR Flip matrix in left/right direction.
% FLIPLR(X) returns X with row preserved and columns flipped
% in the left/right direction.
%
% X = 1 2 3 becomes 3 2 1
% 4 5 6 6 5 4
%
% Class support for input X:
% float: double, single
%
% See also FLIPUD, ROT90, FLIPDIM.
% Copyright 1984-2004 The MathWorks, Inc.
% $Revision: 5.9.4.3 $ $Date: 2004/07/05 17:01:14 $
if ndims(x)~=2
error('MATLAB:fliplr:SizeX', 'X must be a 2-D matrix.');
end
y = x(:,end:-1:1);
u =
1 2 3 4 5 6 7
v =
-1 -2 -3 -4 -5 -6 -7
u_alle_v =
1 2 3 4 5 6 7
-1 -2 -3 -4 -5 -6 -7
limitetty =
1 -1 2 -2 3 -3 4 -4 5 -5 6 -6 7 -7
Teht. 4 ja 6
A=magic(5) sarakesummat=sum(A) % tai: sum(A,[1]) rivisummat=sum(A') % tai sum(A,[2]) lavistajasumma=sum(diag(A)) sivulavistajasumma=sum(diag(fliplr(A))) [ov,oa]=eig(A) V=ov;D=oa; IV=inv(V); A,V*D*IV A-V*D*IV % A:n diagonalisointi A=V*D*inv(V) %{ Koska rivisummat = vakio = 65, niin yksi ominaisvektori on v=[1 1 1 1 1]', sillä A*v = [65;65;65;65;65] = 65*[1;1;1;1;1] = 65*v. Laskemalla nähdään, että muut ovat pienempiä. Normeerataan luvulla 65 näin: A = 65*V*D/65*inv(V) Merkitään D1=D/65 D1 on diagonaalimatriisi, jonka (itseisarvoltaan) suurin alkio = 1, muut ovat aidosti pienempiä. Nyt A^k = 65^k * V * D1^k * inv(V). Jos diagonaalimatriisilla kerrotaan vasemmalta jokin matriisi C, niin C:n rivit tulevat kerrotuiksi diagonaalialkioilla. Mieti kynää ja paperia käyttäen, voithan kokeilla myös Matlabilla vaikka tyyliin: C=reshape(1:9,3,3)',Dm=diag(-1:1), Dm*C, C*Dm Oikelta kerrottaessa kerrotaan vastaavasti sarakkeet, kuten laskukin vahvistaa. No, muodostetaan D1:n potensseja: %} format long D1=D/65; k=1,Dk=D1 k=k+1, Dk=Dk*Dk % toista nuolinäppäimellä k=k+1, Dk=Dk*Dk k=k+1, Dk=Dk*Dk k=k+1, Dk=Dk*Dk %{ Arvolla k=6 tulee Matlabin laskentatarkkuudella diagonaalimatriisi: diag([1 0 0 0 0]), joten D1^k*inv(V) on matriisi, jossa 1. vaakarivi on inv(V):n eka vaakarivi, loput ovat nollarivejä. Matriisin rangi on siten 1, ja se ei siitänsä kasva kerrottaessa vasemmalta millä tahansa matriisilla. (Jos tässä oli vieraita lineaarialgebran käsitteitä, niin älä huoli, muistetele näitä laskuja lämmöllä sitten, kun noihin törmäät.) %}
A =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
sarakesummat =
65 65 65 65 65
ans =
65 65 65 65 65
rivisummat =
65 65 65 65 65
ans =
65
65
65
65
65
lavistajasumma =
65
sivulavistajasumma =
65
ov =
-0.447213595499958 0.097640070932979 -0.632976910516003 0.678009723956060 -0.261860649935008
-0.447213595499958 0.352538557500108 0.589480807113999 0.322279530272055 -0.173165093661345
-0.447213595499958 0.550110625795028 -0.391529640194349 -0.550110625795028 0.391529640194349
-0.447213595499958 -0.322279530272056 0.173165093661345 -0.352538557500107 -0.589480807113999
-0.447213595499958 -0.678009723956059 0.261860649935008 -0.097640070932980 0.632976910516004
oa =
65.000000000000043 0 0 0 0
0 -21.276765471473812 0 0 0
0 0 -13.126280930709234 0 0
0 0 0 21.276765471473780 0
0 0 0 0 13.126280930709219
A =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
ans =
17.000000000000025 24.000000000000021 1.000000000000018 8.000000000000014 15.000000000000018
23.000000000000028 4.999999999999996 7.000000000000024 14.000000000000025 16.000000000000021
4.000000000000025 6.000000000000012 12.999999999999991 20.000000000000000 22.000000000000011
10.000000000000021 12.000000000000012 18.999999999999996 20.999999999999993 3.000000000000002
11.000000000000016 18.000000000000018 24.999999999999996 1.999999999999985 8.999999999999998
ans =
1.0e-13 *
-0.248689957516035 -0.213162820728030 -0.182076576038526 -0.142108547152020 -0.177635683940025
-0.284217094304040 0.044408920985006 -0.239808173319034 -0.248689957516035 -0.213162820728030
-0.248689957516035 -0.115463194561016 0.088817841970013 0 -0.106581410364015
-0.213162820728030 -0.124344978758018 0.035527136788005 0.071054273576010 -0.017763568394003
-0.159872115546023 -0.177635683940025 0.035527136788005 0.150990331349021 0.017763568394003
k =
1
Dk =
1.000000000000001 0 0 0 0
0 -0.327334853407289 0 0 0
0 0 -0.201942783549373 0 0
0 0 0 0.327334853407289 0
0 0 0 0 0.201942783549373
k =
2
Dk =
1.000000000000001 0 0 0 0
0 0.107148106255172 0 0 0
0 0 0.040780887827669 0 0
0 0 0 0.107148106255171 0
0 0 0 0 0.040780887827669
k =
3
Dk =
1.000000000000003 0 0 0 0
0 0.011480716674070 0 0 0
0 0 0.001663080812013 0 0
0 0 0 0.011480716674069 0
0 0 0 0 0.001663080812013
k =
4
Dk =
1.000000000000005 0 0 0 0
0 0.000131806855350 0 0 0
0 0 0.000002765837787 0 0
0 0 0 0.000131806855350 0
0 0 0 0 0.000002765837787
k =
5
Dk =
1.000000000000011 0 0 0 0
0 0.000000017373047 0 0 0
0 0 0.000000000007650 0 0
0 0 0 0.000000017373047 0
0 0 0 0 0.000000000007650
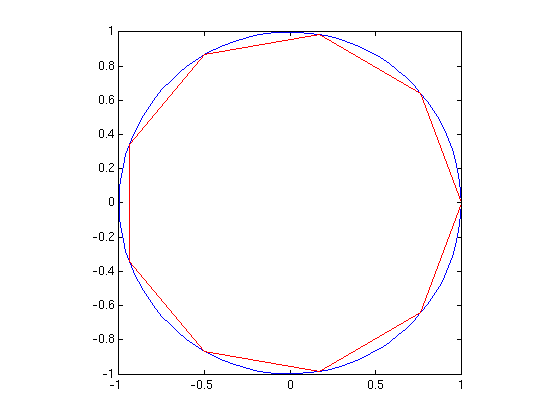
Tehtävä 5.
t=linspace(0,2*pi);x=cos(t);y=sin(t);plot(x,y) axis equal; axis square hold on;t=linspace(0,2*pi,10);x=cos(t);y=sin(t);plot(x,y,'r')