Contents

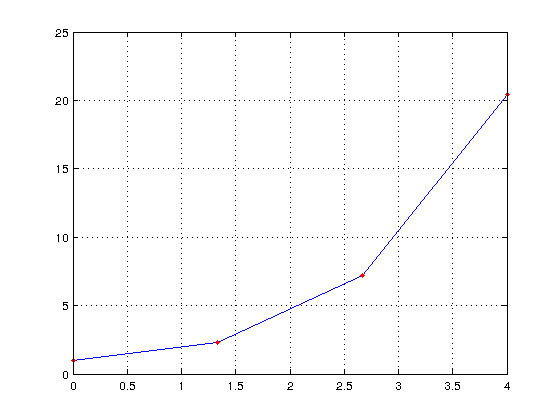
% lyhyt/euleresim1.m
% Eulerin menetelma: alkuarvoteht: y'=t+y, y(0)=1
% "Nuolinappainversio", havainnollistus
% Lineaarinen epahomogeeninen, tarkka ratkaisu:
%              y(t)=2exp(t) - t -1


clear; close all
% y'=t+y, y(0)=1, ratk. valilla [0,1.2]

f=@(t,y)t+y

YL=[]   % Talletetaan lasketut arvot valin loppupisteessa
n=3;
[T,Y]=eulerS(f,[0 4],1,n); [T Y],plot(T,Y,T,Y,'.r');shg;YL=[YL Y(end)]
grid on; hold on

f = 
    @(t,y)t+y
YL =
     []
ans =
         0    1.0000
    1.3333    2.3333
    2.6667    7.2222
    4.0000   20.4074
YL =
   20.4074

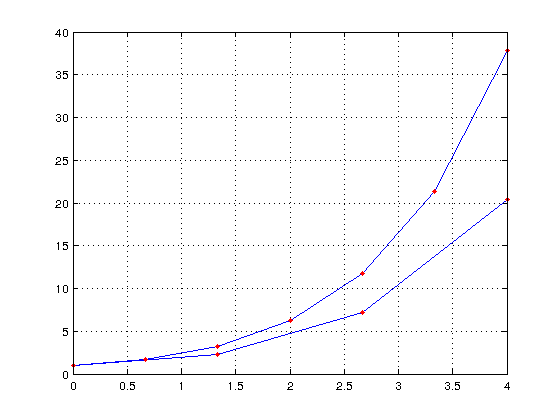
Suorita tata rivia nuolinappainiteroiden komentoikkunassa tai

mieluumminkin CTR-ENTER Matlab-editorissa:

n=2*n,[T,Y]=eulerS(f,[0 4],1,n); [T Y];plot(T,Y,T,Y,'.r');shg;YL=[YL Y(end)]

n =
     6
YL =
   20.4074   37.8669

Iteroinnin jalkeen:

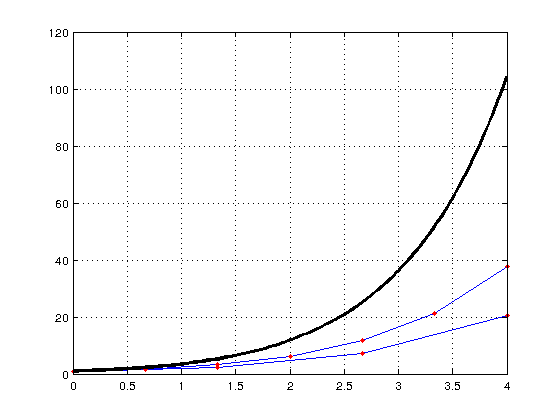
ytarkka=@(t) 2*exp(t)-t-1;

t=linspace(0,4);
plot(t,ytarkka(t),'k','LineWidth',3);shg

%fplot(ytarkka,[0 4],'--rs','LineWidth',2)  %plot-optiot
                                        %ei kaikki toimi fplot:lla

format compact
['Loppupiste Tarkka ratk.  Euler-approksimaatio']
[T(end) ytarkka(T(end)) YL(end)]

virheetloppupisteesa=ytarkka(T(end))-YL

ans =
Loppupiste Tarkka ratk.  Euler-approksimaatio
ans =
    4.0000  104.1963   37.8669
virheetloppupisteesa =
   83.7889   66.3294

Published with MATLAB® R2013a