Contents

Stabiili/epästabiili diffyhtälö

  5.6.2012 Heikki Apiola

%{
Havinnollistetaan epästabiilisuutta Alkuarvotehtävillä
 y'=y, y(0)=c   (Tarkka ratkaisu y(t)=c*exp(t) )
 y'=-y, y(0)=c  (Tarkka ratk.  y(t)=c*exp(-t) )
Ratkaistaan Matlabin ode45-funktiolla, kertalukuja 4 ja 5 yhdistelevällä
Runge-Kutta-Fehlberg-menetelmällä.
%}
clear
close all

y'=y, epästabiili tapaus

F=@(t,y)y
[T,Y]=ode45(F,[0 5],0);
[T,Y0]=ode45(F,[0:.1:5],0.1);
[T,Y1]=ode45(F,[0:.1:5],0);
[T,Y2]=ode45(F,[0:.1:5],-0.1);
plot(T,Y0,T,Y1,T,Y2)
grid on
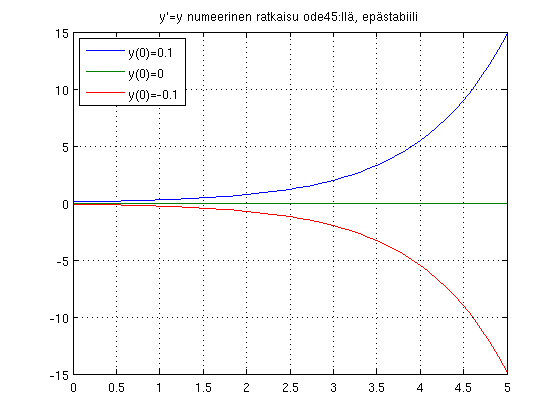
title('y''=y numeerinen ratkaisu ode45:llä, epästabiili')
legend('y(0)=0.1','y(0)=0','y(0)=-0.1','Location','NorthWest')

disp('Hyvin pieni muutos alkuarvossa aiheuttaa suuren muutoksen tulevaisuudessa.')
disp('Yhtälö on erittäin epästabiili.')

F = 

    @(t,y)y

Hyvin pieni muutos alkuarvossa aiheuttaa suuren muutoksen tulevaisuudessa.
Yhtälö on erittäin epästabiili.

y'=-y, stabiili tapaus

F=@(t,y)-y
[T,Y]=ode45(F,[0 5],0);
[T,Y0]=ode45(F,[0:.1:5],1);
[T,Y1]=ode45(F,[0:.1:5],0);
[T,Y2]=ode45(F,[0:.1:5],-1);
figure
plot(T,Y0,T,Y1,T,Y2)
grid on
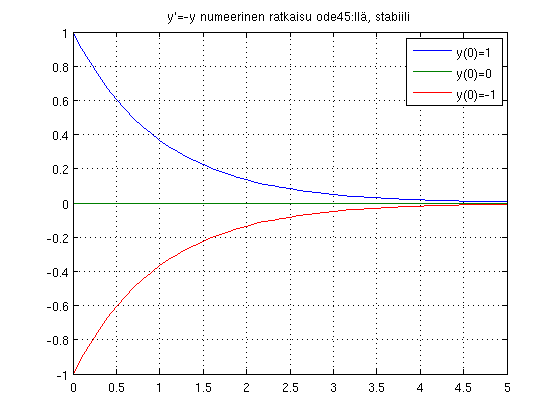
title('y''=-y numeerinen ratkaisu ode45:llä, stabiili')
legend('y(0)=1','y(0)=0','y(0)=-1','Location','NorthEast')

% Suurikin muutos alkuarvoissa johtaa melkein samaan "ennusteseen".

F = 

    @(t,y)-y

Published with MATLAB® 7.14