Abstract
The purpose is to teach linear mappins, their geometric meaning in the plane and especially the geometric idea of eigenvalues/eigenvectors.
The worksheet contains several animations. They should be run by clicking the plot (the initial frame),
which gives the
user an animation toolbar. The most useful tool is perhaps the slider. This requires you to have
Maple (or at least Maple reader (?)).
There is an html-export: ominaisarvot.html (this file). In this case no user interaction is possible, animations are running continuously, but nevertheless these examples might be useful in aquiring a geometric view for the basics of eigenvector theory.
The rest of the explanations and comments are in Finnish (for the time being).
Alustukset
| > |
restart: |
| > |
with(LinearAlgebra):
with(linalg): |
| > |
with(plots):setoptions(scaling=constrained):setoptions3d(axes=boxed,orientation=[-30,50]):
|
| > |
alias(Inv=MatrixInverse,Id=IdentityMatrix,Diag=DiagonalMatrix,Tr=Transpose): |
| > |
alias(rref=ReducedRowEchelonForm):alias(ref=GaussianElimination):
alias(Id=IdentityMatrix): |
Määritellään apufunktioita.
Ovat kertakäyttöluonteisia, helposti lennossa modifioitavia.
1. Muotoa [xdata ]
[ydata ]
olevan matriisin määräämien pisteiden polygonipiirto Vastaa Matlabin plot(xdata,ydata) - komentoa.
| > |
piirraM:=dataM->plot(convert(Transpose(dataM),listlist),axes=box,scaling=constrained): |
| > |
piirraMb:=dataM->plot(convert(Transpose(dataM),listlist),color=blue,axes=box): # Sama sinisellä (värin olis voinut laittaa lisäargumentiksi, mutta näin on vähemmän koodia.) |
| > |
piirraMr:=dataM->plot(convert(Transpose(dataM),listlist),color=red,axes=box): # Varmuudeksi vielä punaisella, vaikka onkin oletus. |
Yllä olevat sopivat erilaisten alueiden kuvautumistehtäviin.
Seuraavaksi katsotaan yksittäisten vektorien kuvautumista, erityisesti ominaisvektorihavainnollistuksiin.
Funktio plots[arrow] mahdollistaa hyvin mainion helpon tavan nuolikuvioon, jossa sinisellä annetaan lähtönuoli ja punaisella sen kuvanuoli, kas näin:
| > |
kuvakulma:=(A,u)->display(arrow(u,shape=arrow,color=blue),arrow(A.u,shape=arrow,color=red),scaling=constrained,title="Lahto:sininen, kuva:punainen"): |
Haluamme katsoa kuvauksen dynamiikkaa animaationa, se käy taas kuin unelma. Jaetaan täyskulma n:ään osaan ja jokaista kohti piirretään sininen yksikkövektori ja sen punainen kuva. Ajetaan animaationa (insequence=true).
| > |
nuoletAni:=(A,n)->display(seq(kuvakulma(A,<cos(Theta),sin(Theta)>),Theta=[seq(kkk*2*Pi/n,kkk=0..n)]),insequence=true,scaling=constrained): |
Joskus on mukavaa (ainakin esteettisesti) katsoa kuvaa staattisesti jättäen kaikki nuolet kuvaan mukaan. Muuten sama, mutta "insequence=false"
| > |
nuolikimppu:=(A,n)->display(seq(kuvakulma(A,<cos(Theta),sin(Theta)>),Theta=[seq(kkk*2*Pi/n,kkk=0..n)]),insequence=false,scaling=constrained): |
Lineaarikuvaukset tasossa ja niiden havannollistaminen
Monikulmion kuvautuminen
Kokeillaan määrittelemiämme funktioita:
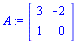 |
(3.1.1) |
| > |
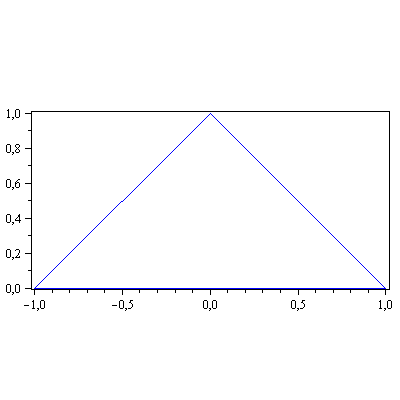
kolmio:=<<-1,0>|<1,0>|<0,1>|<-1,0>>; |
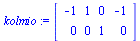 |
(3.1.2) |
| > |
S:=A.kolmio; # Kolmion kuva kuvauksessa A. |
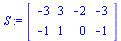 |
(3.1.3) |
| > |
display(array([[piirraMb(kolmio),piirraMr(S)]])); |
| > |
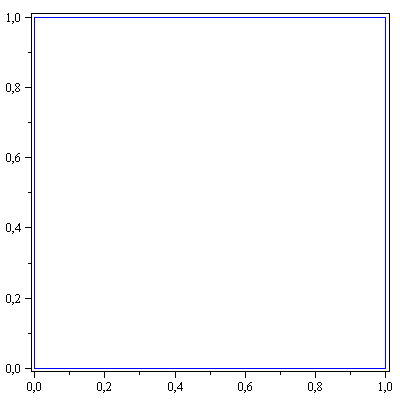
nelio:=<<0,0>|<1,0>|<1,1>|<0,1>|<0,0>>; |
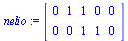 |
(3.1.4) |
| > |
display(array([[piirraMb(nelio),piirraMr(A.nelio)]])); |
| > |
#piirraMb(nelio);piirraM(A.nelio); # Yksitellen piirto antaa isomman ja muokattavan kuvan (tehdään tilanteen mukaan). |
| > |
N:=50: h:=2*Pi/N:t:=seq(k*h, k=1..N+1):x:=map(cos,[t]): y:=map(sin,[t]): |
| > |
ympyra:=Matrix([x,y]): # Matlab-tyylinen ympyrä |
| > |
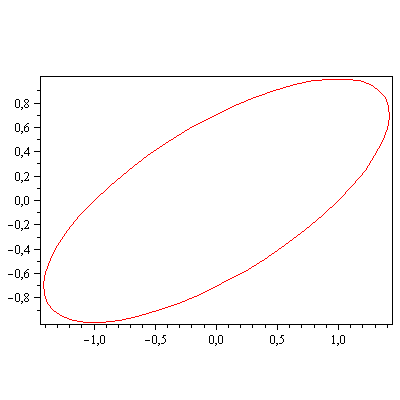
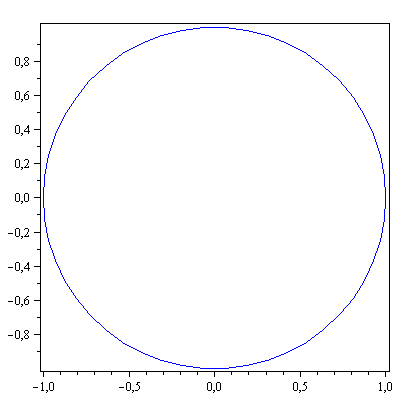
piirraMb(ympyra);
>piirraM(A.ympyra); |
Ympyrän kuva näyttää ellipsiltä, onkohan näin aina?
Strangin talo
Gilbert Strang: An Introduction to Linear Algebra, kts, myös MIT-luentoja)
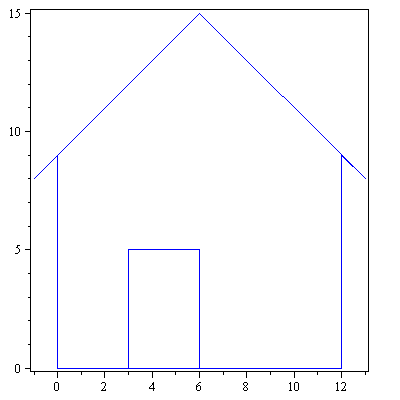
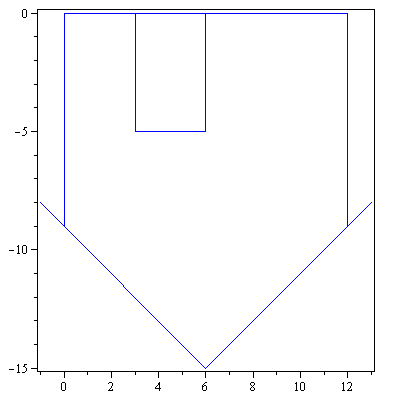
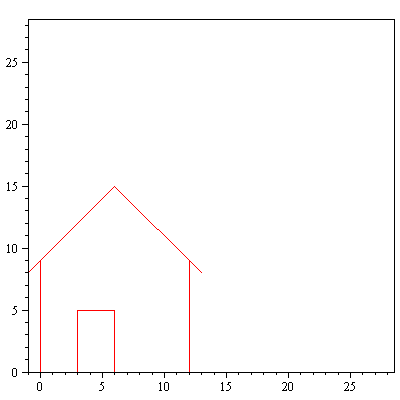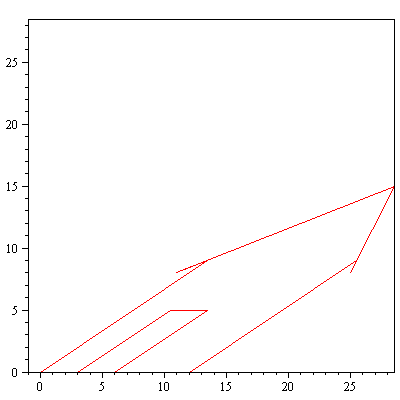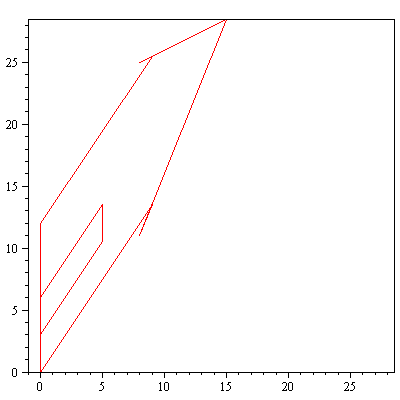
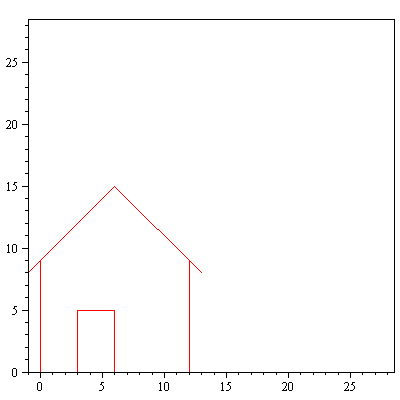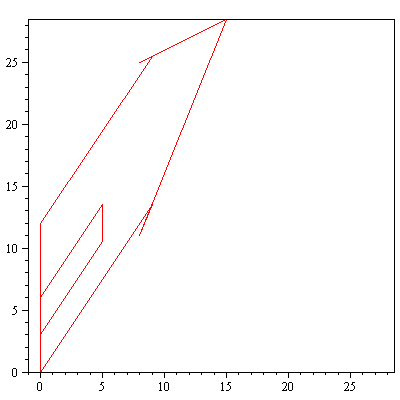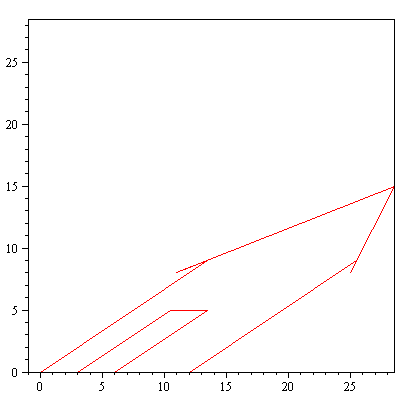
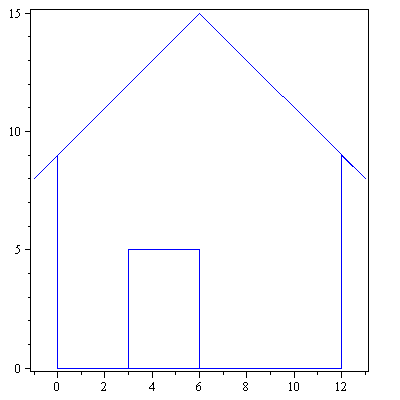
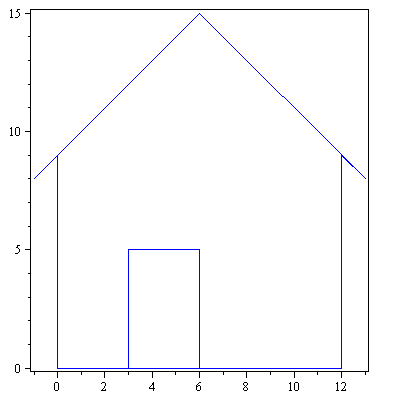
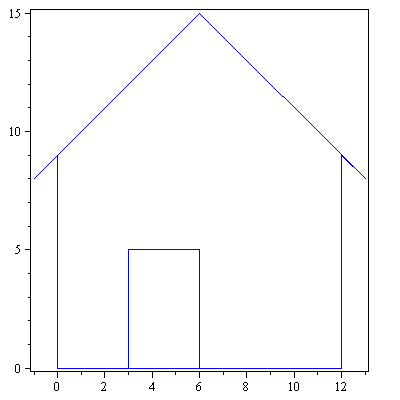
Ympyröiden, kolmioiden, neliöiden ym. lisäksi "Strangin talo" on hyvä esimerkkikuvio linaarikuvausten havainnollistamisessa.
>
talo:=Tr(<<0,0,-1,6,13,12,12,3,3,6,6,0>|<0,9,8,15,8,9,0,0,5,5,0,0>>):
> piirraMb(talo);
| > |
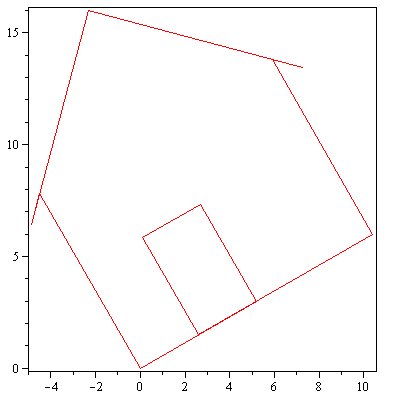
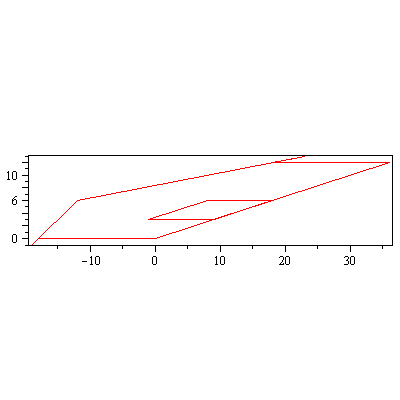
display(array([[piirraMb(talo),piirraMr(A.talo)]])); |
Geometrisin kuvauksin annettuja lineaarikuvauksia
1. Peilaus x-akselin suhteen:
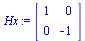 |
(3.3.1) |
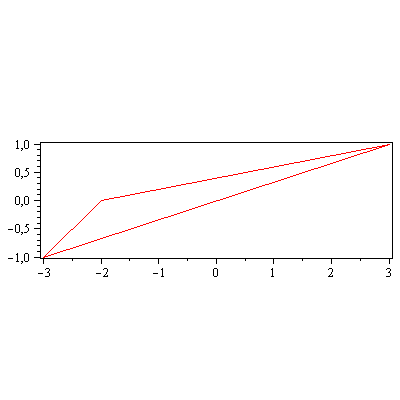
2. Peilaus suoran y=x suhteen
| > |
Hyy_on_x:=<<0,1>|<1,0>>; |
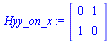 |
(3.3.2) |
| > |
kolmio:=<<0,0>|<1,1>|<0,1>|<0,0>>: |
| > |
#piirraMb(kolmio);piirraM(Hyy_on_x.kolmio);#piirraM(Hy.(Hy.kolmio)); |
| > |
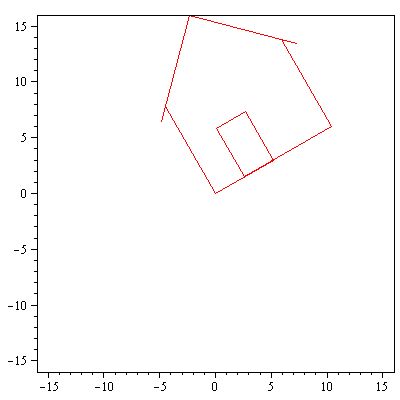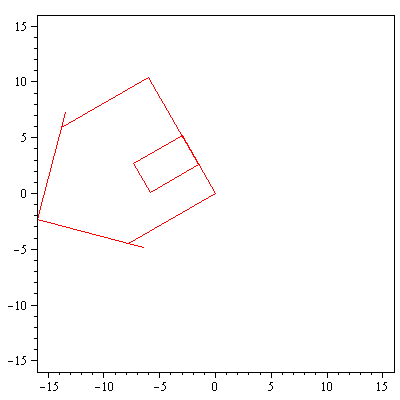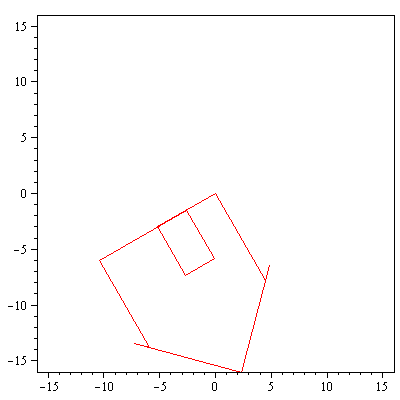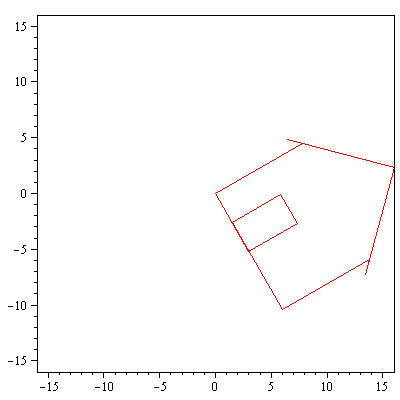
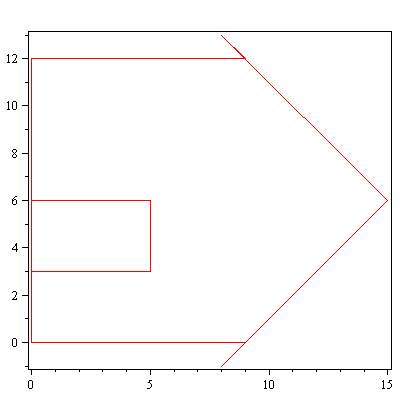
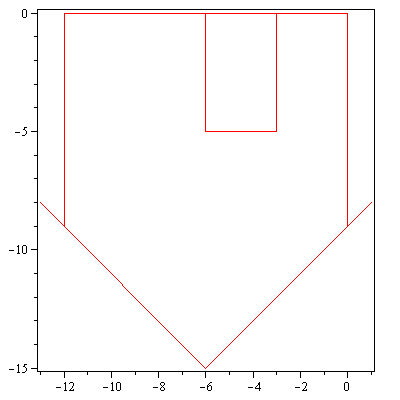
display(array([[piirraMb(talo),piirraMr(Hyy_on_x.talo)]])); |
3. Peilaus O:n suhteen
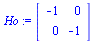 |
(3.3.3) |
| > |
display(array([[piirraMb(talo),piirraMr(Ho.talo)]])); |
4. Vaakasuora skaalaus
| > |
d:='d':Svaaka:=<<d,0>|<0,1>>; |
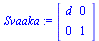 |
(3.3.4) |
| > |
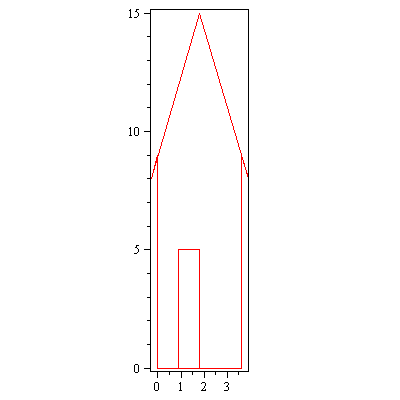
d:=0.3:piirraMr(Svaaka.talo); |
| > |
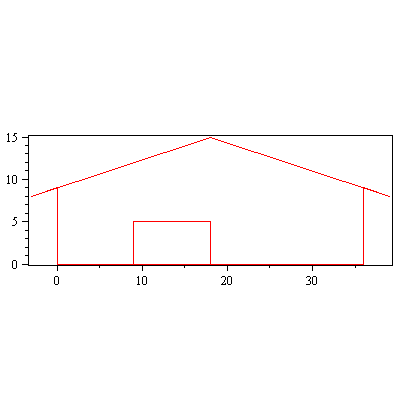
d:=3:piirraMr(Svaaka.talo); |
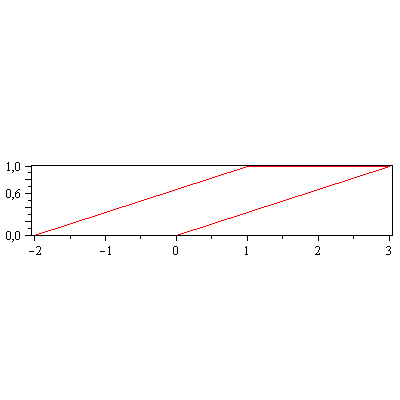
Horizontal shear
| > |
Shearx:=k-><<1,0>|<k,1>>; |
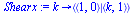 |
(3.3.5) |
| > |
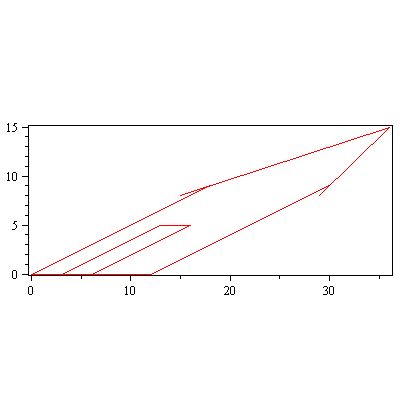
piirraM(Shearx(2).talo); |
Projektio x-akselille
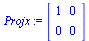 |
(3.3.6) |
Kierto
| > |
Kierto:=alpha-><<cos(alpha),sin(alpha)>|<-sin(alpha),cos(alpha)>>; |
 |
(3.3.7) |
| > |
piirraM(Kierto(Pi/6).talo); |
| > |
display(seq(piirraM(Kierto(Pi/6)^k.talo),k=1..10),insequence=true); |
Yhdistelmiä
a) Iteroidaan "shear"-kuvausta
| > |
display(seq(piirraM(Shearx(1.2)^k.talo),k=0..6),insequence=true); |
| > |
A[1]:=talo: A[2]:=Shearx(1.5).talo: A[3]:=Hyy_on_x.A[2]: |
| > |
display(seq(piirraM(A[k]),k=1..3),insequence=true); # Tehdään sama toisessa järjestyksessä |
| > |
display(seq(piirraM(A[k]),k=[1,3,2]),insequence=true); |
Samat lineaarikuvaukset eri järjestyksessä tuottavat eri tuloksen.
Ominaisvektoreiden (ja -arvojen) havainnollistusta nuolikuvin
Yllä määritelty kuvakulma ja siihen pohjautuva nuoletAni (ja nuolikimppu) ovat nyt onnen omiaan.
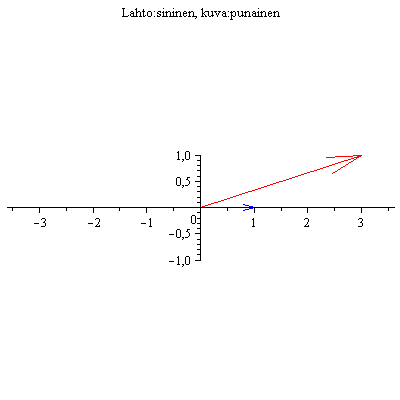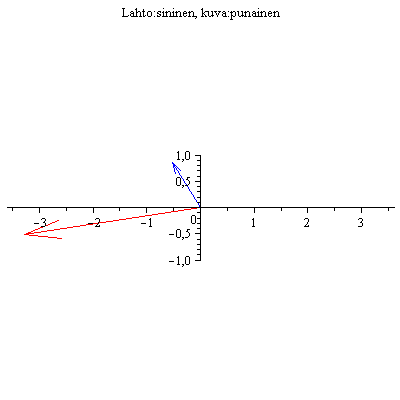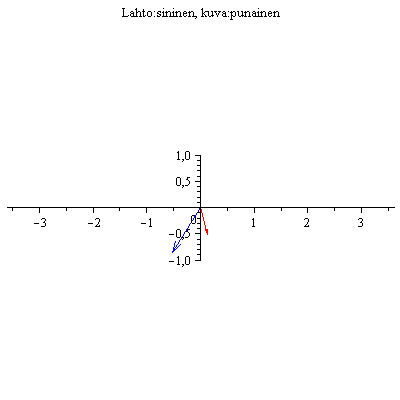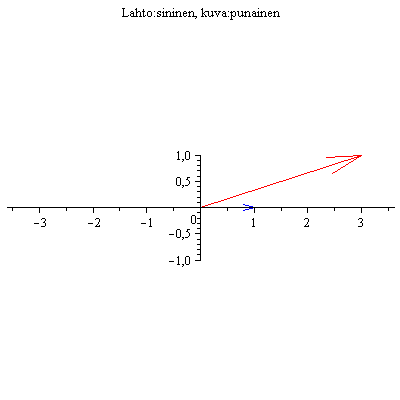
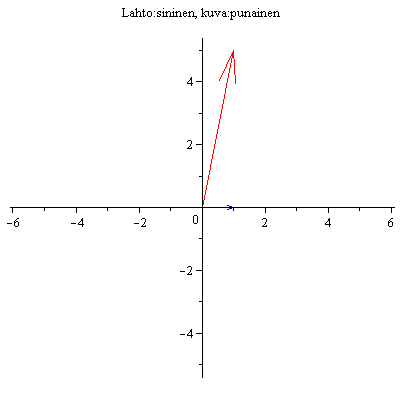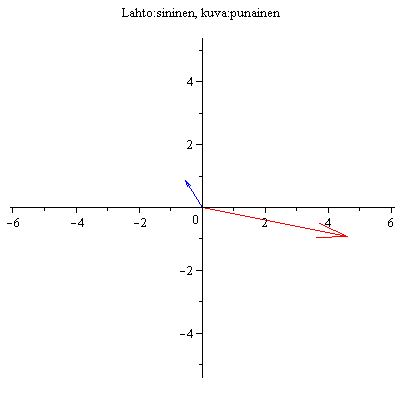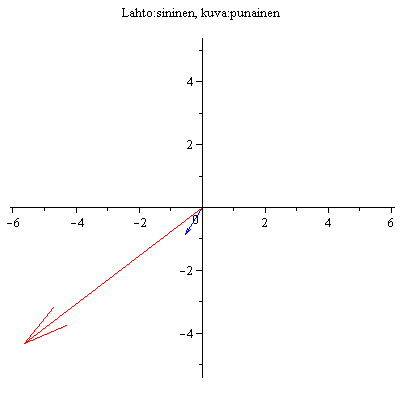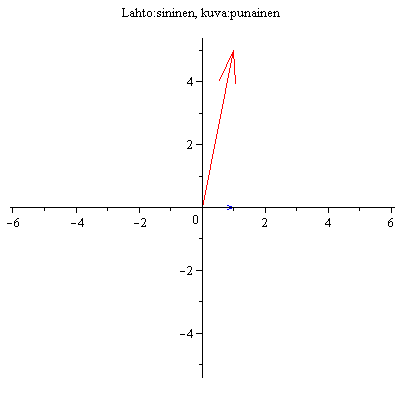
Esim 1.
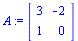 |
(4.1) |
](images/ominaisarvot_40.gif) |
](images/ominaisarvot_41.gif) |
(4.2) |
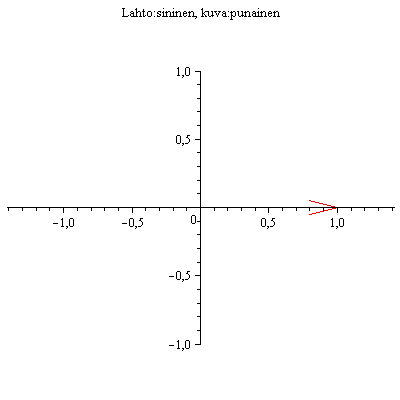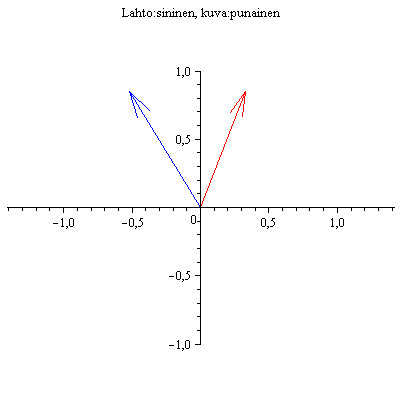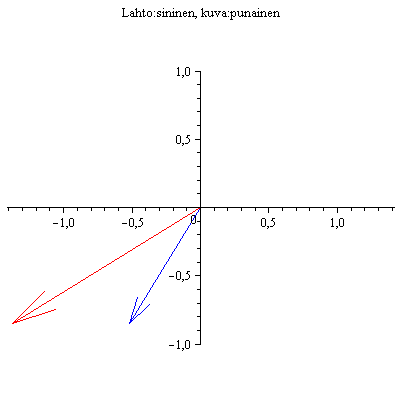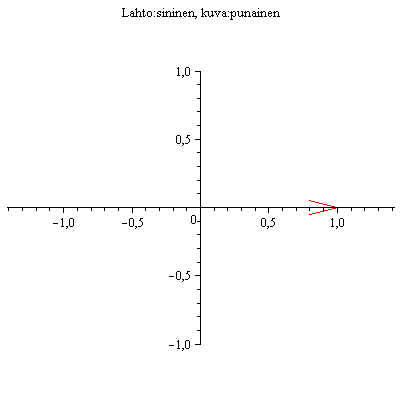
Valitaan toinen lähtöpiste
](images/ominaisarvot_43.gif) |
](images/ominaisarvot_44.gif) |
(4.3) |
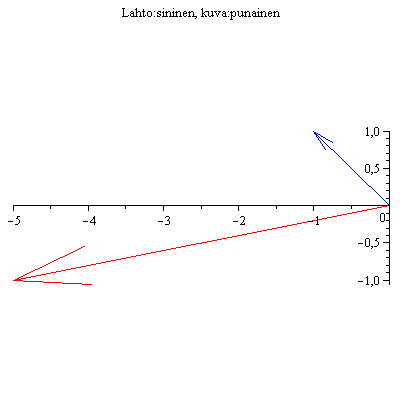
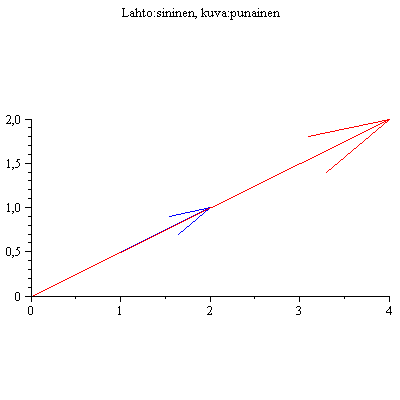
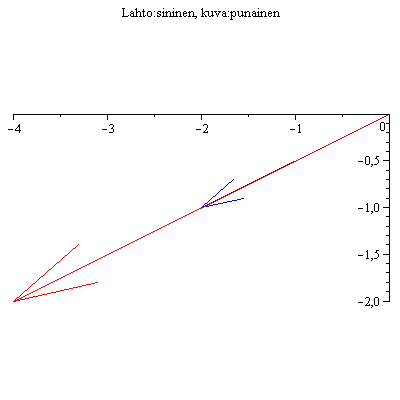
No kävipä ihmeellinen sattuman oikku! Lähtö ja kuva osuivat samalle suoralle!!
Jos näin ihmeellisesti käy, sanotaan, että kyseessä on A:n ominaisvektori. Kuvan mukaan näyttäisi siltä, että punainen nuoli on n. 2 kertaa sinisen
pituinen. Siinä tapauksessa sanotaan, että vastaava ominaisarvo = 2 .
Miten hakisimme yleisemmin? Otetaan (sinisiä) yksikkövektoreita sopivan tiheästi ja kuvataan A:lla. Toisin sanoen jaetaan yksikköympyrän kehä
tasavälisesti riittävän hienolla jaolla.
Tässä koodi, jonka kokosimme yllä funktioksi nuoletAni
| > |
#n:=80:display(seq(kuvakulma(A,<cos(Theta),sin(Theta)>),Theta=[seq(k*2*Pi/n,k=0..n)]),insequence=true,scaling=constrained);
|
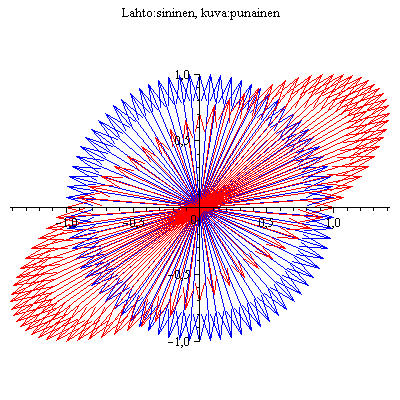
| > |
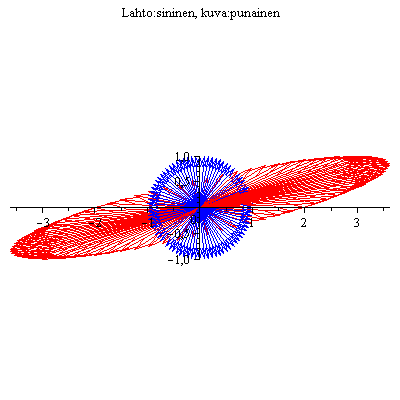
nuoletAni(A,80); # Klikkaa kuvaa => saat animaatiovalikon. Aja kehys kerrallaan tai jatkuvasti. Valikon saat kuvasta myös hiiren oikeaa painamalla, mutta edellinen on helpompi ja monipuolisempi. Tässa on ehkä opettavaisinta k"yttaa liukuluikuria. |
Tässä näkyy kummankin nuolen rata, mutta ei se, mikä sininen kuvautuu millekin punaiselle. Siispä ominaisvektorit eivät tästä staattisesta kuvasta paljastu. (Mutta esteettistä mielihyvää se voi tuottaa, ja sitäpaitsi ehkä selventää edellisen funktion toimintaperiaatetta ja n"yttää vektorien ratakäyrat.)
Esim 2.
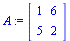 |
(4.4) |
| > |
nuoletAni(A,80); #Klikkaa animaatiovalikko. |
| > |
#piirraM(A.talo); piirraM(A.ympyra); |
Nuolet pyörivät nyt vastakkaisiin suuntiin, Toinen ominaissuunta on siinä, missä vektorit ovat päällekkäin, toinen siinä, missä ne ovat vastakkaissuuntaiset.
No lasketaan:
| > |
karpoly:=Determinant(A-lambda*Id(2));Lambda:=solve(karpoly=0,lambda); |
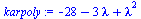 |
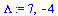 |
(4.5) |
| > |
Eigenvectors(A); # Katsotaan valmiilla funktiolla. |
, Matrix(%id = 418363688)](images/ominaisarvot_53.gif) |
(4.6) |
Ominaisvektoria [1,1] matriisi A venyttää kertoimella 7 ja vektoria [-6,5] kertoimella 4, miinus-merkki tarkoittaa, että vektorit ovat vastakkaissuuntaiset.
Tarkistetaan vielä
](images/ominaisarvot_54.gif) |
](images/ominaisarvot_55.gif) |
(4.7) |
 = Vector[column](%id = 419197880)](images/ominaisarvot_56.gif) |
 = Vector[column](%id = 418838308)](images/ominaisarvot_57.gif) |
(4.8) |
Niinpä on!
| > |
N:=50: h:=2*Pi/N:t:=seq(k*h, k=1..N+1):x:=map(cos,[t]): y:=map(sin,[t]): |
| > |
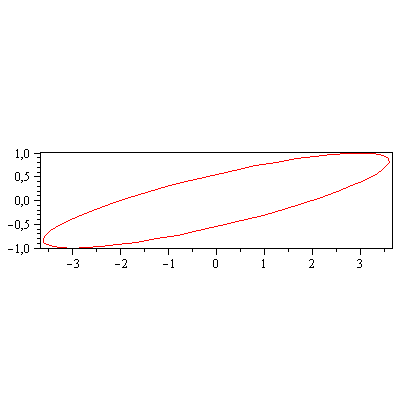
display(piirraM(A.ympyra),piirraMb(ympyra),arrow([7*v1/Norm(v1,2),4*v2/Norm(v2,2)],scaling=constrained,shape=arrow)); |
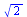 |
(4.9) |
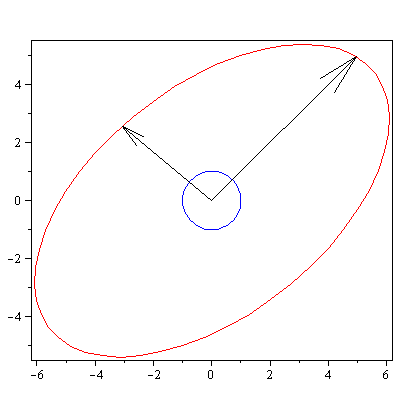
Sininen yksikköympyrä, punainen kuvaellipsi, yksikköominaisvektorien kärjet ovat nuolien ja sinisen ympyrän leikkauspisteissä, ominaisarvoilla kerrottuna ne
yltävät ellipsin kehälle puoliakselien kohdalla.
Esim 3 Onko kiertokuvauksella ominaisarvoja/vektoreita?
| > |
A:=<<cos(phi),sin(phi)>|<-sin(phi),cos(phi)>>; |
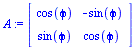 |
(4.10) |
| > |
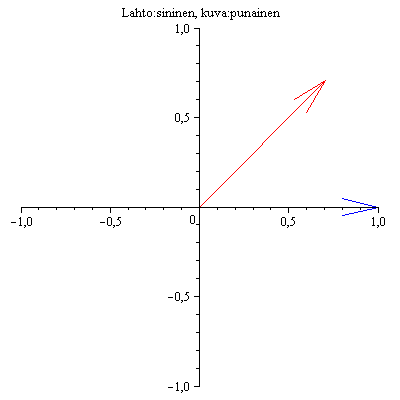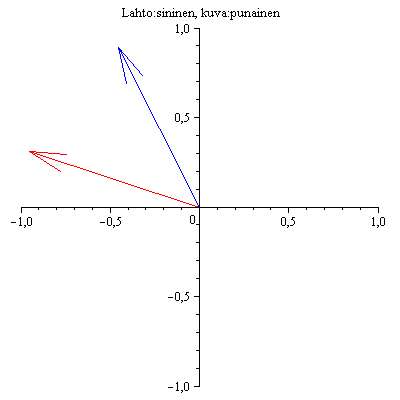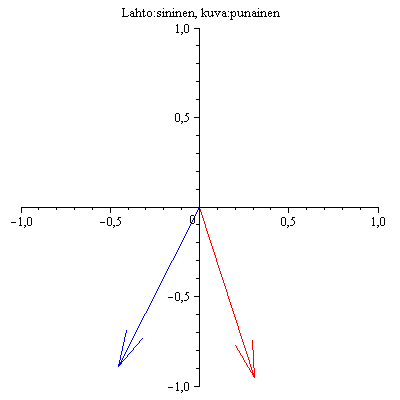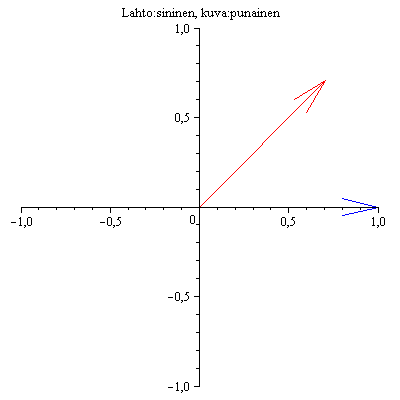
phi:=Pi/4:nuoletAni(A,40); # Animaatio, klikkaa kuvaa. |
No ei sitten millään voi olla ominaisarvoja, nuolet pyörivät samaa vauhtia, eivätkä missään mene päällekkäin.
Mutta mutta ... mehän sallimme myös kompleksiset skalaarit. Kompleksikertlaskuhan on tason kiertoa!
Lasketaanpa!
| > |
karpoly:=Determinant(A-lambda*Id(2));
|
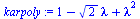 |
(4.11) |
| > |
lam:=solve(karpoly=0,lambda);
|
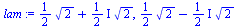 |
(4.12) |
| > |
M1:=A-lam[1]*Id(2);rM1:=ref(M1);
|
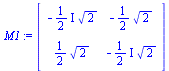 |
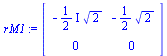 |
(4.13) |
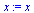 |
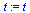 |
(4.14) |
| > |
x2:=t: x1:=solve(rM1[1,1]*x+rM1[1,2]*x2=0,x);
|
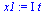 |
(4.15) |
](images/ominaisarvot_69.gif) |
(4.16) |
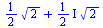 |
(4.17) |
](images/ominaisarvot_71.gif) |
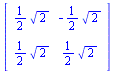 |
(4.18) |
| > |
A.v,map(evalc,lam[1].v); |
, Vector[column](%id = 419417204)](images/ominaisarvot_73.gif) |
(4.19) |
Samoja ovat, joten oikein laskettiin. Toinen ominaisarvo/vektori saadaan kompleksikonjugoimalla.
Kysymys: Onko nyt niin, että joko nuolet menevät jossain päällekkäin (reaaliset ominaisarvot) tai kyseessä on kierto.
Vastaus: Kyllä, paitsi kiertoon voi yhdistyä venytys/kutistus (kertominen reaalisella skalaarilla).
Onko tässä siis kaikki, mitä 2 x 2-matriisesita voidaan yleisesti sanoa? Eipä olekaan!
Kukaan ei ole sanonut, että ominaisvektoreita on aina kaksi lineaarisesti riippumatonta. No onko vai ei?
| > |
A1:=<<1,0>|<1,1>>; #A2:=<<1,1>|<-1,-1>>; A3:=<<0,0>|<1,0>>; |
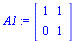 |
(4.20) |
| > |
karpoly1:=det(A1-lambda*Id(2));#karpoly2:=det(A2-lambda*Id(2));karpoly3:=det(A3-lambda*Id(2)); |
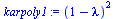 |
(4.21) |
![[1, 2, {array( 1 .. 2, [( 1 ) = 1, ( 2 ) = 0 ] )}]](images/ominaisarvot_76.gif) |
(4.22) |
Tämä tarkoittaa, että A1:n ominaisrvo 1 on kaksinkertainen (senhän jo näimme edellä), ja sillä on vain yksi LRT ominaisvektori [1,0]. Tutkitaanpa:
Huomataan, että nuolet menevät kaksi kertaa samalle suoralle, mutta kyseessä on sama x-akseli kummallakin kertaa. Sillä perusteella on vain yksi LRT ominaisvektori. Tässä tapauksessa mistään kompleksikosmoksesta ei voi tipahtaa ylimääräisiä ominaisvektoreita, sillä kompleksitapauksessa kaksinkertainen ominaisarvo ei ole mahdollinen. (Miksi?)
| > |
piirraM(A1.ympyra); # Vertaa tätä edelliseen animaatioon, niin ymmärrät. Nyt ei max venymä/kutistuma edustakaan ominaisarvoa. |
Kysymys: Ovatko ellipsin puoliakselivektorit hyödyllisiä, miten ne liittyvät yleisiin lineaarialgebrakäsitteisiin?
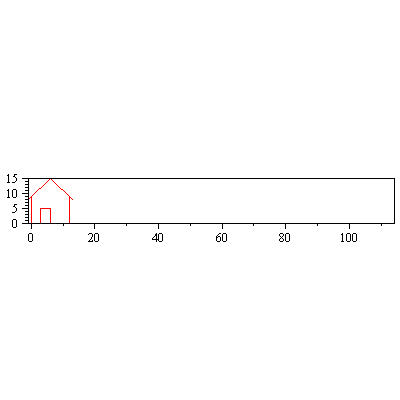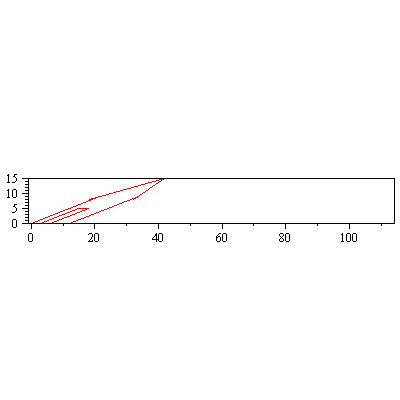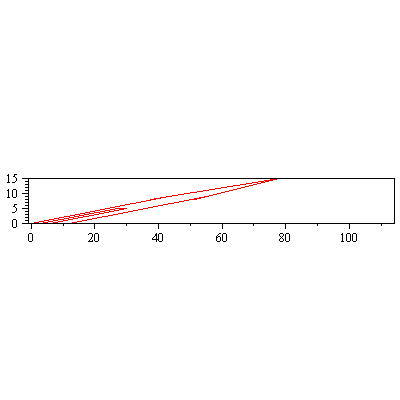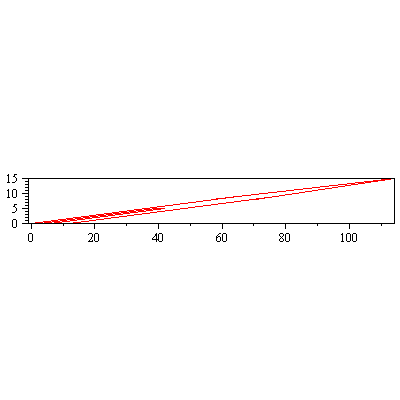
, Matrix(%id = 418363688)](images/ominaisarvot_53.gif)
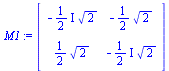
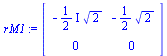
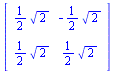
, Vector[column](%id = 419417204)](images/ominaisarvot_73.gif)