Fourier-sarjojen perustyöarkki
17.11.00 HA
Apufunktioita: JJ, trigsiev, jana
>
restart:with(plots):
Warning, the name changecoords has been redefined
> #read("/p/edu/mat-1.414/maple/ohjelmat.mpl"):
> #read("c:\\opetus\\maple\\ohjelmat.mpl"):
> read("/home/apiola/opetus/peruskurssi/v2-3/maple/ohjelmat.mpl"):
Määritellään uudet koodit varmuuden vuoksi myös tässä, vaikka ovatkin ohjelmat.mpl:ssä.
>
trigsiev:=proc(lauseke,n)
local tulos;
tulos:=subs(sin(n*Pi)=0,lauseke);
tulos:=subs(cos(n*Pi)=(-1)^n,tulos);
tulos:=subs((-1)^(2*n)=1,tulos);
simplify(tulos);
end:
> jana:=(x,y)->plot([[x,0],[x,y]],thickness=3,color=blue):
> #display([seq(jana(n,abs(an)),n=1..6)],axes=box);
Fourier-kertoimet
Reaalinen muoto, cos ja sin
Nämä on syytä ottaa pohjaksi työskentelyyn ja olla valmis modifioimaan esim. integrointirajoja,
integrointia paloittain ym. (Kokemus opettaa välttämään liian pitkälle vietyä automatiikkaa.)
> f:='f': T:='T': omega:='omega': #omega:=2*Pi/T:
>
a0:=(2/T)*int(f(t),t=0..T):
an:=(2/T)*int(f(t)*cos(n*omega*t),t=0..T):
bn:=(2/T)*int(f(t)*sin(n*omega*t),t=0..T):
> sarja:=a0/2+sum(an*cos(n*omega*t)+bn*sin(n*omega*t),n=1..infinity):
> osasumma:=N->a0/2+sum(an*cos(n*omega*t)+bn*sin(n*omega*t),n=1..N):
>
Sinisarja ja kosinisarja
Jäljempänä esitämme parillisen ja parittoman laajennusoperaattorin. Käytännössä parillista/paritonta laajennusta vastaa kosini/sinisarja, jossa lähdetään liikkeelle välillä [0,d] määritellystä funktiosta f, joka laajennetaan parilliseksi/parittomaksi. Tällöin yllä olevat kaavat tulevat muotoon:
1) kosinisarja:
> f:='f': T:='T': omega:='omega': #omega:=2*Pi/T:
> a0:=(1/d)*int(f(t),t=-d..d);an:=(1/d)*int(f(t)*cos(n*omega*t),t=-d..d);bn:=0;
>
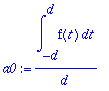
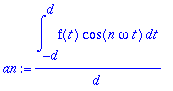
![]()
Koska yllä olevat integroitavat ovat parilllisia, voidaan integroida [0..d], kunhan tulos kerrotaan 2:lla.
Tällöin tullaan toimeen alkuperäisellä, välillä [0,d] määritellyllä funktiolla, eikä tarvitse kohdistaa integrointia parilliseen laajennukseen. Siispä kosinisarjakaavat ovat:
>
f:='f':T:='T':omega:='omega':#omega:=2*Pi/T:
a0:=(2/d)*int(f(t),t=0..d);
an:=(2/d)*int(f(t)*cos(n*omega*t),t=0..d);bn:=0;
sarja:='a0'/2+sum('an'*cos(n*omega*t),n=1..infinity);
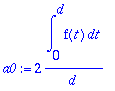
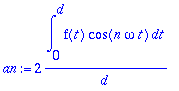
![]()
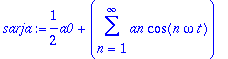
Sinisarja saadaan aivan vastaavasti:
>
f:='f':T:='T':omega:='omega':#omega:=2*Pi/T:
bn:=(2/d)*int(f(t)*sin(n*omega*t),t=0..d);
sarja:=sum('bn'*cos(n*omega*t),n=1..infinity);
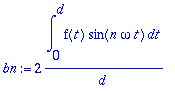
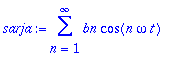
Kompleksinen muoto
Kokeillaan vaihteeksi sellaista tyyliä, että c on n:n funktio, tässä se on mukavaa, kun kaavatkin ovat yhtenäiset. c-funktio on syytä määritellä unapply-tavalla. Laskentatehossa nimittäin on dramaattinen ero. (unapply evaluoi (esim. integroi) määrittelyaikana, kun taas -> määrittely tekee sen kutsuaikana.)
> T:='T': f:='f': omega:='omega': omega:=2*Pi/T:
> c:=unapply(1/T*int(f(t)*exp(-I*n*omega*t),t=0..T),n);c(0):=1/T*int(f(t),t=0..T);
Vaikka seuraava toimii, niin ei kannata tehdä, kts. yllä.
> #c:=n->1/T*int(f(t)*exp(-I*n*omega*t),t=0..T);
> sarja:=sum('c(n)'*exp(I*n*'omega'*t),n=-infinity..infinity);
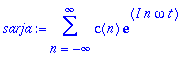
Esim.
Muodosta alla määriteltävän funktion Fourier-sarja, piirrä jaksollinen laajennus ja Fourier-osasummien kuvaajia. Piirrä myös taajuusspektrit. Käsittele sekä reaalimuotoista sin/cos-sarjaa että kompleksimuotoista.
> f:=t->piecewise(-Pi<t and t < 0,t+Pi,0<t and t<Pi,Pi);
![]()
> plot(f,-Pi..Pi);
![[Maple Plot]](images/fourier12.gif)
> jaksf:=JJ(f,-Pi..Pi):
> plot(jaksf,-2*Pi..2*Pi);
![[Maple Plot]](images/fourier13.gif)
> T:=2*Pi:omega:=2*Pi/T:
>
a0:=(2/T)*int(f(t),t=-Pi..Pi);
an:=(2/T)*int(f(t)*cos(n*omega*t),t=-Pi..Pi):an:=trigsiev(an,n);
bn:=(2/T)*int(f(t)*sin(n*omega*t),t=-Pi..Pi):bn:=trigsiev(bn,n);
![]()
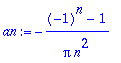
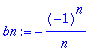
Koska halusimme välttyä assume -komennon aiheuttamilta sivuvaikutuksilta, sievensimme omalla trigsiev- komennolla. Huomaamme, että int osasi käsitellä piecewise -määriteltyä funktiota ihan nätisti. Luultavaa on, että se osaa myös epäjatkuvalle, mutta kannattaa tarkkailla.
> sarja:=a0/2+sum(an*cos(n*omega*t)+bn*sin(n*omega*t),n=1..infinity);
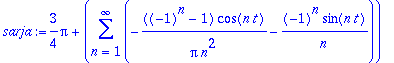
> osasumma:=N->a0/2+sum(an*cos(n*omega*t)+bn*sin(n*omega*t),n=1..N);
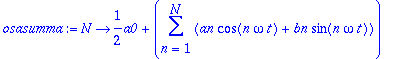
> osasumma(5);
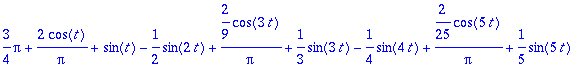
Tässä tyylissä (jossa an ja bn integroitiin symbolisesti valmiiksi), on aivan sopivaa (ja suositeltavaa) käyttää -> funktiomääritystapaa.
> plot([jaksf(t),osasumma(10)],t=-2*Pi..2*Pi);
![[Maple Plot]](images/fourier20.gif)
> plot([jaksf(t),seq(osasumma(k),k=1..10)],t=-2*Pi..2*Pi);
![[Maple Plot]](images/fourier21.gif)
Taajuusspekrit:
Piirtäminen hoituu oikein näppärästi yllä määrittelemällämme jana -funktiolla.
> A0:=a0/2; An:=abs(an-I*bn);
![]()
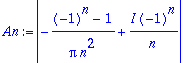
> phi0:=0: phin:=argument(an-I*bn);
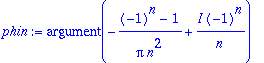
> display([jana(0,A0),seq(jana(n,An),n=1..6)],axes=box,title="Amplitudispektri");display([jana(0,phi0),seq(jana(n,phin),n=1..6)],title="Vaihespektri");
![[Maple Plot]](images/fourier25.gif)
![[Maple Plot]](images/fourier26.gif)
Kompleksinen muoto
> c:=unapply(1/T*int(f(t)*exp(-I*n*omega*t),t=0..T),n);c(0):=1/T*int(f(t),t=0..T);
> sarja:=sum('c(n)'*exp(I*n*'omega'*t),n=-infinity..infinity);
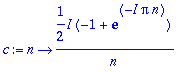
![]()
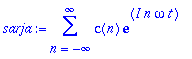
> c(0);
![]()
> c(1);
![]()
> seq(c(n),n=-5..5);
![]()
> display([seq(jana(n,abs(c(n))),n=-6..6)],axes=box,title="Amplitudispektri");
![[Maple Plot]](images/fourier33.gif)
> display([seq(jana(n,argument(c(n))),n=-6..6)],title="Vaihespektri");
![[Maple Plot]](images/fourier34.gif)
>
Parilliset ja parittomat laajennukset
Määritellään laajennusoperaattorit "
parillinenjatko"
ja "
paritonjatko
", jotka jatkavat
positiivisella R-akselilla määritellyn funktion parillisena/parittomana koko R:ään.
(Ovat ohjelmat.mpl:ssä)
> parillinenjatko:=f->unapply(piecewise(x>0,f(x),x<0,f(-x)),x):
> paritonjatko:=f->unapply(piecewise(x>0,f(x),x<0,-f(-x)),x):
> f:=t->t;
![]()
> plot(parillinenjatko(f),-1..1);
![[Maple Plot]](images/fourier36.gif)
> plot(paritonjatko(f),-1..1);
![[Maple Plot]](images/fourier37.gif)
> plot(paritonjatko(x->x^2),-1..1);
![[Maple Plot]](images/fourier38.gif)
> jakspariton:=JJ(paritonjatko(x->x^2),-1..1):
> plot(jakspariton,-3..3);
![[Maple Plot]](images/fourier39.gif)
Onpas meillä nyt hyvät välineet. Tehtävien ratkominen on pelkkää nautiskelua!
Lisäksi kannattaa ottaa vielä numeerisen integroinnin tapaus, mutta odotetaan vähän aikaa ...
Fourier-sarjan laskeminen numeerisesti integroiden
Titenkään integrointi ei aina onnistu symbolisesti. Otetaan esimerkki, jossa samalla tulee sinisarjan kaavan käyttö.
Kehitettävä sinisarjaksi välillä [-1,1] funktio:
> f:=t->t^sin(4*Pi*t);
![]()
> plot(paritonjatko(f),-1..1);
![[Maple Plot]](images/fourier41.gif)
> d:=1:omega:=Pi:
> b:=array(1..20):
>
for 'n' from 1 to 20 do
b['n']:=(2/d)*evalf(Int(f(t)*sin(n*omega*t),t=0..d));
od: n:='n':
Tässä yksi sitkeä Maple "feature" : for-loopin jälkeen n:llä on arvo 21, mikä johtaa jatkossa virhetilanteeseen, siksi n vapautetaan tässä.
> osasumma:=N->sum(b[n]*sin(n*omega*t),n=1..N);
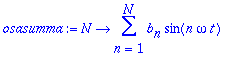
> osasumma(10);
![]()
![]()
> plot([paritonjatko(f)(t),op(map(osasumma,[3,5,7,17]))],t=-1..1);
![[Maple Plot]](images/fourier45.gif)
Tehtiin pikku briljeeraus vielä mappaamalla osasumma erinäisille indekseille.