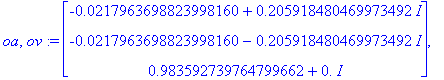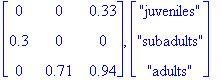Alustukset
| > | restart: |
| > | with(linalg): with(LinearAlgebra): |
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
| > | alias(rref=ReducedRowEchelonForm): alias(ref=GaussianElimination): alias(Diag=DiagonalMatrix,Id=IdentityMatrix): |
| > | with(plots): |
Warning, the name changecoords has been redefined
| > | #plotdots:=data->display([plot(data,style=point,symbol=circle,symbolsize=17,symbol=circle),plot(data,color=blue)]); |
| > | plotdots:=data->display([plot(data,style=point),plot(data,color=blue)]); |
![]()
| > | # Esim: |
| > | #plotdots([[0,0],[1,1],[1,0],[3,2]]); |
| > | traje:=proc(A,x0,n) local x,k; x[0]:=x0: for k to n do x[k]:=A.x[k-1]: end do: plotdots(map(convert,[seq(x[k],k=0..n)],list)); end: |
| > | trajedot:=proc(A,x0,n) local x,k; x[0]:=x0: for k to n do x[k]:=A.x[k-1]: end do: plot(map(convert,[seq(x[k],k=0..n)],list),style=point); end: |
| > | #traje(A,<-3,3>,10); |
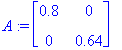
![v[1] := Vector(%id = 12966956)](images/L9maple6.gif)
![v[2] := Vector(%id = 12965876)](images/L9maple7.gif)
![x[k] := c[1]*.8^k*Vector(%id = 12966956)+c[2]*.64^k*Vector(%id = 12965876)](images/L9maple9.gif)
![xnollat1 := [Vector(%id = 13097332), Vector(%id = 12176892), Vector(%id = 20232872), Vector(%id = 14805280), Vector(%id = 13781032), Vector(%id = 13097112), Vector(%id = 13096952)]](images/L9maple12.gif)
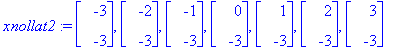
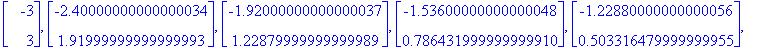
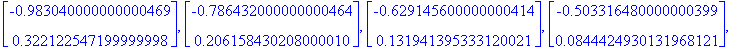
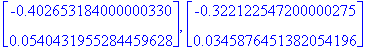
![[Maple Plot]](images/L9maple22.gif)
![jono[1] := [Vector(%id = 13097332)], [Vector(%id = 13624120)], [Vector(%id = 19357872)], [Vector(%id = 4301904)], [Vector(%id = 4369832)], [Vector(%id = 4438356)]](images/L9maple23.gif)
![jono[1] := [Vector(%id = 13097332)], [Vector(%id = 13624120)], [Vector(%id = 19357872)], [Vector(%id = 4301904)], [Vector(%id = 4369832)], [Vector(%id = 4438356)]](images/L9maple24.gif)
![[Maple Plot]](images/L9maple25.gif)
![[Vector(%id = 13097332), Vector(%id = 12176892), Vector(%id = 20232872), Vector(%id = 14805280), Vector(%id = 13781032), Vector(%id = 13097112), Vector(%id = 13096952)]](images/L9maple26.gif)
![[Maple Plot]](images/L9maple27.gif)
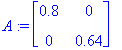
![x[11] := c[1]*Vector(%id = 5205500)+c[2]*Vector(%id = 5186920)](images/L9maple34.gif)
![[Maple Plot]](images/L9maple36.gif)
![[Maple Plot]](images/L9maple37.gif)
![[Maple Plot]](images/L9maple38.gif)
![[Maple Plot]](images/L9maple39.gif)
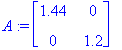
![[Maple Plot]](images/L9maple41.gif)
![[Maple Plot]](images/L9maple42.gif)
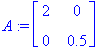
![[Maple Plot]](images/L9maple44.gif)
![[Maple Plot]](images/L9maple45.gif)
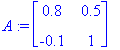
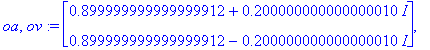
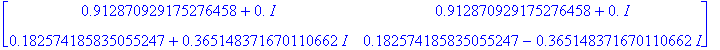
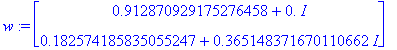
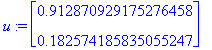
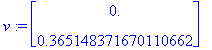
![[Maple Plot]](images/L9maple60.gif)
![[Maple Plot]](images/L9maple61.gif)

![x[k] = Vector(%id = 15078180)](images/L9maple65.gif)