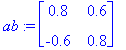Diagonalisoituvuus
Teoriaa
Muistathan aina , vaikka unissasi (ja jo 1. välikokeessa), ja osaathan todistaakin: Eri ominaisarvoihin liittyvät ominaisvektorit ovat LRT.
Määr: Neliömatriisit A ja B ovat similaariset , jos on olemassa säännöllinen (eli kääntyvä) matriisi S siten, että
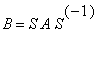 .
.
Jos A on
similaarinen diagonaalimatriisin kanssa
(ts. on olemassa diagonaalimatriisi D se.
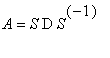 ), sanotaan, että A on
diagonalisoituva
), sanotaan, että A on
diagonalisoituva
(lyh. diagva).
Lause TE 4.5. s. 44, Lay Thm 5 " The Diagonalization Thm , s. 320, KRE Thm 5 s. 394 (asiallisesti sama, muotoilu hiukan vähemmän yleinen)
A (n x n ) on diagva, joss (jos ja vain jos)
A:lla on n kpl. LRT ominaisvektoreita, ts. A:n ominaisvektoreista voidaan muodostaa
![]() :n kanta, missä
:n kanta, missä
![]() tai
tai
![]() .
.
Erityisesti, jos A:n ominaisarvot ovat erilliset, niin A on diagva.
Seuraus 4.6
. A on diagva joss
![]() kaikilla ominaisarvoilla lambda . (Jokaisen ominaisarvon algebrallinen ja geometrinen kertaluku
kaikilla ominaisarvoilla lambda . (Jokaisen ominaisarvon algebrallinen ja geometrinen kertaluku
on sama.)
Palautetaan mieleen V2-asia , jota hyödynnettiin (ilman todistusta):
Symmetrinen matriisi on diagonalisoituva ja ominaisarvot ovat reaaliset .
Palaamme tämänkaltaisiin kysmyksiin, kunhan ensin
puhumme vähän sisätuloista ja ortogonaalisuudesta,
Diagonalisointiresepti : (seuraa suoraan päälauseen todistuksesta)
1) Lasketaan A:n ominaisarvot ja -vektorit (pessimistit laskevat vain geometriset kertaluvut).
Jos ominaisvektoreita ei ole tarpeksi, A ei diagonalisoidu.
2) Jos ominaisvektoreita on tarpeeksi, muodostetaan matriisit S ja
![]() , missä
, missä
- S:n sarakkeet ovat A:n ominaisvektorit.
-
![]() on diagonaalimatriisi, jossa diagonaalilla on ominaisarvot samassa järjestyksessä kuin S:ssä ominaisvektorit
on diagonaalimatriisi, jossa diagonaalilla on ominaisarvot samassa järjestyksessä kuin S:ssä ominaisvektorit
(eli ominaisarvot ja -vektorit vastaavat toisiaan).
3) Koska S:n sarakkeet LRT, voidaan muodostaa, ja siis muodostetaan
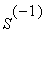 .
.
Tarkistus
: Kerrotaan
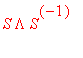 ja katsotaan, onko A.
ja katsotaan, onko A.
Diagonalisoinnin tarkoitus
on löytää matriisit
![]() ,
,
![]() ,
,
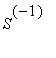 ja hyödyntää niitä esim. matriisin potenssien laskemisessa tms. analyysissa,
ja hyödyntää niitä esim. matriisin potenssien laskemisessa tms. analyysissa,
ei siis vain laskea ja todeta, että eräs matriisikaava on tosi.
Esim 1
Diagonalisoi seuraava matsriisi, jos mahdollista.
| > | A:=<<1,-3,3>|<3,-5,3>|<3,-3,1>>; |
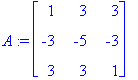
Koska ominaisarvojen ja -vektoreiden laskentaa on jo harjoiteltu, käytämme valmista Eigenvectors -funktiota.
| > |
| > |
Warning, premature end of input
| > | (oa,ov):=Eigenvectors(A); |
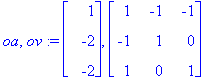
Valitettavasti tässä jää aika vähän tehtävää, koska Maple palauttaa mukavasti ov-matrisiin juuri siten, että sarakkeina ovat oa-vektorin alkoita
vastaavat ominaisvektorit. Jos ominaisvektoreita ei ole tarpeeksi, Maple palauttaa nollasarakkeen.
Normaalisti siis on määritettävä kunkin ominaisavaruuden kanta.
| > | S:=ov;Lambda:=Diag(oa); SI:=S^(-1); |
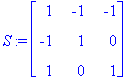
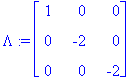
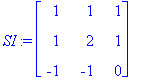
Tässä on siis matriisin diagonalisointi.
Voidaan tarkistaa:
| > | A = S.Lambda.SI; |
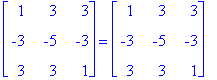
Lisää esimerkkejä, esim. KRE ss. 394 - 395
Katsotaan tässäkin lisää tapauksia.
Esim 2
Diagonalisoi, jos mahdollista:
| > | A:=<<2,-4,3>|<4,-6,3>|<3,-3,1>>; |
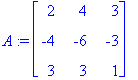
| > | Eigenvectors(A); |
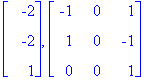
Nollasarake keskellä kertoo, että ominaisavaruudessa
![]() on vain yksi kantavektori, eli
on vain yksi kantavektori, eli
![]() , vaikka
, vaikka
![]()
Esim. 3
Diagonalisoi, jos mahdollista:
| > | A:=<<5,0,1,-1>|<0,5,4,-2>|<0,0,-3,0>|<0,0,0,-3>>; |
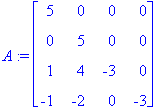
Koska kyseessä on kolmiomatriisi, ominaisarvot paistavat suoraan päälävistäjältä. Ovatko molemmat ominaisavaruudet 2-ulotteisia?
Turvaudumme halpamaiseen keinoon:
| > | (oa,ov):=Eigenvectors(A); |
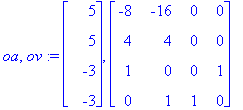
| > | S:=ov: Lambda:=Diag(oa): SI:=S^(-1): |
| > | diagonalisointi:=[S,Lambda,SI]; |
![diagonalisointi := [Matrix(%id = 5211528), Matrix(%id = 15486632), Matrix(%id = 4444156)]](images/L8maple27.gif)
| > | A,S.Lambda.SI; # Verrataan. |
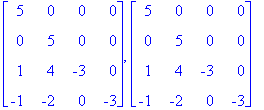
| > |
Kaupunkidynamiikkaa diagonalisoimalla
Vrt. myös TE Esim. 4.6, s. 46-47, KRE s. 377 Exa 2
| > | A:=<<.95,.05>|<.03,.97>>; A:=convert(A,rational); |
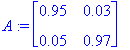
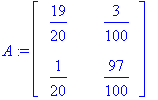
| > | (oa,ov):=Eigenvectors(A); |
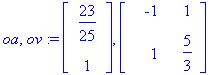
Jätetään normeeraamatta, koska ajosta toiseen muuttuminen osoittautui hankalaksi.
| > | # ov[1..-1,2]:=3*ov[1..-1,2]: ov; # Ei mitenkään välttämätöntä. # Huomaa, että Maple saattaa vaihdella järjestystä, joten voit # joutua vaihtamaan sarakenumeroa. # Huom2: Ominaisarvojen muodostamaa vektoria ei missään nimessä saa normeerata! |
| > | S:=ov: SI:=S^(-1): Lambda:=Diag(oa): |
| > | S,Lambda,SI; |
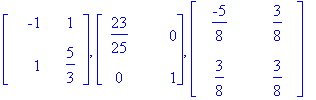
| > | Lambda_pot_k:=map(x->x^k,Lambda); |
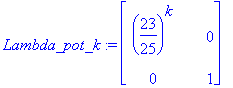
| > | Lambda_limes:=map(limit,Lambda_pot_k,k=infinity); |
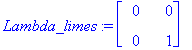
| > | lim_A_potenssiin_k:=S.Lambda_limes.SI; |
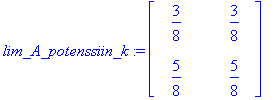
| > | alias(Alim=lim_A_potenssiin_k): |
| > | Alim.<1,0>, Alim.<0,1>; |
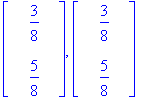
| > | Alim.<p,1-p>; |
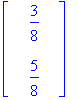
Sama tulos, olipa alkupiste mikä tahansa todennäköisyysvektori (tai ylimalkaan vektori, jonka koordinaattisumma = 1)..
Ominaisvektorikantalasku
L7maple
-työarkilla osoitti, että tulos on ominaisvektorin
![]() suuntainen tod. vektori, eli juuri yllä oleva.
suuntainen tod. vektori, eli juuri yllä oleva.
(Laskut ovat hyvin läheistä sukua toisilleen.)
Käytetään lopuksi raakaa voimaa ja verrataan:
| > | A:=convert(A,float); # seq(A^k,k=1..10); |
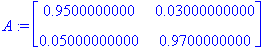
| > | A20:=(A^20); |
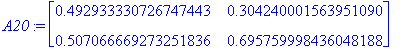
| > | A40:=A20.A20; |
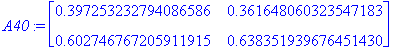
| > | A80:=A40.A40; |
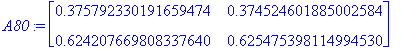
| > | A160:=A80.A80; |
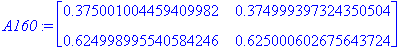
| > | convert(Alim,float); |
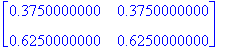
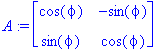
![[Maple Plot]](images/L8maple46.gif)
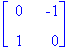
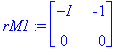
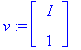
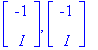
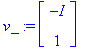
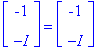
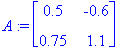
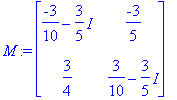
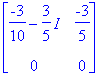
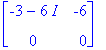
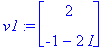
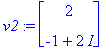
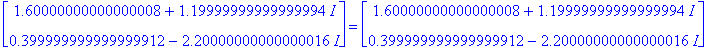
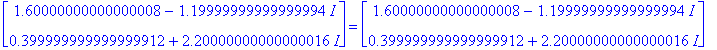
![[Maple Plot]](images/L8maple68.gif)
![[Maple Plot]](images/L8maple69.gif)