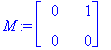../L/L7maple.mws
L 12 to 3.10.02
Alustukset
| > |
with(LinearAlgebra):
with(linalg):
|
| > |
with(plots):setoptions(scaling=constrained):setoptions3d(axes=boxed,orientation=[-30,50]):
|
| > |
alias(Inv=MatrixInverse,Id=IdentityMatrix,Diag=DiagonalMatrix):
|
| > |
alias(rref=ReducedRowEchelonForm):alias(ref=GaussianElimination):
alias(Id=IdentityMatrix):
|
Lineaarikuvaukset tasossa ja niiden havannollistaminen
Maple 8:n funktio
plots[arrow]
on maanmainio! Tehdään sitä käyttävä apufunktio, jolla piirretään sininen nuoli origosta vektorin u määräämään pisteeseen ja punainen nuoli O:sta kuvapisteeseen Au.
| > |
kuvakulma:=(A,u)->display(arrow(u,shape=arrow,color=blue),arrow(A.u,shape=arrow,color=red),scaling=constrained,title="Lahto:sininen, kuva:punainen");
|
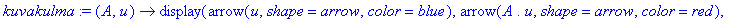
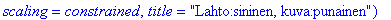
Esim
. 1
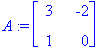
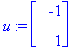
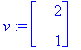
| > |
kuvakulma(A,u);kuvakulma(A,v);
|
![[Maple Plot]](images/L7maple6.gif)
![[Maple Plot]](images/L7maple7.gif)
Toisella yrittämällä osuimme ominaisvektoriin. Kuvan mukaan näyttäisi siltä, että vastaava ominaisarvo = 2.
Miten hakisimme yleisemmin? Otetaan (sinisiä) yksikkövektoreita sopivan tiheästi ja kuvataan A:lla.
| > |
display(seq(kuvakulma(A,<cos(Theta),sin(Theta)>),Theta=[seq(k*2*Pi/10,k=0..10)]));
|
![[Maple Plot]](images/L7maple8.gif)
| > |
n:=30:display(seq(kuvakulma(A,<cos(Theta),sin(Theta)>),Theta=[seq(k*2*Pi/n,k=0..n)]),insequence=true,scaling=constrained);
|
![[Maple Plot]](images/L7maple9.gif)
Löydetään toinenkin ominaisvektori aika läheltä. Koska sininen nuoli peittää punaisen, niin siinä ominaisarvo
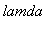 on välillä [0,1].
on välillä [0,1].
Toinen esimerkki:
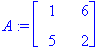
| > |
n:=40:display(seq(kuvakulma(A,<cos(Theta),sin(Theta)>),Theta=[seq(k*2*Pi/n,k=0..n)]),insequence=true,scaling=constrained);
|
![[Maple Plot]](images/L7maple12.gif)
No lasketaan:
| > |
karpoly:=det(A-lambda*Id(2));
|
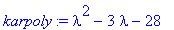
| > |
Lambda:=solve(karpoly=0,lambda);
|
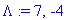
| > |
rref(A-Lambda[1]*Id(2));
|
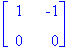
x2 on vapaa, x1=x2, joten esim. [1,1] kelpaa.
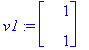
| > |
rref(A-Lambda[2]*Id(2));
|
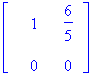
x2 vapaa, x1=-(6/5)x2, joten x2=5, x1=-6 kelpaa:
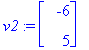
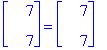
| > |
arrow([v1,v2],scaling=constrained);
|
![[Maple Plot]](images/L7maple20.gif)
Esim 2 Onko kiertokuvauksella ominaisarvoja/vektoreita?
| > |
A:=<<cos(phi),sin(phi)>|<-sin(phi),cos(phi)>>;
|
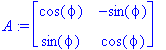
| > |
n:=40:display(seq(kuvakulma(A,<cos(Theta),sin(Theta)>),Theta=[seq(k*2*Pi/n,k=0..n)]),insequence=true,scaling=constrained);
|
![[Maple Plot]](images/L7maple22.gif)
No ei sitten millään voi olla ominaisarvoja, eihän? Vai voiko sittenkin?
Lasketaanpa!
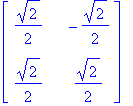
| > |
karpoly:=det(A-lambda*Id(2));
|
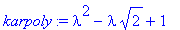
| > |
lam:=solve(karpoly=0,lambda);
|
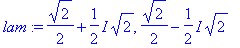
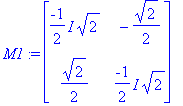
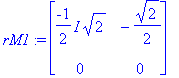
| > |
x2:=t: x1:=solve(rM1[1,1]*x+rM1[1,2]*x2=0,x);
|
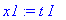
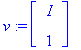
Tarkistetaan:
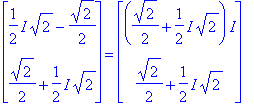
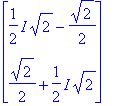
Yhtä hyvin:
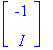
Kompleksiset vektorit voivat näyttää kovasti erilaisilta, vaikka ovat LRV.
| > |
rref(M1); # Huom! rref sekoaa, johtuuko kompleksiluvuista? Kysymys Maplesoftille!
|
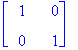
| > |
Eigenvectors(A);eigenvectors(A);
|
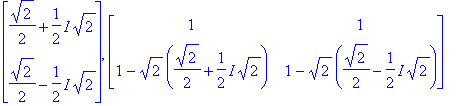
![[1/2*2^(1/2)+1/2*I*2^(1/2), 1, {vector([-1+2^(1/2)*(1/2*2^(1/2)+1/2*I*2^(1/2)), 1])}], [1/2*2^(1/2)-1/2*I*2^(1/2), 1, {vector([-1+2^(1/2)*(1/2*2^(1/2)-1/2*I*2^(1/2)), 1])}]](images/L7maple35.gif)
Ominaisarvojen laskentaa Maplella
| > |
with(LinearAlgebra):
with(linalg):
|
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
| > |
with(plots):setoptions(scaling=constrained):setoptions3d(axes=boxed,orientation=[-30,50]):
|
Warning, the name changecoords has been redefined
| > |
alias(Inv=MatrixInverse,Id=IdentityMatrix,Diag=DiagonalMatrix):
|
| > |
alias(rref=ReducedRowEchelonForm):alias(ref=GaussianElimination):
alias(Id=IdentityMatrix):
|
Käsinlaskutyyli vs. eigenvectors/Eigenvectors
| > |
A:=<<2,0,4> | <0,6,0> | <4,0,2>>;
|
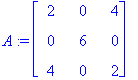
| > |
p:=det(A-lambda*Id(3));factor(p);# Karakteristinen polynomi
|
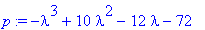
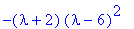
| > |
lam:=solve(%=0,lambda);
|
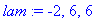
Ominaisarvon 6
algebrallinen kartaluku on 2.
| > |
M1:=A-lam[1]*Id(3);
M2:=A-lam[2]*Id(3);
|
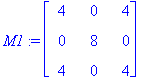
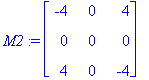
| > |
{lam[1],ref(M1)},{lam[2],ref(M2)};
|
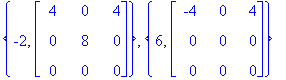
Ominaisavruuksien dimensiot nähdään suoraan tästä: 1 ja 2 (ei-pivot.-sarakkeiden lkm antaa nulliteetin, yhtä hyvin nollarivien lkm,
kun kerran neliömatr.)
Ominaisvektorien laskemista varten on mukavampaa muodostaa rref. (Kannattaa
kuitenkin verrata rref-tulosta ref-tulokseen. Jos ovat ristiriidassa, niin ref on luotettavampi,
sillä rref saattaa helpommin harhautua pyöristysvirheiden takia.) (rref saattaa ryhtyä käyttämään
pivottina alkiota, joka pitää tulkita nollaksi.)
| > |
{lam[1],ref(M1)},{lam[2],ref(M2)};
|
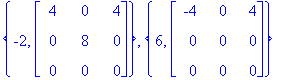
![lambda[1] = -2](images/L7maple44.gif)
| > |
v1:=subs(t=1,<x1,x2,x3>);
|
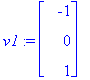
![lambda[2] = 6](images/L7maple46.gif)
| > |
v2:=subs(t=1,s=0,<x1,x2,x3>);v3:=subs(t=0,s=1,<x1,x2,x3>);
|
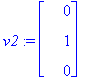
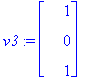
Ominaisarvoon
![lambda[2] = 6](images/L7maple49.gif) liittyy kaksi LRT ominaisvektoria, joten tämän ominaisarvon geometrinen kertaluku = 2. (Algebrallinen kertalukuhan on myös 2.)
liittyy kaksi LRT ominaisvektoria, joten tämän ominaisarvon geometrinen kertaluku = 2. (Algebrallinen kertalukuhan on myös 2.)
Katsotaan vielä valmiilla funktioilla:
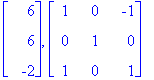
Ominaisarvosarake ja samassa järjestyksessä ominaisvektorisarakkeet.
| > |
(oa,ov):=Eigenvectors(A); # Kätevä tapa samanaikaisesti sijoittaa kahteen muuttujaan.
|
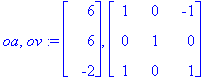
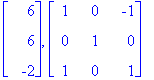
Katsotaan vanhalla linalg-tyylillä:
| > |
eigenvectors(A); # eigenvectors ei pane pahakseen, vaikka matriisirakenne on uudenaikainen.
|
![[6, 2, {vector([1, 0, 1]), vector([0, 1, 0])}], [-2, 1, {vector([-1, 0, 1])}]](images/L7maple53.gif)
[Ominaisarvo, alg. kertaluku,{ominaiskanta}], [Ominaisarvo, alg. kertaluku,{ominaiskanta}]
Tämä on havainnollinen katsoa, mutta hankalampi poimia.jatkokäsittelyyn.
Kannattaa kokeilla kumpaakin.
Esim. TE 4.5 s. 42
| > |
A:=<<5,-1,1> | <4,0,-2> | <3,-3,1>>;
|
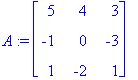
| > |
p:=det(A-lambda*Id(3));factor(p);# Karakteristinen polynomi
|
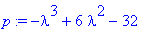
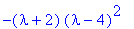
| > |
lam:=solve(%=0,lambda);
|
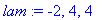
| > |
M1:=A-lam[1]*Id(3);
M2:=A-lam[2]*Id(3);
|
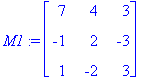
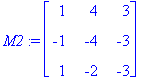
| > |
{lam[1],ref(M1)},{lam[2],ref(M2)};
|
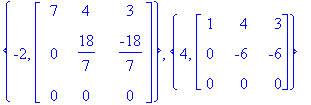
Ominaisarvon 4 alg, kertaluku = 2, mutta geom. kertaluku vain 1. Ominaisarvo on
defektiivinen
.
Ominaisvektoreista ei saada
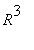 :n kantaa.
:n kantaa.
Esimerkki dynaamisesta systeemista, kaupunki/esikaupunki-analyysi
| > |
A:=<<.95,.05>|<.03,.97>>; A:=convert(A,rational);
|
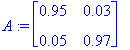
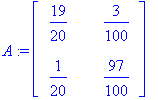
![x[k+1] = A*x[k]](images/L7maple64.gif) ,
,
![x[0] = [.6, .4]](images/L7maple65.gif)
| > |
p:=det(A-lambda*Id(2));factor(p);# Karakteristinen polynomi
|
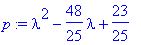
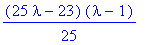
| > |
lam:=solve(%=0,lambda);
|
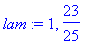
| > |
M1:=A-lam[1]*Id(2);
M2:=A-lam[2]*Id(2);
|
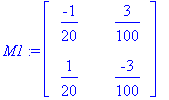
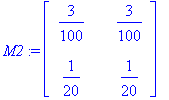
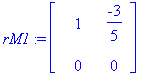
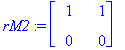
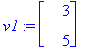
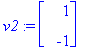
| > |
lam[2];convert(%,float);
|
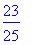
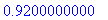
Esitetään alkupiste
![x[0]](images/L7maple77.gif) kannassa
kannassa
 .
.
| > |
#x0:=convert(<.6,.4>,rational):
|
| > |
c:=LinearSolve(<<v1>|<v2>>,x0);
|


Esim: Lausuttava annettu vektori matriisin
ominaisvektorikannassa
Edellä teimme tämän. Otetaan uudestaan erillisenä tehtävänä, tätä tarvitaan usein.
Itse asiassa kyse on aivan samasta kuin matriisin diagonalisoinnissa. Tässä tyylissä lasketaan vektorimuodossa.
| > |
A:=<<9/10,1/10>|<3/10,7/10>>;
|
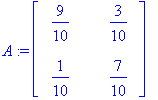
| > |
(oa,ov):=Eigenvectors(A);
|
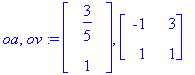
| > |
v1:=ov[1..-1,1];v2:=ov[1..-1,2];
|
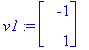
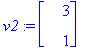
Tarkistetaan ominaisarvo/vektoriominaisuus:
| > |
A.v1 = oa[1]*v1;
A.v2 = oa[2]*v2;
|
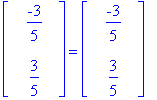
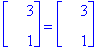
Ladotaan ominaisvektorit vierekkäin matriisiksi. Koska vektorit liittyvät eri ominaisarvoon, tiedämme jo suoraan, että ne ovat LRT. Siten niiden muodostama matriisi on kääntyvä.
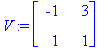
Olkoon u annettu mieleivaltainen vektori.
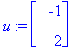
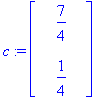
Tässä ovat vektorin u koordinaatit kannassa {v1,v2}.
Tarkistetaan vielä:
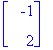
Kyllä vaan!
Lisää esimerkkejä defektiivisistä matriiseista
Kyse on matriiseista, joilla ei ole tarpeeksi ominaisvektoreita. Toisin sanoen jonkin ominaisarvon geometrinen kertaluku
on aidosti algebrallista pienempi:
| > |
 < M[a](lambda)](images/L7maple91.gif)
|
| > |
A1:=<<1,0>|<1,1>>; A2:=<<1,1>|<-1,-1>>; A3:=<<0,0>|<1,0>>;
|
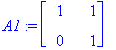
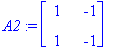
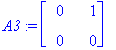
A3 on Strangin mukaan (s. 252) paras esimerkki testaamaan ominaisarvoväittämiä. Monissa tosi/epätosi-kysymyksissä tämä antaa vastauksen "epätosi".
| > |
map(eigenvectors,[A1,A2,A3]);
|
![[[1, 2, {vector([1, 0])}], [0, 2, {vector([1, 1])}], [0, 2, {vector([1, 0])}]]](images/L7maple95.gif)
Asia selvisi kerralla. Kaikissa kaksinkertainen ominaisarvo (A1:ssä 1, muissa 0). Jokaisessa vain 1-ulotteinen ominaisavaruus.
(Jopa kolmen eri matriisin voimin). Katsotaan vielä uutta tyyliä:
| > |
map(Eigenvectors,[A1,A2,A3]);
|
![[Vector(%id = 14422052), Matrix(%id = 12211076), Vector(%id = 14422132), Matrix(%id = 14560268), Vector(%id = 14422252), Matrix(%id = 13898300)]](images/L7maple96.gif)
Tämä tulos on hiukan hämmentävän näköinen. Ominaisvektorimatriisn nolla-sarakkeet täytyy tulkita tyhjiksi.
| > |
p:=det(A3-lambda*IdM(2));
|
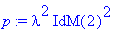
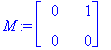
x2=0, x1=t, eli t*[1,0] on ominaisavaruus, kuten valmiit eigenvectors- ja Eigenvectors-funktiot jo laskivat.
![]()
![]()
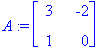
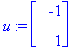
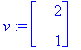
![[Maple Plot]](images/L7maple6.gif)
![[Maple Plot]](images/L7maple7.gif)
![[Maple Plot]](images/L7maple8.gif)
![[Maple Plot]](images/L7maple9.gif)
![]() on välillä [0,1].
on välillä [0,1].
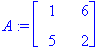
![[Maple Plot]](images/L7maple12.gif)
![]()
![]()
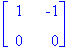
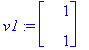
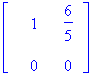
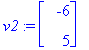
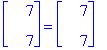
![[Maple Plot]](images/L7maple20.gif)
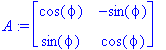
![[Maple Plot]](images/L7maple22.gif)
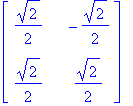
![]()
![]()
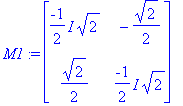
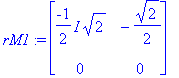
![]()
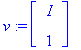
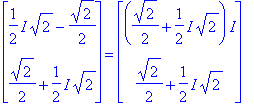
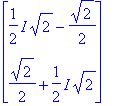
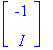
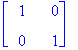
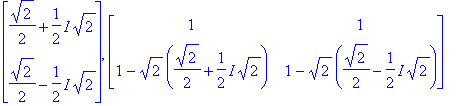
![]()
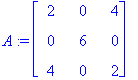
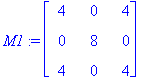
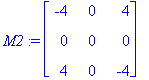
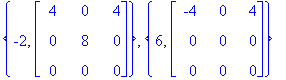
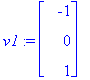
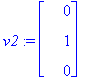
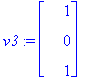
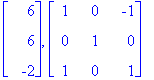
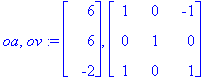
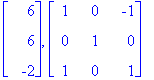
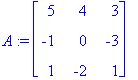
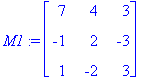
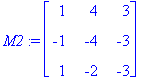
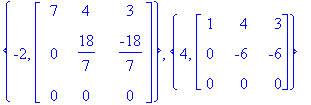
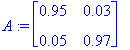
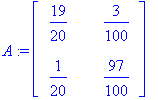
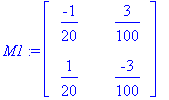
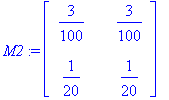
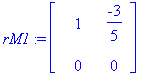
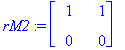
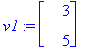
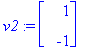


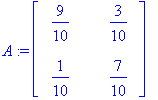
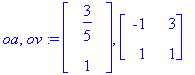
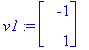
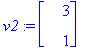
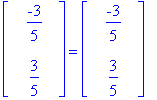
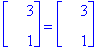
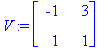
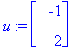
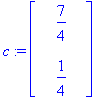
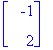
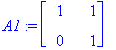
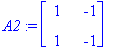
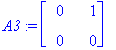
![[Vector(%id = 14422052), Matrix(%id = 12211076), Vector(%id = 14422132), Matrix(%id = 14560268), Vector(%id = 14422252), Matrix(%id = 13898300)]](images/L7maple96.gif)