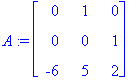Exa 3. Lineaarinen suodin (filtteri)
Warning, the name changecoords has been redefined
| > |
jana:=(p1,p2)->plot([p1,p2],color=blue):
yjana:=(x,y)->jana([x,0],[x,y]):
|
| > |
F:=(y,k)->a0*y(k+2)+a1*y(k+1)+a2*y(k);
|
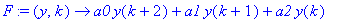
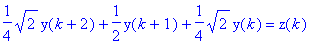
Tässä ajatellaan y(k) syötteeksi ja z(k) tulokseksi. (Differenssiyhtälöitä ratkaistaessa päinvastoin)
Valitaan ensin signaaliksi y(k) näytteitä kokonaislukuvälein funktiosta cos(Pi*t/4).
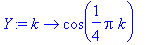
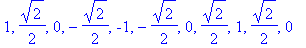
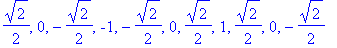
| > |
display(plot(Y(t),t=0..20),seq(yjana(k,Y(k)),k=0..40));
|
![[Maple Plot]](images/L5maple13.gif)
| > |
display(plot(Y(t),t=0..20),seq(yjana(k,F(Y,k)),k=0..40));
|
![[Maple Plot]](images/L5maple14.gif)
Signaali (Y(k)) menee filtterin läpi sellaisenaan muuten, paitsi siirtyy askeleen taaksepäin..
Pidetään sama näytteidenottoväli,
kasvatetaan
alkup. signaalin
taajuutta:
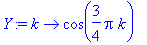
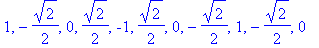
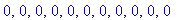
Kolminkertainen taajuus suodattui pois (näytteenottoväli pysyi samana).
Alipäästösuodin
.
| > |
display(plot(Y(t),t=0..10),seq(yjana(k,Y(k)),k=0..20));
|
![[Maple Plot]](images/L5maple18.gif)
| > |
display(plot(Y(t),t=0..10,axes=boxed),seq(yjana(k,F(Y,k)),k=0..20));
|
![[Maple Plot]](images/L5maple19.gif)
Yleisiä lauseita ja periaatteita
(EHY): Epähomogeeniyhtälö, (HY) Homogeeniyhtälö (oikea puoli = 0).
Lineaarikuvaus T:S--> S,
| > |
T(({y[k]}))={y[k+n]+sum(a[j]*y[k+n-j],j=1..n)}[k];
|
![T({y[k]}) = {y[k+n]+sum(a[j]*y[k+n-j],j = 1 .. n)}[k]](images/L5maple50.gif)
| > |
H=N(T); # T:n nolla-avaruus (ydin) on (EHY):n ratkaisujoukko.
|
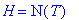
Lause 16
Lineaarisella n:nnen kertaluvun differyllä (a[n] # 0)
| > |
y[k+n]+sum(a[j]*y[k+n-j],j=1..n)=z[k];
|
![y[k+n]+sum(a[j]*y[k+n-j],j = 1 .. n) = z[k]](images/L5maple52.gif)
on jokaisella alkuarvojevektorin [
![y[0]](images/L5maple53.gif) , ...,
, ...,
![y[n-1]](images/L5maple54.gif) ] valinnalla yksikäsitteinen ratkaisu (
] valinnalla yksikäsitteinen ratkaisu (
![y[k]](images/L5maple55.gif) ).
).
Tod: Rekursiokaavasta voidaan yksikäsitteisesti laskea sekä eteenpäin että taaksepäin (jos tarpeen) miten pitkälle tahansa.
(Tarkemmin luennolla tai kirjassa(prujussa).)
Lause 17
Lineaarisen n:nnen kl:n (HY):n ratkaisuavaruuden dimensio = n.
Tod
: H=N(T) on aliavaruus. Osoitetaan, että dim(H)=n. Sitä varten muodostetaan lineaarikuvaus F: H ->
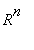 , joka osoitetaan
, joka osoitetaan
isomorfismiksi. Isomorfismi säilyttää kaikki VA-ominaisuudet, erityisesti dimension.
No, määritellään "projektiokuvaus" F: (
![y[k]](images/L5maple57.gif) ) -->(
) -->(
![y[0]](images/L5maple58.gif) , ... ,
, ... ,
![y[n-1]](images/L5maple59.gif) )
)
Osoitetaan, että F: H -->
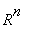 on isomorfismi. ts. lineaarinen bijektio.
on isomorfismi. ts. lineaarinen bijektio.
1) Lineaarisuus on hyvin selvä.
2) Surjektio & injektio: Olkoon (
![y[0]](images/L5maple61.gif) , . . .,
, . . .,
![y[n-1]](images/L5maple62.gif) ) mielivaltainen
) mielivaltainen
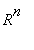 :n vektori. Lauseen 16 mukaan on olemassa 1-käs. ratkaisu (
:n vektori. Lauseen 16 mukaan on olemassa 1-käs. ratkaisu (
![y[k]](images/L5maple64.gif) ),
),
jonka koordinaatit 0,...,n-1 ovat nämä annetut. Olemassaolo tarkoittaa F:n surjektiivisuutta, yksikäsitteisyys injektiivisyyttä.
No niin, kuten sanottu, dim H = dim
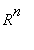 = n. [QED]
= n. [QED]
HY:n ratkaisumenetelmä: Etsitään n LRT ratkaisua.
Tämä on ratkaisuavaruuden kanta , joten kaikki ratkaisut ovat näiden lineaarikombinaatioia.
![yh[k] = sum(c[j]*y[j][k],j = 1 .. n)](images/L5maple66.gif)
Miten löydetään? Yrite
![y[k] = r^k](images/L5maple67.gif)
johtaa karakteristiseen polynomiyhtälöön ("auxiliary equation"):
![r^n+sum(a[j]*r^(n-j),j = 1 .. n) = 0](images/L5maple68.gif)
-
Yksinkertaiset reaalijuuret (eli n erillstä juurta). Helppo osoittaa, että tällöin ratkaisut (r[i]^k) ovat LRT ja siis ratkaisuavaruuden kanta. (Harj 4 AV)
-
Yksinkertaiset kompleksijuuret. Tällöin saadaan myös kanta aivan suoraan. Eulerin kaavan avulla siirrytään reaaliseen kantaan, jossa on sin/cos-termejä.
-
Moninkertaisia juuria. Tällöin tarvitaan a) temppuja tai b) teoriaa. Palataan ominaisarvojen yhteydessä.
EHY:n ratkaisumenetelmä: HY:n yleinen + EHY:n erikoinen
Lause.
(EHY):n kaikki ratkaisut ovat muotoa
![y = y[h]+y[p]](images/L5maple69.gif)
missä y[h] on HY:n yleinen ratkaisu (siis lineaarikombinaatio n:stä kantaratkaisusta) ja y[p] on jokin EHY:n (vaikkapa hatusta tempaistu) "erityis"ratkaisu.
(p niinkuin "particular")
Tod: Perustuu pelkästään lineaarisuuteen. (Aivan sama lause pätee vaikkapa tavalliselle lineaariselle yhtälösysteemile.)
1) Olkoon H (EHY):n ratkaisuavaruus ja
![y[h]*epsilon*H](images/L5maple70.gif)
![T(y[h]+y[p]) = T(y[h])+T(y[p])](images/L5maple71.gif)
Tämä = z, koska
![T(y[h]) = 0](images/L5maple72.gif) ja
ja
![T(y[p]) = z](images/L5maple73.gif) .
.
Siis mielivaltainen väitettyä muotoa oleva summa on EHY:n ratkaisu.
2) Olkoon nyt y mielivaltainen EHY:n ratkaisu.
Tällöin
![y-y[p]*epsilon*H](images/L5maple74.gif)
sillä
![T(y-y[p]) = 0](images/L5maple75.gif)
koska
![T(y-y[p]) = T(y)-T(y[p])](images/L5maple76.gif)
ja molemmat viimemainitut ovat = z.
Siispä
![y-y[p] = y[h]](images/L5maple77.gif)
missä
![y[h]](images/L5maple78.gif) on jokin HY:n ratkaisu.
on jokin HY:n ratkaisu.
Niinpä mielivaltaisesti annettu EHY:n ratkaisu
y
voitiin kirjoittaa vaaditussa muodossa.
Lineaarinen differyhtälösysteemi
Aivan samoin, kuten näemme differentiaaliyhtälöiden kohdalla, myös differenssiyhtälöiden teoria ja käytäntö kannattaa opetella
palauttamaan systeemien käsittelyyn. (Tämä on ns. "moderni" käsittelytapa.)
-
Jokainen n:nnen kertaluvun yhtälö palautuu 1. kertaluvun nxn-systeemiin.
-
Systeemien teoria on kiintoisaa sinänsä (kaikki systeemit eivät ole peräisin jostain n:nnen kertaluvun yhtälöstä).
Lineaarisen homogeenisen systeemin yleinen muoto:
![x[k+1] = A*x[k]](images/L5maple79.gif)
missä A on nxn-matriisi (
![x[k]](images/L5maple80.gif) on
on
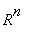 :n vektori.)
:n vektori.)
Esim. 7. Muuntaminen systeemiksi.
| > |
![y[k+3]-2*y[k+2]-5*y[k+1]+6*y[k] = 0](images/L5maple82.gif)
|
![y[k+3]-2*y[k+2]-5*y[k+1]+6*y[k] = 0](images/L5maple83.gif)
Merkitään
![x[k] = Vector(%id = 12583436)](images/L5maple84.gif)
![x[k+1] = Vector(%id = 12758760)](images/L5maple85.gif)
y[k+3] lasketaan yhtälöstä:
![x[k+1] = Vector(%id = 12583596)](images/L5maple86.gif)
Siis
| > |
![x[k+1] = A*x[k]](images/L5maple87.gif)
|
![x[k+1] = A*x[k]](images/L5maple88.gif)
missä
| > |
A:=<<0,0,-6>|<1,0,5>|<0,1,2>>;
|
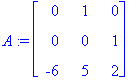
Jos onnistumme ratkaisemaan tämän 1. kertaluvun systeemin, niin ratkaisuvektorin
![x[k]](images/L5maple90.gif) 1. koordinaatti antaa yhtälön ratkaisukoordinaatin
1. koordinaatti antaa yhtälön ratkaisukoordinaatin
![y[k]](images/L5maple91.gif) .
.
![]()
![[Maple Plot]](images/L5maple2.gif)
![]()
![[Maple Plot]](images/L5maple4.gif)
![[Maple Plot]](images/L5maple5.gif)
![[Maple Plot]](images/L5maple6.gif)
![[Maple Plot]](images/L5maple13.gif)
![[Maple Plot]](images/L5maple14.gif)
![[Maple Plot]](images/L5maple18.gif)
![[Maple Plot]](images/L5maple19.gif)
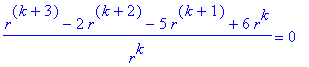
![T({y[k]}) = {y[k+n]+sum(a[j]*y[k+n-j],j = 1 .. n)}[k]](images/L5maple50.gif)
![y[k+n]+sum(a[j]*y[k+n-j],j = 1 .. n) = z[k]](images/L5maple52.gif)
![yh[k] = sum(c[j]*y[j][k],j = 1 .. n)](images/L5maple66.gif)
![r^n+sum(a[j]*r^(n-j),j = 1 .. n) = 0](images/L5maple68.gif)
![x[k] = Vector(%id = 12583436)](images/L5maple84.gif)
![x[k+1] = Vector(%id = 12758760)](images/L5maple85.gif)
![x[k+1] = Vector(%id = 12583596)](images/L5maple86.gif)