10.1 Jaksolliset funktiot, trigonometriset sarjat
Perusteet kirjassa ja luennolla
Lyhyesti: f: R -> R on jaksollinen, jaksona p>0, jos
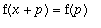 kaikilla
kaikilla
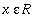 .
.
Pienin p on perusjakso.
Jos f on p-jaksoinen, niin se on
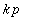 -jaksoinen kaikilla
-jaksoinen kaikilla
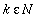 .
.
(Kaikilla jaksollisilla ei ole pienintä, vakiofunktio on jaksollinen ja kaikki p>0 ovat jaksoja.)
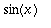 ,
,
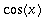 ovat
ovat
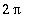 - jaksoisia.
- jaksoisia.
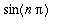 ,
,
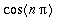 ovat
ovat
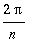 - jaksoisia.
- jaksoisia.
Tutkimme sarjaa:
| > |
![a[0]+Sum(a[n]*cos(n*x)+b[n]*sin(n*x),n = 1 .. infinity)](images/L16four11.gif)
|
Jaksollinen jatkaminen
Jokainen jollain välillä [a,b] määritelty funktio voidaan jatkaa jaksollisena (p=b-a) koko R:ään.
Hyvä, että meillä on Maple-funktio
JJ
sitä varten.
Esim:
| > |
f:=x->x^2: # välillä [0,1], jatka 1-jaksoisena!
|
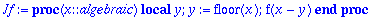
![[Maple Plot]](images/L16four13.gif)
| > |
f:=x->x^2: # välillä [-1,1], jatka 2-jaksoisena!
|

![[Maple Plot]](images/L16four15.gif)
Esim. Kanttiaaltoja saa kätevästi Heavisiden funktion jaksollisena jatkona.
| > |
with(inttrans): alias(u=Heaviside):
|
![[Maple Plot]](images/L16four16.gif)
| > |
plot(2*Ju-1,-2..2,scaling=constrained,axes=boxed);
|
![[Maple Plot]](images/L16four17.gif)
Ehkä helpompaa on määritellä näin:
| > |
f:=x->piecewise(x>0,1,x<0,-1);
|
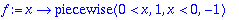
| > |
Jf:=JJ(f,-1..1): plot(Jf,-2..2);
|
![[Maple Plot]](images/L16four19.gif)
Kaikkein helpointa on käyttää
signum
-funktiota, vrt. yllä.
10.2 Fourier-sarjojen laskeminen
| > |
Sis:=(f,g)->int(f(x)*g(x),x=-Pi..Pi);
|
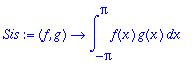
Palautetaan mieleen sisätuloavaruuden vektorin esitys ON kannan suhteen
Olkoon
![{e[1], e[2] .. e[m]}](images/L16four21.gif) ON kanta sisätuloavaruudessa V. Olkoon v jokin vektori V:ssä.
ON kanta sisätuloavaruudessa V. Olkoon v jokin vektori V:ssä.
![v = Sum(c[j]*e[j],j = 1 .. m)](images/L16four22.gif) . Määrätään kertoimet
. Määrätään kertoimet
![c[j]](images/L16four23.gif) .
.
Sehän tapahtui näin: Kerrotaan yhtälö puolittain sisätulon mielessä
![e[k]](images/L16four24.gif) :lla,
:lla,
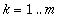 :
:
![`<,>`(v,e[k]) = Sum(c[j]*`<,>`(e[j],e[k]),j = 1 .. m)](images/L16four26.gif) .
.
Summassa on vain yksi nollasta poikkeava termi =
![c[k]*`<,>`(e[k],e[k])](images/L16four27.gif) , joka = 1, joten
, joka = 1, joten
![c[k] = `<,>`(v,e[k])](images/L16four28.gif) .
.
Siispä
![v = Sum(`<,>`(v,e[j])*e[j],j = 1 .. m)](images/L16four29.gif)
Tätähän kutsuimme edellä jo Fourier-esitykseksi.
Muista myös toinen näkökulma:
Jos
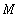 on sisätuloavaruuden
on sisätuloavaruuden
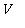 aliavaruus ja jos
aliavaruus ja jos
![{e[1], e[2] .. e[m]}](images/L16four32.gif) on
on
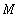 :n ON kanta, niin mielivaltaisen vektorin
:n ON kanta, niin mielivaltaisen vektorin
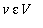 paras approksimaatio aliavaruudessa
paras approksimaatio aliavaruudessa
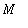 (PNS-approksimaatio) on
(PNS-approksimaatio) on
v* =
![Sum(`<,>`(v,e[j])*e[j],j = 1 .. m)](images/L16four36.gif)
Trigonometrisen systeemin ortogonaalisuus
| > |
cos((n+k)*x): %=expand(%);
|
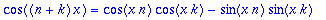
| > |
cos((n-k)*x): %=expand(%);
|
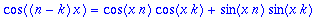
| > |
cosyht:=cos(x*n)*cos(x*k)=1/2*(cos((n+k)*x)+cos((n-k)*x));
|
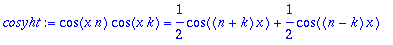
| > |
sinyht:=sin(x*n)*sin(x*k)=1/2*(cos((n-k)*x)-cos((n+k)*x));
|
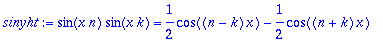
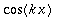 _|_
_|_
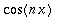 , kun
, kun
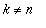 :
:
| > |
Int(lhs(cosyht),x=-Pi..Pi)=int(rhs(cosyht),x); # jos n erisuuri kuin k.
|
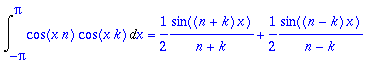
missä oikealla sijoitetaan
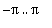 . Saadaan siis 0.
. Saadaan siis 0.
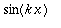 _|_
_|_
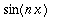 , kun
, kun
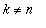 :
:
Aivan samoin saadaan nolla, kun
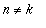 siniyhtälössä:
siniyhtälössä:
| > |
Int(lhs(sinyht),x=-Pi..Pi)=int(rhs(sinyht),x); # jos n erisuuri kuin k.
|
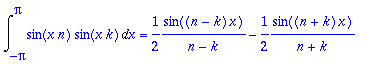
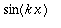 _|_ 1 ,
_|_ 1 ,
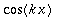 _|_ 1 , kun k > 0:
_|_ 1 , kun k > 0:
| > |
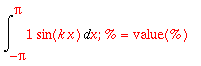
|
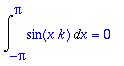
| > |
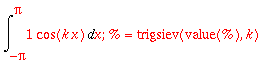
|
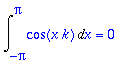
| > |
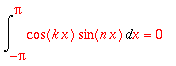
|
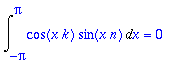
koska
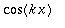 on parillinen fkt. ja
on parillinen fkt. ja
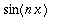 pariton.
pariton.
Siten niiden tulo on pariton, joten integraali O:n suhteen symmetrisen välin yli on = 0.
Osoitimme siis, että trigonometrinen systeemi
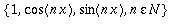 on ortogonaalinen.
on ortogonaalinen.
Lasketaan vielä normit:
| > |
(cos(k*x))^2=combine(cos(k*x)^2);
|
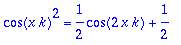
| > |
int(rhs(%),x=-Pi..Pi);trigsiev(%,k);
|
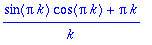

| > |
#trigsiev #(read("polku/v302.mpl"):)
|
| > |
sin(k*x)^2=combine(sin(k*x)^2);
|
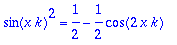
| > |
int(rhs(%),x=-Pi..Pi);trigsiev(%,k);
|
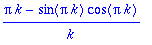

Molemmista saatiin siis
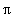 , joten ||
, joten ||
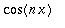 || = ||
|| = ||
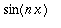 || =
|| =
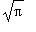 .
.
|| 1 || =
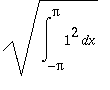 , joka on
, joka on
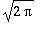 .
.
Fourier-kertoimet
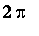 -jaksoiset funktiot
-jaksoiset funktiot
Koska trigonometrinen systeemi on ortogonaalinen, voimme käyttää kertoimien johtamisessa aivan samaa tekniikkaa,
kuin edellä. Nyt on vain kyse sarjasta ja tehtävänasettelu on tämä: Oletetaan, että
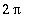 -jaksoinen funktio f: R --> R
-jaksoinen funktio f: R --> R
voidaan esittää suppenevan sarjan summana muodossa:
(1)
![f(x) = a[0]+Sum(a[n]*cos(n*x)+b[n]*sin(n*x),n = 1 .. infinity)](images/L16four76.gif) .
.
Oletetaan lisäksi, että sarjan integrointi termeittäin on sallittua. Tällöin kertoimien lausekkeet ovat välttämättä alla olevat.
Päättely on nyt aivan sama kuin yllä: Kun määrätään kerrointa
![a[k]](images/L16four77.gif) tai
tai
![b[k]](images/L16four78.gif) , niin kerrotaan yhtälö puolittain vastaavalla
, niin kerrotaan yhtälö puolittain vastaavalla
kantafunktiolla ja integroidaan yli välin [-
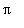 ,
,
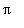 ]. Ts. kerrotaan puolittain sisätulon mielessä ko, kantafunktiolla.
]. Ts. kerrotaan puolittain sisätulon mielessä ko, kantafunktiolla.
Ortogonaalisuuden ansiosta summaan jää vain yksi nollasta poikkeava termi (summausindeksin n arvolla k, tai jos k=0,
jolloin lasketaan
![a[0]](images/L16four81.gif) :aa, jää pelkkä
:aa, jää pelkkä
![a[0]*`<,>`(1,1)](images/L16four82.gif) - termi (eli
- termi (eli
![a[0]*2*Pi](images/L16four83.gif) ).)
).)
Näihin kaavoihin siis johdutaan. Kaavat johti jo kauan ennen
Fourieria
, kukas muu kuin
Euler
v. 1777.
| > |
a0:=(1/(2*Pi))*Int(f(x),x=-Pi..Pi);
|
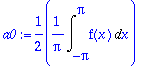
| > |
an:=(1/Pi)*Int(f(x)*cos(n*x),x=-Pi..Pi);
|
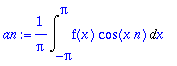
| > |
bn:=(1/Pi)*Int(f(x)*sin(n*x),x=-Pi..Pi);
|
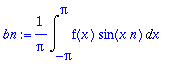
| > |
sarja:='a0'+Sum('an'*cos(n*x)+'bn'*sin(n*x),n=1..infinity);
|
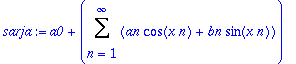
| > |
osasumma:=(x,N)->a0+add(an*cos(n*x)+bn*sin(n*x),n=1..N):
|
Fourier
-sarjojen muodostaminen on nyt helppoa. Toki voi tulla integrointivaivaa, mutta Maplea voi käyttää
nautinnollisesti hyödyksi. Voi tietysti syntyä myös tilanteita, joissa on turvauduttava numeeriseen integrointiin.
Siihenkin Maplessa on välineitä.
Esim. Kanttiaalto (KRE Exa 1 s. 532)
| > |
kantti:=JJ(signum,-Pi..Pi); # Tehdään nyt helpoimmalla tavalla.
|
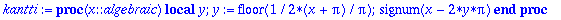
| > |
plot(kantti(x),x=-2*Pi..2*Pi);
|
![[Maple Plot]](images/L16four89.gif)
Voitaisiin käyttää
signum
-funktiota tai
piecewise
-määrittelyä, tms. yleisissä kaavoissa, mutta tehdään, kuten käsin laskiessa.
| > |
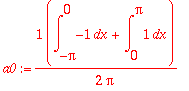
|
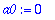
| > |
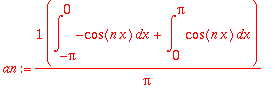
|
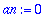
Koska funktio f on pariton, ja
![a[n]](images/L16four94.gif) -kertoimien kaavassa se kerrotaan parillisella funktiolla (1 tai cos), on integroitava pariton, ja tulos siten 0.
-kertoimien kaavassa se kerrotaan parillisella funktiolla (1 tai cos), on integroitava pariton, ja tulos siten 0.
| > |
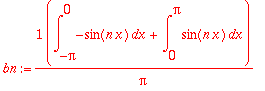
|
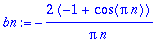
Integroitava on nyt parillinen (pariton x pariton), joten voidaan
laskea myös näin:
| > |
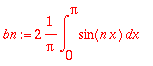
|
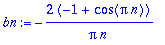
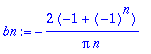
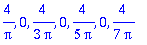
| > |
sarja:='a[0]'+Sum('a[n]'*cos(n*x)+'b[n]'*sin(n*x),n=1..infinity);
|
![sarja := a[0]+Sum(a[n]*cos(x*n)+b[n]*sin(x*n),n = 1 .. infinity)](images/L16four101.gif)
| > |
osasumma:=(x,N)->add(bn*sin(n*x),n=1..N);
|

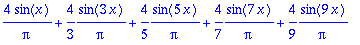
| > |
sarja:=(4/Pi)*Sum(sin(2*k-1)*x/(2*k-1),k=1..infinity); # Muista iso Sum !
|
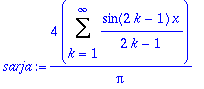
Kuvaajia:
| > |
plot([kantti(x),osasumma(x,1)],x=-2*Pi..2*Pi);
|
![[Maple Plot]](images/L16four105.gif)
| > |
plot([kantti(x),seq(osasumma(x,N),N=1..11)],x=-2*Pi..2*Pi);
|
![[Maple Plot]](images/L16four106.gif)
| > |
plot([kantti(x),seq(osasumma(x,N),N=[1,3,5,31,67])],x=-2*Pi..2*Pi,color=[gray,black,green,blue,red]);
|
![[Maple Plot]](images/L16four107.gif)
| > |
plots[display](%,view=[-Pi..Pi,-1.5..1.5]);
|
![[Maple Plot]](images/L16four108.gif)
| > |
plot([kantti(x),osasumma(x,101)],x=-0.1..Pi+.1,color=[gray,blue],numpoints=100);
|
![[Maple Plot]](images/L16four109.gif)
| > |
display(%,view=[0..Pi,0.7..1.3]);
|
![[Maple Plot]](images/L16four110.gif)
Fourier-sarjojen suppeneminen
Jos on annettu
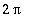 - jaksoinen integroituva f: R->R, voidaan aina muodostaa Fourier-kertoimet
- jaksoinen integroituva f: R->R, voidaan aina muodostaa Fourier-kertoimet
![a[n]](images/L16four112.gif) ,
,
![b[n]](images/L16four113.gif) ja siten Fourier-sarja
ja siten Fourier-sarja
![a[0]+Sum(a[n]*cos(n*x)+b[n]*sin(n*x),n = 1 .. infinity)](images/L16four114.gif) .
.
Kysymys1: Suppeneeko sarja
Kysymys 2: Jos suppenee, niin esittääkö funktiota f.
Usein merkitään:
f (x) ~
![a[0]+Sum(a[n]*cos(n*x)+b[n]*sin(n*x),n = 1 .. infinity)](images/L16four115.gif)
Suppenemislauseet ovat yleensä vaikeita ja syvällisiä. Teoreettiset kysymykset ovat vaikeita, käytännön laskut ja soveltaminen helppoa.
Välttämättömiä ja riittäviä suppenemisehtoja ei vieläkään tunneta.
Sensijaan käyttökelpoisia riittäviä ehtoja on tarjolla. Tässä oikein sopiva:
Lause.
(KRE s. 535 Thm 1) Jos
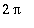 - jaksoinen f: R-->R on paloittain jatkuva välillä [
- jaksoinen f: R-->R on paloittain jatkuva välillä [
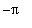 ,
,
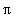 ] ja jos sillä on v.p. ja o.p. derivaatat (*) kaikissa
] ja jos sillä on v.p. ja o.p. derivaatat (*) kaikissa
välin pisteissä, niin f:n Fourier-sarja suppenee
-
pisteissä x, joissa f on jatkuva, kohti arvoa f(x) ja
-
pisteissä x, joissa f:llä on hyppy, kohti arvoa
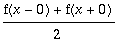 .
.
Huom! v.p. ja o.p. derivaatta tarkoittavat tässä yhteydessä tavanomaisten käsitteiden lievennystä sikäli, että derivaatan laskentapisteeksi
otetaan vastaava v.p. tai o.p. raja-arvo. Niinpä tässä tarkoitetussa mielessä esim. Heavisiden funktiolla u(x) on 0:ssa v.p. ja o.p. derivaatat,
ja molemmat ovat = 0. Varsinaisessa mielessä näin ei ole, määriteltiinpä u(0) miten tahansa. (Jos olisi, niin u:lla olisi derivaatta 0:ssa, ja se
romuttaisi hyvän osan ykköskurssien oppeja.)
Tämä on tärkeä "pointti", sillä näin saamme lauseen piiriin juuri porrasfunktioita yms. "kanttikäytöksiä".
KRE-kirjassa annetaan lauseelle
todistus
vahventamalla huomattavasti oletuksia ja lieventämällä johtopäätöstä. (Pelkkä suppenemsitodistus
ilman mitään yritystäkään siihen, esittääkö summa f(x):ää (kirjallisuusviite kylläkin ja maininta syvällisyydestä).
Koska jälkimmäinen on juuri se olennainen, päätämme jättää tämän todistuksen väliin, sinänsä se ei ole lainkaan vaikea (mutta siis aika hyödytön).
Katsotaan suppenemislauseen kannalta uudestaan kanttiaallon F-sarjaa.
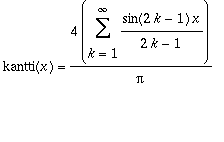 .
.
| > |
kantti(Pi/2)=4/Pi*(1-1/kolme+1/viisi-1/seitseman+ooo);
|
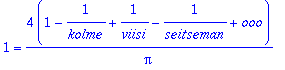
Saadaan
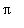 :lle sarjakehitelmä:
:lle sarjakehitelmä:
| > |
Pi=4*(Sum((-1)^(k-1)/(2*k-1),k=1..infinity));
|
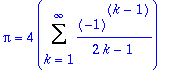
Tämän sarjan johti Leibniz 1673. Fourier-sarjalauseiden voimaa kuvastaa se, että niiden avulla saadaan sivutuotteena erinäisten vakiotermisten
sarjojen summia. (Sarjan summan määrittäminenhän on yleensä paljon vaikeampaa kuin pelkän suppenemisen osoitteminen.)
Mielivaltainen jakso
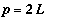
Saadaan edellisestä skaalaamalla: Otetaan uusi muuttuja
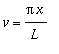 .
.
Jos f on 2*L-jaksoinen, saadaan näin kaavat:
![f(x) = a[0]+Sum(a[n]*cos(n*Pi*x/L)+b[n]*sin(n*Pi*x/L),n = 1 .. infinity)](images/L16four126.gif)
missä
![a[0] = Int(f(x),x = -L .. L)/(2*L)](images/L16four127.gif)
![a[n] = 1/L*Int(f(x)*cos(n*Pi*x/L),x = -L .. L)](images/L16four128.gif)
![b[n] = 1/L*Int(f(x)*sin(n*Pi*x/L),x = -L .. L)](images/L16four129.gif)
Esim: Puoliaaltotasasuunnattu siniaalto
Sinisarja ja kosinisarja
Jäljempänä esitämme parillisen ja parittoman laajennusoperaattorin. Käytännössä parillista/paritonta laajennusta vastaa kosini/sinisarja, jossa lähdetään liikkeelle välillä [0,d] määritellystä funktiosta f, joka laajennetaan parilliseksi/parittomaksi. Tällöin yllä olevat kaavat tulevat muotoon:
1) kosinisarja:
| > |
f:='f': T:='T': omega:='omega': #omega:=2*Pi/T:
|
| > |
a0:=(1/d)*int(f(t),t=-d..d);an:=(1/d)*int(f(t)*cos(n*omega*t),t=-d..d);bn:=0;
|
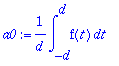
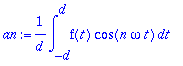
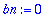
Koska yllä olevat integroitavat ovat parilllisia, voidaan integroida [0..d], kunhan tulos kerrotaan 2:lla.
Tällöin tullaan toimeen alkuperäisellä, välillä [0,d] määritellyllä funktiolla, eikä tarvitse kohdistaa integrointia parilliseen laajennukseen. Siispä
kosinisarjakaavat
ovat:
| > |
f:='f':T:='T':omega:='omega':#omega:=2*Pi/T:
a0:=(2/d)*int(f(t),t=0..d);
an:=(2/d)*int(f(t)*cos(n*omega*t),t=0..d);bn:=0;
sarja:='a0'/2+sum('an'*cos(n*omega*t),n=1..infinity);
|
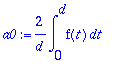
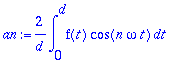
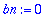
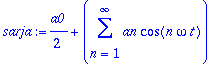
Sinisarja
saadaan aivan vastaavasti:
| > |
f:='f':T:='T':omega:='omega':#omega:=2*Pi/T:
bn:=(2/d)*int(f(t)*sin(n*omega*t),t=0..d);
sarja:=sum('bn'*cos(n*omega*t),n=1..infinity);
|
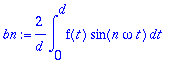
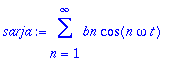
Kompleksinen muoto
Kokeillaan vaihteeksi sellaista tyyliä, että c on n:n funktio, tässä se on mukavaa, kun kaavatkin ovat yhtenäiset. c-funktio on syytä määritellä unapply-tavalla. Laskentatehossa nimittäin on dramaattinen ero. (unapply evaluoi (esim. integroi) määrittelyaikana, kun taas -> määrittely tekee sen kutsuaikana.)
| > |
T:='T': f:='f': omega:='omega': omega:=2*Pi/T:
|
| > |
c:=unapply(1/T*int(f(t)*exp(-I*n*omega*t),t=0..T),n);c(0):=1/T*int(f(t),t=0..T);
|
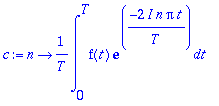
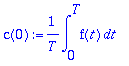
Vaikka seuraava toimii, niin ei kannata tehdä, kts. yllä.
| > |
#c:=n->1/T*int(f(t)*exp(-I*n*omega*t),t=0..T);
|
| > |
# sarja:=sum('c(n)'*exp(I*n*'omega'*t),n=-infinity..infinity);
|
Esim.
Muodosta alla määriteltävän funktion Fourier-sarja, piirrä jaksollinen laajennus ja Fourier-osasummien kuvaajia. Piirrä myös taajuusspektrit. Käsittele sekä reaalimuotoista sin/cos-sarjaa että kompleksimuotoista.
| > |
f:=t->piecewise(-Pi<t and t < 0,t+Pi,0<t and t<Pi,Pi);
|
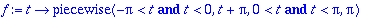
![[Maple Plot]](images/L16four142.gif)
| > |
plot(jaksf,-2*Pi..2*Pi);
|
![[Maple Plot]](images/L16four143.gif)
| > |
a0:=(2/T)*int(f(t),t=-Pi..Pi);
an:=(2/T)*int(f(t)*cos(n*omega*t),t=-Pi..Pi):an:=trigsiev(an,n);
bn:=(2/T)*int(f(t)*sin(n*omega*t),t=-Pi..Pi):bn:=trigsiev(bn,n);
|
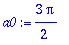
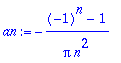
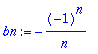
Koska halusimme välttyä
assume
-komennon aiheuttamilta sivuvaikutuksilta, sievensimme omalla
trigsiev-
komennolla. Huomaamme, että
int
osasi käsitellä
piecewise
-määriteltyä funktiota ihan nätisti. Luultavaa on, että se osaa myös epäjatkuvalle, mutta kannattaa tarkkailla.
| > |
#sarja:=a0/2+sum(an*cos(n*omega*t)+bn*sin(n*omega*t),n=1..infinity);
|
| > |
osasumma:=N->a0/2+sum(an*cos(n*omega*t)+bn*sin(n*omega*t),n=1..N);
|
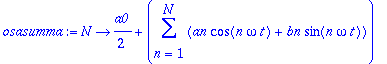
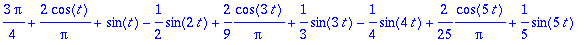
Tässä tyylissä (jossa an ja bn integroitiin symbolisesti valmiiksi), on aivan sopivaa (ja suositeltavaa) käyttää -> funktiomääritystapaa.
| > |
plot([jaksf(t),osasumma(10)],t=-2*Pi..2*Pi);
|
![[Maple Plot]](images/L16four149.gif)
| > |
plot([jaksf(t),seq(osasumma(k),k=1..10)],t=-2*Pi..2*Pi);
|
![[Maple Plot]](images/L16four150.gif)
Taajuusspekrit:
Piirtäminen hoituu oikein näppärästi yllä määrittelemällämme
jana
-funktiolla.
| > |
A0:=a0/2; An:=abs(an-I*bn);
|
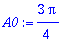
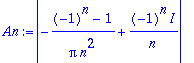
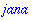
| > |
phi0:=0: phin:=argument(an-I*bn);
|
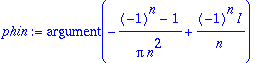
| > |
display([jana(0,A0),seq(jana(n,An),n=1..6)],axes=box,title="Amplitudispektri");display([jana(0,phi0),seq(jana(n,phin),n=1..6)],title="Vaihespektri");
|
![[Maple Plot]](images/L16four155.gif)
![[Maple Plot]](images/L16four156.gif)
Kompleksinen muoto
| > |
c:=unapply(1/T*int(f(t)*exp(-I*n*omega*t),t=0..T),n);c(0):=1/T*int(f(t),t=0..T);
|
| > |
sarja:=sum('c(n)'*exp(I*n*'omega'*t),n=-infinity..infinity);
|
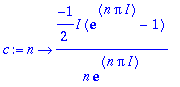
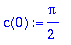
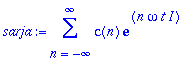
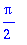
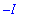
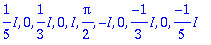
| > |
display([seq(jana(n,abs(c(n))),n=-6..6)],axes=box,title="Amplitudispektri");
|
![[Maple Plot]](images/L16four163.gif)
| > |
display([seq(jana(n,argument(c(n))),n=-6..6)],title="Vaihespektri");
|
![[Maple Plot]](images/L16four164.gif)
![]() kaikilla
kaikilla
![]() .
.
![]() -jaksoinen kaikilla
-jaksoinen kaikilla
![]() .
.
![]() ,
,
![]() ovat
ovat
![]() - jaksoisia.
- jaksoisia.
![]() ,
,
![]() ovat
ovat
![]() - jaksoisia.
- jaksoisia.
![a[0]+Sum(a[n]*cos(n*x)+b[n]*sin(n*x),n = 1 .. infinity)](images/L16four11.gif)
![]()
![[Maple Plot]](images/L16four13.gif)
![]()
![[Maple Plot]](images/L16four15.gif)
![[Maple Plot]](images/L16four16.gif)
![[Maple Plot]](images/L16four17.gif)
![]()
![[Maple Plot]](images/L16four19.gif)
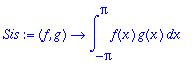
![v = Sum(c[j]*e[j],j = 1 .. m)](images/L16four22.gif) . Määrätään kertoimet
. Määrätään kertoimet
![`<,>`(v,e[k]) = Sum(c[j]*`<,>`(e[j],e[k]),j = 1 .. m)](images/L16four26.gif) .
.
![v = Sum(`<,>`(v,e[j])*e[j],j = 1 .. m)](images/L16four29.gif)
![Sum(`<,>`(v,e[j])*e[j],j = 1 .. m)](images/L16four36.gif)
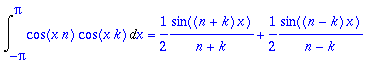
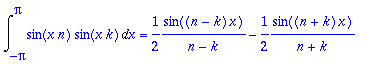
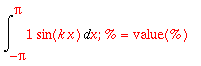
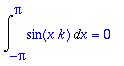
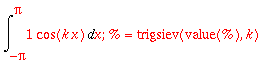
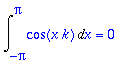
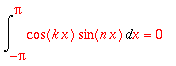
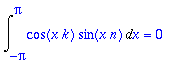
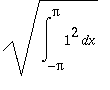 , joka on
, joka on
![f(x) = a[0]+Sum(a[n]*cos(n*x)+b[n]*sin(n*x),n = 1 .. infinity)](images/L16four76.gif) .
.
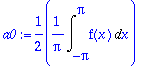
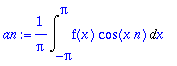
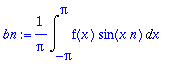
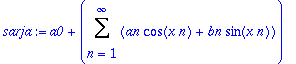
![[Maple Plot]](images/L16four89.gif)
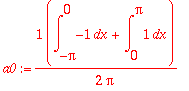
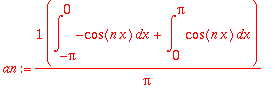
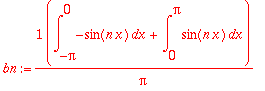
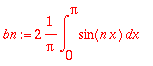
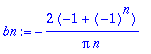
![sarja := a[0]+Sum(a[n]*cos(x*n)+b[n]*sin(x*n),n = 1 .. infinity)](images/L16four101.gif)
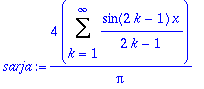
![[Maple Plot]](images/L16four105.gif)
![[Maple Plot]](images/L16four106.gif)
![[Maple Plot]](images/L16four107.gif)
![[Maple Plot]](images/L16four108.gif)
![[Maple Plot]](images/L16four109.gif)
![[Maple Plot]](images/L16four110.gif)
![a[0]+Sum(a[n]*cos(n*x)+b[n]*sin(n*x),n = 1 .. infinity)](images/L16four114.gif) .
.
![a[0]+Sum(a[n]*cos(n*x)+b[n]*sin(n*x),n = 1 .. infinity)](images/L16four115.gif)
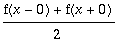 .
.
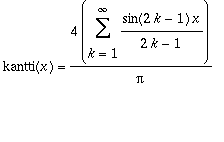 .
.
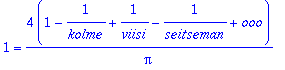
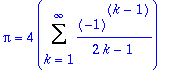
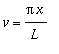 .
.
![f(x) = a[0]+Sum(a[n]*cos(n*Pi*x/L)+b[n]*sin(n*Pi*x/L),n = 1 .. infinity)](images/L16four126.gif)
![a[0] = Int(f(x),x = -L .. L)/(2*L)](images/L16four127.gif)
![a[n] = 1/L*Int(f(x)*cos(n*Pi*x/L),x = -L .. L)](images/L16four128.gif)
![b[n] = 1/L*Int(f(x)*sin(n*Pi*x/L),x = -L .. L)](images/L16four129.gif)
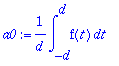
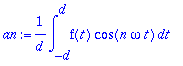
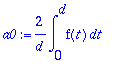
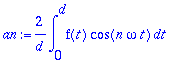
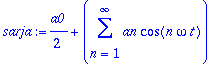
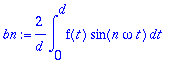
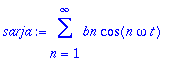
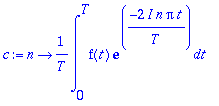
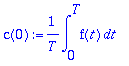
![[Maple Plot]](images/L16four142.gif)
![[Maple Plot]](images/L16four143.gif)
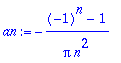
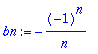
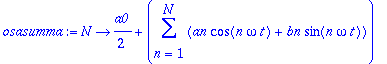
![[Maple Plot]](images/L16four149.gif)
![[Maple Plot]](images/L16four150.gif)
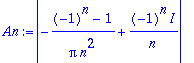
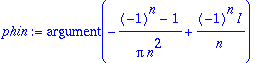
![[Maple Plot]](images/L16four155.gif)
![[Maple Plot]](images/L16four156.gif)
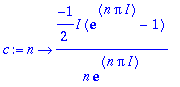
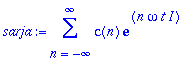
![[Maple Plot]](images/L16four163.gif)
![[Maple Plot]](images/L16four164.gif)
![[Maple Plot]](images/L16four166.gif)
![[Maple Plot]](images/L16four167.gif)
![[Maple Plot]](images/L16four168.gif)
![[Maple Plot]](images/L16four169.gif)
![[Maple Plot]](images/L16four171.gif)
![osasumma := proc (N) options operator, arrow; sum(b[n]*sin(n*omega*t),n = 1 .. N) end proc](images/L16four172.gif)
![[Maple Plot]](images/L16four175.gif)