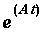
L13maple,
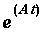
Alustukset
| > | restart: |
Warning, the name changecoords has been redefined
| > | with(LinearAlgebra):with(linalg): |
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
| > | alias(GS=LinearAlgebra[GramSchmidt]): |
Esim. EHY-ratk.
Luentotehtävä
| > | A:=<<2,1>|<-4,-3>>; |
![]()
| > | g:=t-><2*t^2+10*t,t^2+9*t+3>; |
![]()
| > | (lambda,ov):=Eigenvectors(A); |
![]()
| > | v1:=ov[1..-1,1]: v2:=ov[1..-1,2]: |
| > | yh:=C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2; |
| > |
![]()
| > |
LinearAlgebra on keskeneräinen. Yllä oleva täytyy tarjoilla komponentti kerrallaan:
| > | Y:=t-><<exp(lambda[1]*t)*v1[1],exp(lambda[1]*t)*v1[2]>|<exp(lambda[2]*t)*v2[1],exp(lambda[2]*t)*v2[2]>>; |
![]()
| > | Y(t); |
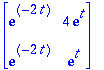
Tässä on nyt perusmatriisi . Sen avulla sa
adaan
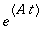 .
.
| > | expA:=t->Y(t).(Y(0)^(-1)); |
![]()
| > | expA(t); |
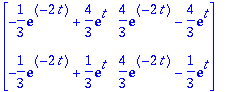
| > | exponential(A,t); |
![matrix([[-1/3*exp(-2*t)+4/3*exp(t), 4/3*exp(-2*t)-4/3*exp(t)], [-1/3*exp(-2*t)+1/3*exp(t), 4/3*exp(-2*t)-1/3*exp(t)]])](images/L13maple11.gif)
Oikein meni.
Sitten se kaunis EHY-kaava :
| > | y(t)=e^('A'*t)*C+Int(e^'A(t-s)'*'g(s)',s=0..t); #tekstinkäsittelyä |
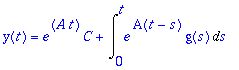
| > | yp:=map(int,expA(t-s).g(s),s=0..t); |
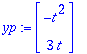
Saatiin kuin saatiinkin sama tulos kuin eilen lasketulla yritteellä (vrt. KRE 3.6 s. 184)
| > | yh:=expA(t).<C1,C2>;yh:=map(collect,%,{exp(-2*t),exp(t)}); |
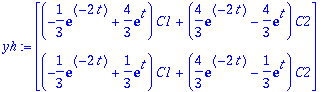
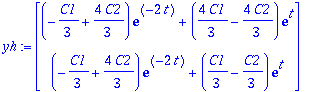
| > | y:=yh+yp; |
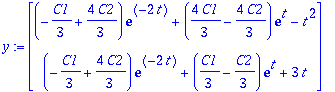
| > |
| > |
Saadaan yksinkertaisempaan muotoon, tee käsin!