L12maple.mws
Lineaariset differentiaaliyhtälösysteemit. Ke 30.10-ti 5.11.02
Alustukset
| > |
with(LinearAlgebra):with(linalg):
|
Warning, the assigned name GramSchmidt now has a global binding
Warning, the name adjoint has been redefined
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
| > |
with(plots): with(DEtools):
|
Warning, the name adjoint has been redefined
Seosprobleema
| > |
with(LinearAlgebra):with(linalg):
|
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
| > |
A:=<<-1/10,1/10>|<3/40,-1/5>>;
|
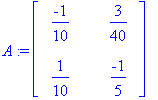
| > |
(lambda,ov):=Eigenvectors(A);
|
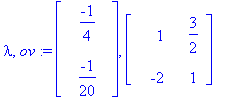
| > |
x:=[ov[1..-1,1],ov[1..-1,2]];
|
![x := [Vector(%id = 20022384), Vector(%id = 20022944)]](images/L12maple3.gif)
| > |
Yh:=C1*exp(lambda[1]*t)*x[1]+C2*exp(lambda[2]*t)*x[2];
|
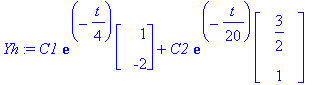
HY-yrite: Yksinkertaisinta on yrittää vakiovektoria y=v;
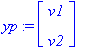
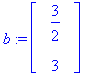
| > |
map(diff,yp,t)='A.yp'+b;
|
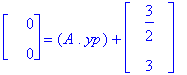
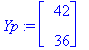
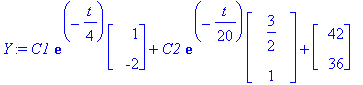
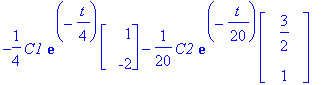
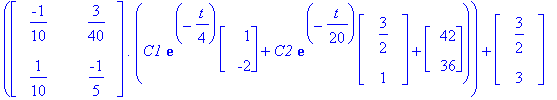
Tarkistaminen vektorimuodossa ei käykään helposti, Maplen tietorakenteet tekevät tenän.
No, jatketaan ja jätetään tarkistus loppuun.
| > |
AE:=subs(t=0,Y)=<25,15>;AE:=map(eval,%);
|
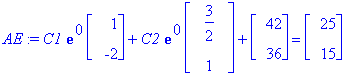
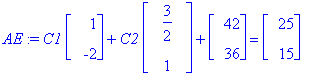
![vector([C1+3/2*C2+42, -2*C1+C2+36])](images/L12maple14.gif)
| > |
Ceet:=LinearSolve(<<1,-2>|<3/2,1>>,<25-42,15-36>);
|
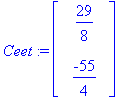
| > |
Y:=subs(C1=Ceet[1],C2=Ceet[2],Y);
|
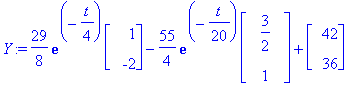
![y12 := vector([29/8*exp(-1/4*t)-165/8*exp(-1/20*t)+42, -29/4*exp(-1/4*t)-55/4*exp(-1/20*t)+36])](images/L12maple17.gif)
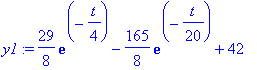
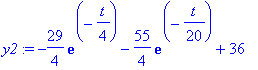
| > |
plot([y1,y2],t=0..100);
|
![[Maple Plot]](images/L12maple20.gif)
| > |
<diff(y1,t),diff(y2,t)>;
|
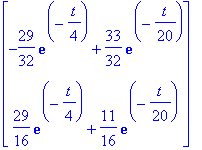
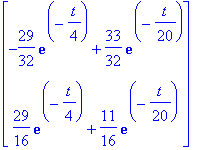
Kävihän se tarkistus toki näin!
2x2-systeemejä, faasitasoja
Katsotaan ensin, mikä on "aikatason" ja faasitason suhde ja mikä on vastaava Maple-syntaksi.
Merkitään havainnollisuuden vuoksi faasitason pisteitä (x(t) , y(t)).
Olk.
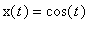 ,
,
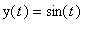 .
.
| > |
plot([x,y],t=0..2*Pi,title="Aikakuva");
|
![[Maple Plot]](images/L12maple25.gif)
| > |
plot([x,y,t=0..2*Pi],title="Faasikuva");
|
![[Maple Plot]](images/L12maple26.gif)
Esim. 1 (KRE s. 163)
| > |
restart: with(LinearAlgebra): with(linalg): with(plots):
|
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
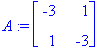
| > |
(lambda,ov):=Eigenvectors(A);
|
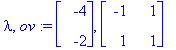
| > |
x1:=ov[1..-1,1]; x2:=ov[1..-1,2];
|
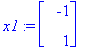
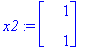
| > |
Y:=C1*exp(lambda[1]*t)*x1+C2*exp(lambda[2]*t)*x2;
|
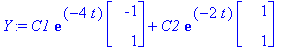
| > |
C1:=1: C2:=.5: plot([Y[1],Y[2]],t=0..2,title="Ratkaisufunktiot y1(t)ja y2(t) aikakuvassa",color=[red,blue]);
|
![[Maple Plot]](images/L12maple32.gif)
Faasikuvan piirtämistä ajatellen kannattaa katsoa taas ominaisvektorikantaa, Sekä käsin, että Maplella on helpompaa, jos otetaan käyräparametriksi
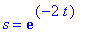
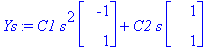
![YY := vector([-C1*s^2+C2*s, C1*s^2+C2*s])](images/L12maple35.gif)
| > |
C1:=arvo1: C2:=arvo2: 'plot'([YY[1],YY[2],s=a..b]); # Huomaa param. piirron syntaksi!
|
![plot([-arvo1*s^2+arvo2*s, arvo1*s^2+arvo2*s, s = a .. b])](images/L12maple36.gif)
| > |
C1:=-2: C2:=1: plot([YY[1],YY[2],s=0..1]);kuva1:=%:
|
![[Maple Plot]](images/L12maple37.gif)
| > |
C1:=2: C2:=-1: kuva2:=plot([YY[1],YY[2],s=0..1]):
|
![[Maple Plot]](images/L12maple38.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],s=0..1],C2=-2..2),C1=-2..2);
|
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/L12maple39.gif)
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/L12maple40.gif)
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/L12maple41.gif)
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/L12maple42.gif)
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/L12maple43.gif)
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/L12maple44.gif)
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/L12maple45.gif)
![[Maple Plot]](images/L12maple46.gif)
| > |
display(%,arrow([x1,x2]));
|
![[Maple Plot]](images/L12maple47.gif)
Warning, the name adjoint has been redefined
| > |
DEplot([D(y1)(t)=-3*y1(t)+y2(t),D(y2)(t)=y1(t)-3*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-4..4,y2=-4..4,color=grey);
|
![[Maple Plot]](images/L12maple48.gif)
| > |
display(kuva,%,title="Trajektoreita ja suuntakenttä");
|
![[Maple Plot]](images/L12maple49.gif)
2x2-faasitasotyypit
KRE:ssä on perusesimerkkejä ss. 164 - 168.
Käydään tässä EN:n sivujen mukaan ja käytetään EN-nimityksiä
[EN]: Eirola-Nevanlinna: Diff. yht. sys. L3-luentoja
Esim. 2.2 Lähde, ominaisarvot > 0
| > |
restart: with(LinearAlgebra): with(linalg): with(plots):
|
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
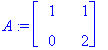
| > |
(lambda,ov):=Eigenvectors(A);
|
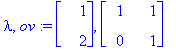
| > |
v1:=ov[1..-1,1]; v2:=ov[1..-1,2];
|
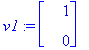
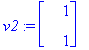
| > |
y:=t->C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
![y := proc (t) options operator, arrow; C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2 end proc](images/L12maple54.gif)
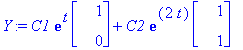
| > |
C1:=1: C2:=.5: plot([Y[1],Y[2]],t=0..2,title="Ratkaisufunktiot y1(t)ja y2(t) aikakuvassa",color=[red,blue]);
|
![[Maple Plot]](images/L12maple56.gif)
| > |
Ys:=map(eval,subs(t=log(s),y(t)));
|
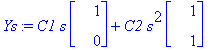
![YY := vector([C1*s+C2*s^2, C2*s^2])](images/L12maple58.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],s=0..4],C2=-2..2),C1=-2..2):
|
![[Maple Plot]](images/L12maple59.gif)
| > |
display(%,arrow([v1,v2]),view=[-5..5,-5..5]);
|
![[Maple Plot]](images/L12maple60.gif)
Warning, the name adjoint has been redefined
| > |
DEplot([D(y1)(t)=y1(t)+y2(t),D(y2)(t)=2*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey);
|
![[Maple Plot]](images/L12maple61.gif)
| > |
display(kuva,%,title="Lähde,lambda[1] > 0, lambda[2] > 0");
|
![[Maple Plot]](images/L12maple62.gif)
Esim. 2.3, Nielu, ominaisarvot < 0
Periaatteessa samanlainen kuin lähde edellä, mutta nyt ominaisarvot negatiiviset. Trajektirit virtaavat origoon.
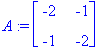
| > |
(lambda,ov):=Eigenvectors(A);
|
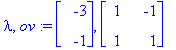
| > |
v1:=ov[1..-1,1]; v2:=ov[1..-1,2];
|
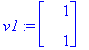
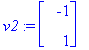
| > |
y:=t->C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
![y := proc (t) options operator, arrow; C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2 end proc](images/L12maple67.gif)
| > |
subs(t=log(s),y(t)): Ys:=eval(%); # Siirrytään logaritmiseen parametriin. Tämä ei ole välttämätöntä, mutta helpottaa erit. käsin piirtoa, myös Maple-piirrossa skaala pysyy paremmin hanskassa.
|
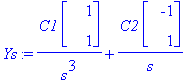
| > |
# 0 < s < 1, kun t > 0.
|
Lasketaan koordinaattimuodossa:
![YY := vector([C1/s^3-C2/s, C1/s^3+C2/s])](images/L12maple69.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],s=0..4],C2=-2..2),C1=-2..2):
|
![[Maple Plot]](images/L12maple70.gif)
| > |
display(%,arrow([v1,v2]),view=[-5..5,-5..5]);
|
![[Maple Plot]](images/L12maple71.gif)
| > |
display(kuva,DEplot([D(y1)(t)=-2*y1(t)-y2(t),D(y2)(t)=-y1(t)-2*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey),title="Nielu");
|
![[Maple Plot]](images/L12maple72.gif)
Nielu on vahvasti stabiili. Kaikki trajektorit lähestyvät O:a, kun t ->
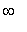 .
.
Esim 2.4 Satula, reaaliset, erimerkk.
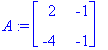
| > |
(lambda,ov):=Eigenvectors(A);
|
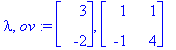
| > |
v1:=ov[1..-1,1]; v2:=ov[1..-1,2];
|
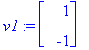
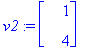
| > |
Y:=C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
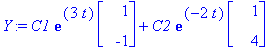
| > |
subs(t=log(s),Y);Ys:=eval(%);
|
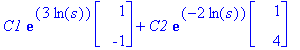
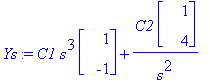
![YY := vector([C1*s^3+C2/s^2, -C1*s^3+4*C2/s^2])](images/L12maple81.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],s=0..4],C2=-2..2),C1=-2..2):
|
![[Maple Plot]](images/L12maple82.gif)
| > |
display(%,arrow([v1,v2]),view=[-5..5,-5..5]);
|
![[Maple Plot]](images/L12maple83.gif)
| > |
display(kuva,DEplot([D(y1)(t)=2*y1(t)-y2(t),D(y2)(t)=-4*y1(t)-y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey),title="Satula");
|
![[Maple Plot]](images/L12maple84.gif)
Epästabiili.
Osa trajektoreista -->
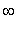 , lähdettiinpä miten läheltä O:a tahansa (erit. posit. ominaisarvoa vastaavan
, lähdettiinpä miten läheltä O:a tahansa (erit. posit. ominaisarvoa vastaavan
ominaisvektorin pisteistä).
Esim. 2.5, epästabiili fokus , kompleksiset, Re(
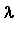 ) > 0
) > 0
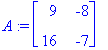
| > |
(lambda,ov):=Eigenvectors(A);
|
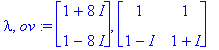
| > |
v1:=ov[1..-1,1]; v2:=ov[1..-1,2];
|
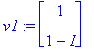
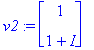
| > |
Y:=C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
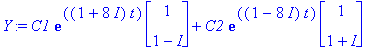
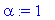
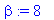
| > |
u:=map(Re,v1); v:=map(Im,v1);
|
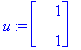
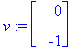
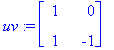
| > |
C:=<<cos(beta*t),-sin(beta*t)>|<sin(beta*t),cos(beta*t)>>;
|
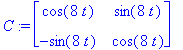
| > |
Y:=exp(alpha*t)*(uv.C.<C1,C2>); # Sulut laitettava näin, Maple ei täysin hallitse kertolaskujen liitännäisyyttä.
|
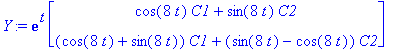
![YY := vector([exp(t)*(cos(8*t)*C1+sin(8*t)*C2), exp(t)*((cos(8*t)+sin(8*t))*C1+(sin(8*t)-cos(8*t))*C2)])](images/L12maple99.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],t=0..2],C2=-2..2),C1=-2..2):
|
![[Maple Plot]](images/L12maple100.gif)
| > |
display(%,arrow([u,v]),view=[-5..5,-5..5]);
|
![[Maple Plot]](images/L12maple101.gif)
| > |
display(kuva,DEplot([D(y1)(t)=9*y1(t)-8*y2(t),D(y2)(t)=16*y1(t)-7*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey),title="Epästabiili fokus");
|
![[Maple Plot]](images/L12maple102.gif)
Esim. 3.0 Degeneroitununut lähde (KRE s. 168)
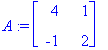
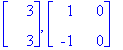
| > |
expA:=t->exp(3*t)*<<1+t,-t>|<t,1-t>>;
|
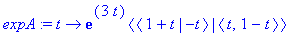
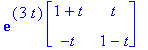
| > |
exponential(A,t); # Tarkistus.
|
![matrix([[exp(3*t)+t*exp(3*t), t*exp(3*t)], [-t*exp(3*t), exp(3*t)-t*exp(3*t)]])](images/L12maple107.gif)
| > |
Y:=exp(3*t)*((expA(t)/exp(3*t)).<C1,C2>);
|
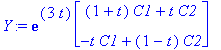
Jälleen piti temppuilla, koska kertolaskun liitännäisyys ei ole ihan hallinnassa.
![YY := vector([exp(3*t)*((1+t)*C1+t*C2), exp(3*t)*(-t*C1+(1-t)*C2)])](images/L12maple109.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],t=-2..2],C2=-2..2),C1=-2..2):
|
| > |
display(plot([parvi]),arrow(<-1,1>),view=[-5..5,-5..5],title="Degeneroitunut lähde");
|
![[Maple Plot]](images/L12maple110.gif)
Vaihtoehtoisia tapoja piirtoon (Maple-teknikkaa)
Olemme harrastaneet grafiikka-arvoisia funktioita, kuten traje edellä diffrenssiyhtälöissä.
Tässäkin voisimme tehdä vastaavasti:
| > |
dystraje:=(C1,C2)->plot([-C1*s^2+C2*s,C1*s^2+C2*s,s=0..1]):
|
| > |
display(dystraje(1,1));
|
![[Maple Plot]](images/L12maple111.gif)
| > |
display(seq(seq(dystraje(C1,C2),C2=-2..2),C1=-1..1));
|
![[Maple Plot]](images/L12maple112.gif)
Kannattaisi kirjoittaa sellainen, joka laskee ja piirtää trajektorin annetusta alkupisteestä lähtien.
Esim. 1
Tässä laskemme analyyttisen ratkaisun, mutta teemme kaiken piirtämisen DEplot:lla. Se on karkeampi tapa, mutta
hyvä demota sitäkin. Kuvaan voitaisiin lisätä dystraje:lla laskettuja trajektoreita.
| > |
restart: with(LinearAlgebra):
|
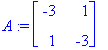
| > |
(lambda,ov):=Eigenvectors(A);
|
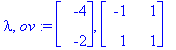
| > |
x1:=ov[1..-1,1]; x2:=ov[1..-1,2];
|
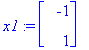
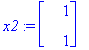
| > |
Y:=C1*exp(lambda[1]*t)*x1+C2*exp(lambda[2]*t)*x2;
|
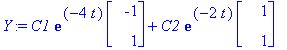
| > |
Y:=convert(evalm(%),list);
|
![Y := [-C1*exp(-4*t)+C2*exp(-2*t), C1*exp(-4*t)+C2*exp(-2*t)]](images/L12maple118.gif)
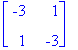
| > |
alkuarvolista:=[[y1(0)=2,y2(0)=4],[y1(0)=1,y2(0)=1],[y1(0)=-1,y2(0)=1],[y1(0)=1,y2(0)=-1],[y1(0)=-8,y2(0)=4],[y1(0)=-4.04,y2(0)= 7.49]]:
|
| > |
DEplot([D(y1)(t)=-3*y1(t)+y2(t),D(y2)(t)=y1(t)-3*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-10..10,y2=-10..10,alkuarvolista,stepsize=.05);
|
![[Maple Plot]](images/L12maple120.gif)
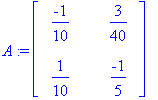
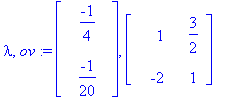
![x := [Vector(%id = 20022384), Vector(%id = 20022944)]](images/L12maple3.gif)
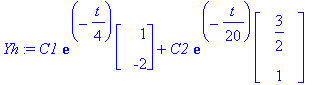
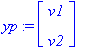
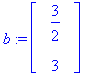
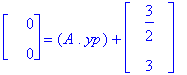
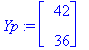
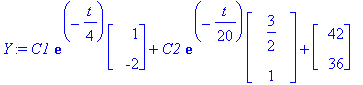
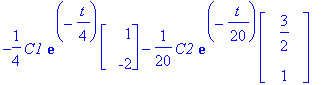
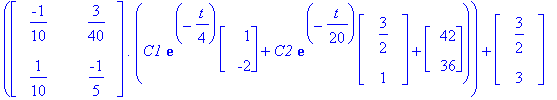
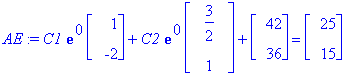
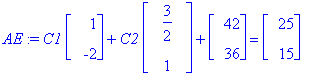
![]()
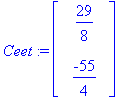
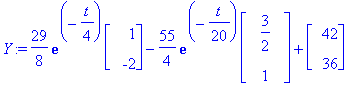
![y12 := vector([29/8*exp(-1/4*t)-165/8*exp(-1/20*t)+42, -29/4*exp(-1/4*t)-55/4*exp(-1/20*t)+36])](images/L12maple17.gif)
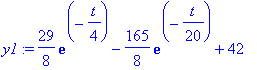
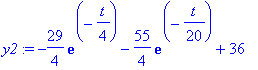
![[Maple Plot]](images/L12maple20.gif)
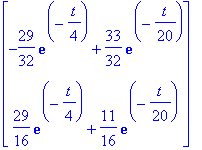
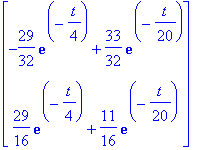
![[Maple Plot]](images/L12maple25.gif)
![[Maple Plot]](images/L12maple26.gif)
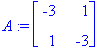
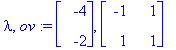
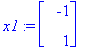
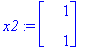
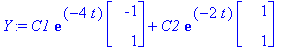
![[Maple Plot]](images/L12maple32.gif)
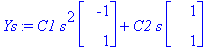
![[Maple Plot]](images/L12maple37.gif)
![[Maple Plot]](images/L12maple38.gif)
![[Maple Plot]](images/L12maple46.gif)
![[Maple Plot]](images/L12maple47.gif)
![[Maple Plot]](images/L12maple48.gif)
![[Maple Plot]](images/L12maple49.gif)
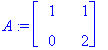
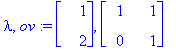
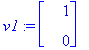
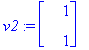
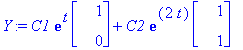
![[Maple Plot]](images/L12maple56.gif)
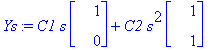
![[Maple Plot]](images/L12maple59.gif)
![[Maple Plot]](images/L12maple60.gif)
![[Maple Plot]](images/L12maple61.gif)
![[Maple Plot]](images/L12maple62.gif)
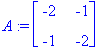
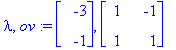
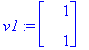
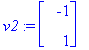
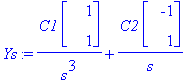
![YY := vector([C1/s^3-C2/s, C1/s^3+C2/s])](images/L12maple69.gif)
![[Maple Plot]](images/L12maple70.gif)
![[Maple Plot]](images/L12maple71.gif)
![[Maple Plot]](images/L12maple72.gif)
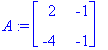
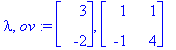
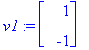
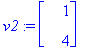
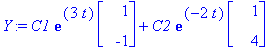
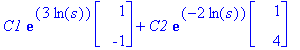
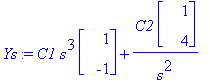
![YY := vector([C1*s^3+C2/s^2, -C1*s^3+4*C2/s^2])](images/L12maple81.gif)
![[Maple Plot]](images/L12maple82.gif)
![[Maple Plot]](images/L12maple83.gif)
![[Maple Plot]](images/L12maple84.gif)
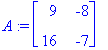
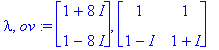
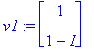
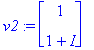
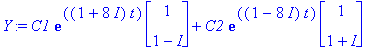
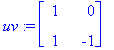
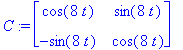
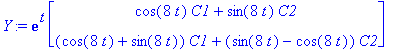
![[Maple Plot]](images/L12maple100.gif)
![[Maple Plot]](images/L12maple101.gif)
![[Maple Plot]](images/L12maple102.gif)
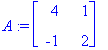
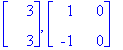
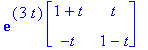
![matrix([[exp(3*t)+t*exp(3*t), t*exp(3*t)], [-t*exp(3*t), exp(3*t)-t*exp(3*t)]])](images/L12maple107.gif)
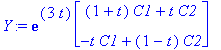
![[Maple Plot]](images/L12maple110.gif)
![[Maple Plot]](images/L12maple111.gif)
![[Maple Plot]](images/L12maple112.gif)
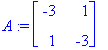
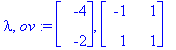
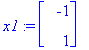
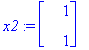
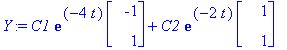
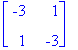
![[Maple Plot]](images/L12maple120.gif)