Värähtelyliike L11maple.mws
ti 29.10.02 HA
Kirjallisuus:
KRE 2.2 s. 72 -> 2. kl. vakiokertoimiset, (2. asteen yhtälön juuret => 3 eri tapausta)
Mallinnusta: (Sama uudelleen fysikaalisin tulkinnoin, mekaaniset värähtelyt, sähkövärähtelyt)
2.5 s. 83 -> Vapaat värähtelyt (Free oscillations)
2.11 s. 111 -> Pakotetut värähtelyt (Forced oscillations)
1. Vapaa vaimentamaton , eli harmoninen värähtely (HY)
Warning, the name changecoords has been redefined
| > |
dyht:=diff(y(t),t,t)+w0^2*y(t)=0;
|
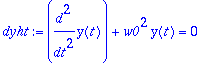
| > |
w0yht:=w0=sqrt(k/m): # T:=2*Pi/w0: f0:=1/T: # assign(w0yht): antaa ko. arvon w0:lle.
|
Tiedämme entuudestaan ja näemme suoraan yhtälöstä, että alla oleva on yleinen ratkaisu. Antaa nyt Maplenkin vielä laskea:
| > |
y:=A*cos(w0*t)+B*sin(w0*t);
|
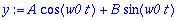
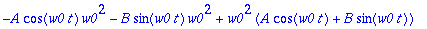

Alkuehdot vaikkapa: y(0)=1, y'(0)=0.
| > |
AE:={subs(t=0,y)=1,subs(t=0,diff(y,t))=0};
|
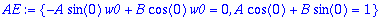
| > |
vakiot:=solve(AE,{A,B});
|
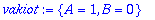
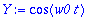
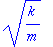
| > |
k:=2: m:=1: w0; Y; # k on jousivakio, m on massa.
|
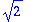
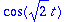
![[Maple Plot]](images/L11maple11.gif)
Tämän mallin pohjalta on helppo tehdä erilaisia tapauksia. Muutellaan vain parametrejä
k ja m sekä alkuehtoja.
Amplitudi ja vaihekulma nähdään muodosta
,
![y = C*cos(omega[0]*t-delta)](images/L11maple12.gif) .
.
| > |
C:=sqrt(A^2+B^2); delta:=arctan(B,A);
|
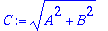

"Kiintoisammat" alkuehdot, kuten y(0)=1, y'(0)=2
.
| > |
AE:={subs(t=0,y)=1,subs(t=0,diff(y,t))=2};
|
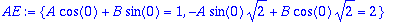
| > |
vakiot:=solve(AE,{A,B});
|
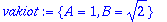
| > |
assign(vakiot); # Hiukan vaarallista, mutta tässä aika kätevää.
|
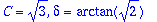
| > |
plot(C*cos(w0*t-delta),t=0..2*2*Pi/w0,title="Kaksi jaksoa");
|
![[Maple Plot]](images/L11maple18.gif)
1.1. Vapaa vaimentamaton, esimerkki
Esim.
10 gramman massa venyttää jousta
![s[0]](images/L11maple19.gif) = 2 cm.
Massaa vedetään alaspäin 2 cm tasapainoasemastaan
= 2 cm.
Massaa vedetään alaspäin 2 cm tasapainoasemastaan
ja annetaan sille alkunytkäys 1 m/s ylöspäin.
Määritä massan sijainti ajan funktiona. Määritä jakso, amplitudi ja vaihekulma.
Warning, the name changecoords has been redefined
| > |
dyht:=diff(y(t),t,t)+(k/m)*y(t)=0;
|
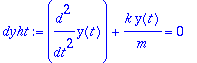
| > |
k*s0=m*g; k:=solve(%,k);
|
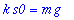
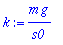

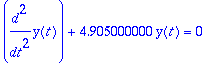
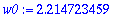
Yl- ratkaisu:
| > |
y:=A*cos(w0*t)+B*sin(w0*t);
|
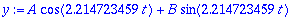
| > |
Y:=C*cos(w0*t-delta); # Ratkaisu muodossa "amplitudi ja vaihekulma".
|
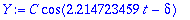
| > |
C:=sqrt(A^2+B^2); delta:=arctan(B,A);
|
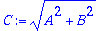

| > |
yf:=unapply(y,t); # Määritellään lauseke funktioksi, AE-yhtälöt helpompi muodostaa.
|
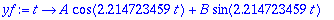
| > |
AE1:={yf(0)=1,D(yf)(0)=0}: solve(AE1,{A,B}): y1:=subs(%,y);
|
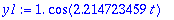
| > |
AE2:={yf(0)=1,D(yf)(0)=1}: solve(AE2,{A,B}): y2:=subs(%,y);
|
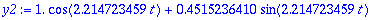
| > |
AE3:={yf(0)=1,D(yf)(0)=-1}: solve(AE3,{A,B}): y3:=subs(%,y);
|
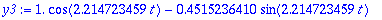
| > |
T:=2*Pi/w0; w0:=sqrt(k/m): T;
|
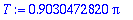
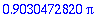
| > |
plot([y1,y2,y3],t=0..2*T,color=[red,green,blue],title="Punainen:y'(0)=0,vihreä: y'(0)=1, sininen: y'(0)=-1");
|
![[Maple Plot]](images/L11maple36.gif)
Sinisellä ja vihreällä on sama amplitudi, punaisella pienempi (minimaalinen tällä alkupoikkeutuksella).
Lasketaanpa vielä:
| > |
solve(AE1,{A,B}); C1:=subs(%,sqrt(A^2+B^2)); delta[1]:=subs(%%,arctan(B,A));eval(%);
|
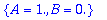
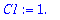
![delta[1] := arctan(0.,1.)](images/L11maple39.gif)

| > |
solve(AE2,{A,B}); C2:=subs(%,sqrt(A^2+B^2)); delta[2]:=subs(%%,arctan(B,A));eval(%);
|
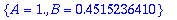

![delta[2] := arctan(.4515236410,1.)](images/L11maple43.gif)

| > |
solve(AE3,{A,B}); C3:=subs(%,sqrt(A^2+B^2)); delta[3]:=subs(%%,arctan(B,A));eval(%);
|
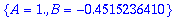

![delta[3] := arctan(-.4515236410,1.)](images/L11maple47.gif)

2. Vaimennettu (vapaa) värähtely (HY)
Systeemissä on yleensä vastusta: kitkaa, ilman tai nesteen vastusta ym. Siinä voi myös olla mekaaninen iskunvaimentaja
"shock absorber", "dashpot".
Jos liike ei ole kovin nopeaa, hyvä approksimaatio saadaan olettamalla vastusvoima verrannolliseksi nopeuteen.
Vastusvoima on tietysti liikkeen suunnalle vastakkainen
:
| > |
![F[v] = -c*diff(y(t),t)](images/L11maple49.gif)
|
Warning, the name changecoords has been redefined
Liikeyhtälö saa yleisen muodon:
| > |
m*diff(y(t),t,t)+c*diff(y(t),t)+k*y(t)=0;
|
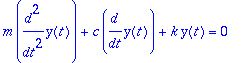
Yrite
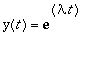 johtaa karakteristiseen yhtälöön
(kuten jo aiemmin todettiin):
johtaa karakteristiseen yhtälöön
(kuten jo aiemmin todettiin):
| > |
karpol:=lambda^2+c/m*lambda+k/m;
|
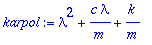
| > |
Lambda:=solve(karpol=0,lambda);
|
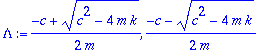
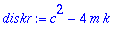
Diskriminantin merkkikäytös määrää tapaukset I, II, III
.
Ylivaimennus, diskr > 0
Kaksi erillistä reaalijuurta
![lambda[1]](images/L11maple55.gif) ja
ja
![lambda[2]](images/L11maple56.gif) , yleinen ratkaisu:
, yleinen ratkaisu:
| > |
![y := C[1]*exp(lambda[1]*t)+C[2]*exp(lambda[2]*t)](images/L11maple57.gif)
|
Kriittinen vaimennus, diskr = 0
Reaalinen kaksoisjuuri
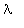 . Yleinen ratkaisu:
. Yleinen ratkaisu:
| > |
![y := (C[1]+C[2]*t)*exp(lambda*t)](images/L11maple59.gif)
|
Alivaimennus, diskr < 0
Kompleksikonjugaattijuuret
![lambda[1] = alpha+I*beta](images/L11maple60.gif) ,
,
![lambda[2] = alpha-I*beta](images/L11maple61.gif) . Yleinen ratkaisu:
. Yleinen ratkaisu:
| > |
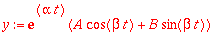
|
2.1. Esimerkkejä vapaasta vaimennetusta liikkeestä.
Seuraavissa 3 perustapausta.
Warning, the name changecoords has been redefined
| > |
dyht:=m*diff(y(t),t,t)+c*diff(y(t),t)+k*y(t)=0;
|
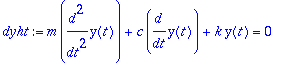
| > |
karyht:=m*lambda^2+c*lambda+k=0;diskr:=c^2-4*m*k;
|
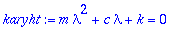
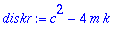
Pidetään m ja k samoina ja muutellaan vaimennuskerrointa c .
1. Ylivaimennus
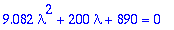
| > |
Lambda:=solve(karyht,lambda);
|
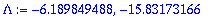
| > |
y:=C1*exp(Lambda[1]*t)+C2*exp(Lambda[2]*t);
|
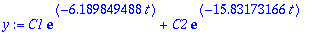
AE:
y(0)=0.15, y'(0)=0
.
| > |
AE:={subs(t=0,y)=0.15,subs(t=0,diff(y,t))=0};
|
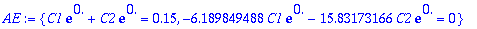
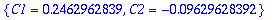
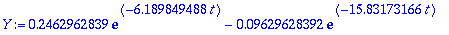
![[Maple Plot]](images/L11maple72.gif)
2. Kriittinen vaimennus

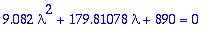
| > |
Lambda:=solve(karyht,lambda);
|
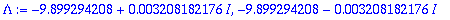
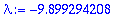
| > |
y:=(C1+C2*t)*exp(lambda*t);
|
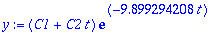
Kriittinen vaimennus on tietysti ideaalitapaus, käytännön laskuissa tulee yleensä pieni imag. termi tai sitten pieni ero reaalisten lambdojen välillä.
Tässä saadaan hyvä approksimaatio jättämällä pienet imaginaariosat pois.
Alkuehdot: y(0)=0.15, y'(0)=-0.2
| > |
AE:=subs(t=0,y)=0.15,subs(t=0,diff(y,t))=-1.8;
|
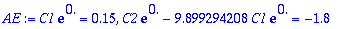
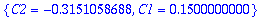
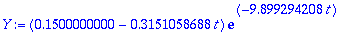
| > |
plot(Y,t=0..5,view=[0.3..1,-0.002..0.002]);
|
![[Maple Plot]](images/L11maple81.gif)
3. Alivaimennus
| > |
karyht;Lambda:=solve(karyht,lambda);
|
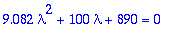
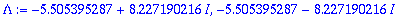
| > |
lambda:=Lambda[1]:alpha:=Re(lambda);w1:=abs(Im(lambda));
|
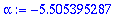
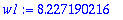
w1 on KRE:n omega*
| > |
y:=exp(alpha*t)*(A*cos(w1*t)+B*sin(w1*t));
|
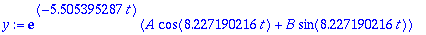
| > |
AE:=subs(t=0,y)=0.15,subs(t=0,diff(y,t))=0;
|
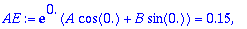
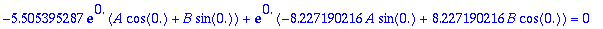
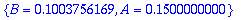
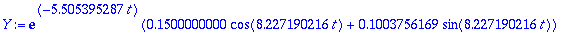
| > |
plots[display](array([[plot(Y,t=0..4)],[plot(Y,t=0.5..3)],[plot(Y,t=1..3)]]));
|
![[Maple Plot]](images/L11maple91.gif)
| > |
plot(Y,t=0..4,view=[0..4,-0.02..0.02],axes=boxed);
|
![[Maple Plot]](images/L11maple92.gif)
3. Pakotettu värähtely, (EHY)
Warning, the name changecoords has been redefined
| > |
dyht:=m*diff(x(t),t,t)+c*diff(x(t),t)+k*x(t)=F0*cos(w*t);
|
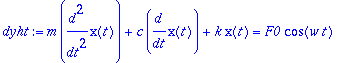
Käytetään
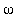 :n sijasta
:n sijasta
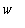 :tä, koska omega0 ei ole hauska.
:tä, koska omega0 ei ole hauska.
Tapaus 1. Vaimentamaton pakkovärähtely
Warning, the name changecoords has been redefined
| > |
diffy:=diff(y(t),t,t)+w0^2*y(t)=F0/m*cos(omega*t);
|
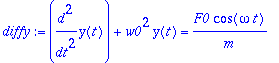
| > |
yp:=a*cos(omega*t)+b*sin(omega*t);
|
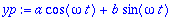
| > |
yht:=eval(subs(y(t)=yp,diffy));
|
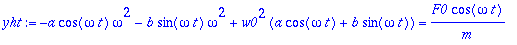
| > |
yht:={map(coeff,yht,cos(omega*t)),map(coeff,yht,sin(omega*t))};
|
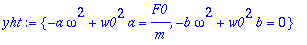
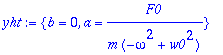
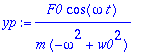
Tämä siis pätee, jos
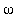 # w0.
# w0.
Ei resonanssi , eli
![omega <> omega[0]](images/L11maple103.gif)
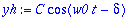
| > |
w0=sqrt(k/m); # Emme tee sijoitusta, muistutamme vain
|
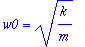
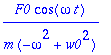
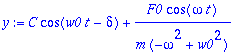
Mitä tapahtuu, kun
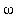 -> w0 ?
-> w0 ?
Resonanssi,
![omega = omega[0]](images/L11maple109.gif)
Nyt äskeinen yrite ei toimi, sillä se toteuttaa (HY):n, eikä siten millään voi toteuttaa EHY:ä.
Warning, the name changecoords has been redefined
Pulmatilanteissa t:llä kertominen on tuottanut hyvän yritteen, Niinpä kannattaa ainakin yrittää: (KRE: "mofifcation rules", kohta 2.9.)
| > |
yp:=t*(a*cos(w0*t)+b*sin(w0*t));
|
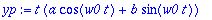
| > |
yhtalo:=simplify(diff(yp,t,t)+w0^2*yp)=F0*cos(w0*t)/m;
|
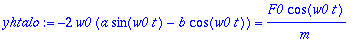
| > |
map(coeff,yhtalo,sin(w0*t)),map(coeff,yhtalo,cos(w0*t));
|
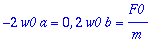
| > |
solve({%},{a,b});assign(%):
|
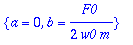
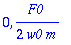
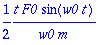
![[Maple Plot]](images/L11maple116.gif)
Huojunta, beats
Lue KRE ss. 114 - 115. Tästä ehkä harj. teht.
Tapaus 2. Vaimennettu pakkovärähtely
Ol: c > 0,
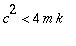 .
.
Warning, the name changecoords has been redefined
| > |
dyht:=m*diff(y(t),t,t)+c*diff(y(t),t)+k*y(t)=F0*cos(omega*t);
|
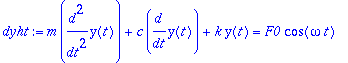
EHY-yrite:
| > |
yp:=a*cos(omega*t)+b*sin(omega*t);
|
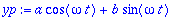
| > |
yht:=eval(subs(y(t)=yp,dyht));
|
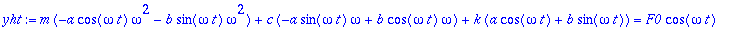
| > |
yht:={map(coeff,yht,cos(omega*t)),map(coeff,yht,sin(omega*t))};
|
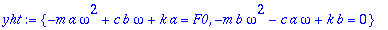
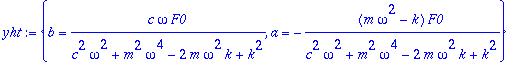
Lausekkeita voidaan vähän sieventää ottamalla
![omega[0]^2 = k/m](images/L11maple123.gif) käyttöön (vrt. KRE kaavat (5) s. 113.
käyttöön (vrt. KRE kaavat (5) s. 113.
Tarvitsemme yleisiä kaavoja etupäässä siihen tietoon, että kertoimet a ja b voidaan aina määrätä. (Olipa
![omega = omega[0]](images/L11maple124.gif) tai ei.).
tai ei.).
Yleisistä kaavoista saadaan myös resonanssityylinen kaava asettamalla vain
![omega = omega[0]](images/L11maple125.gif) . Toisaalta Maple tekee
. Toisaalta Maple tekee
johtamisen puolestamme, kuten edelläkin.
Warning, the name changecoords has been redefined
| > |
dyht:=diff(y(t),t,t)+c/m*diff(y(t),t)+w0^2*y(t)=F0/m*cos(w0*t);
|
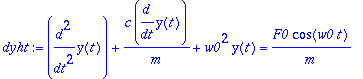
EHY-yrite:
| > |
yp:=a*cos(w0*t)+b*sin(w0*t);
|
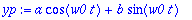
| > |
yht:=eval(subs(y(t)=yp,dyht));
|
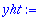
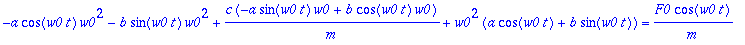
| > |
yht:={map(coeff,yht,cos(w0*t)),map(coeff,yht,sin(w0*t))};
|
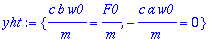
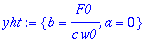
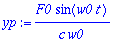
Jos vaimennusvakio on pieni, niin amplitudi on suuri, mutta pysyy kuitenkin äärellisenä, kun kerran vaimennusta on (c > 0).
Kun c --> 0, niin amplitudi kasvaa rajatta, jolloin lähestytään vaimentamatonta resonanssitapausta.
Esim.
Warning, the name changecoords has been redefined
| > |
EHY:=m*diff(y(t),t,t)+c*diff(y(t),t)+k*y(t)=10*cos(omega*t);
|
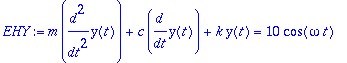
| > |
HY:=lhs(EHY)=0:HY:=subs(m=1,c=4,k=24,HY);
|
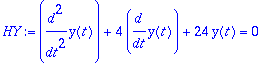
| > |
lambda^2+4*lambda+24=0; solve(%,lambda);
|
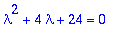
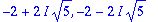
Siis kompleksijuuret (alivaimennus), joten värähtelyä on luvassa.
Tästä nähdään heti HY:n yleinen. Demonstroidaan tässä kuitenkin annetaan Maplen yleistä diffyht.ratkaisijaa
dsolve
:a.
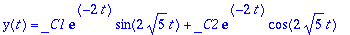
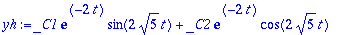
EHY-yrite:
| > |
yp:=a*cos(omega*t)+b*sin(omega*t);
|
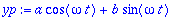
| > |
yht:=eval(subs(y(t)=yp,EHY));
|
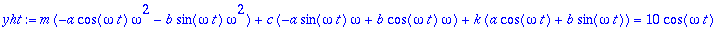
| > |
yht:={map(coeff,yht,cos(omega*t)),map(coeff,yht,sin(omega*t))};
|
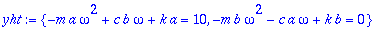
| > |
yht:=subs(m=1,c=4,k=24,yht);
|
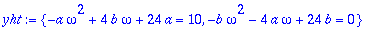
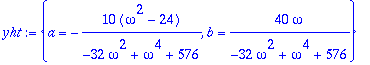
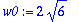
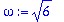
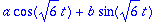
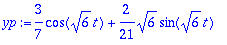
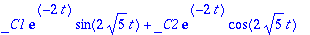
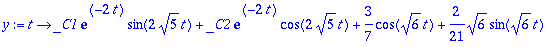
| > |
AE:={y(0)=0.15,D(y)(0)=0};
|
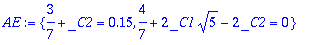
| > |
kertoimet:=solve(AE,{_C1,_C2});
|
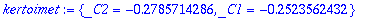
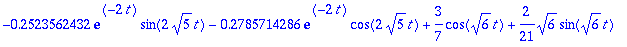
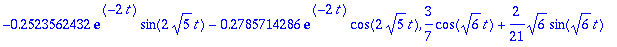
| > |
plot([yh,yp,yh+yp],t=0..8,color=[red,green,blue],title="Punainen transientti,vihreä: tasapainotila, sininen: yh+yp");
|
![[Maple Plot]](images/L11maple154.gif)
| > |
plot([yh+yp],t=0..8,color=[blue],title="Koko ratkaisu yh+yp");
|
![[Maple Plot]](images/L11maple155.gif)
-
Punainen
![y[h]](images/L11maple156.gif) edustaa alkuehdoista riippuvaa
"transienttia"
osaa,joka kestää vain hetken ja sammuu pian pois.
edustaa alkuehdoista riippuvaa
"transienttia"
osaa,joka kestää vain hetken ja sammuu pian pois.
-
Vihreä y[p] edustaa pysyvää, "
steady state
", (dynaamista)
tasapainotilaratkaisua
, joka jää, kun aikaa kuluu (kun transientti on
kuollut pois (käytännöllisesti katsoen).
-
Sininen on koko ratkaisu, joka selvästikään ei juuri erotu vihreästä, kun aikaa kuluu.
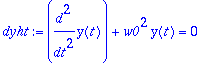
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Maple Plot]](images/L11maple11.gif)
![]() .
.
![]()
![]()
![]()
![]()
![]()
![[Maple Plot]](images/L11maple18.gif)
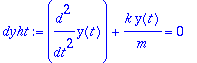
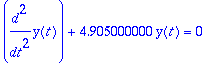
![[Maple Plot]](images/L11maple36.gif)
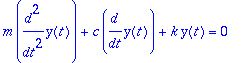
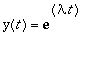 johtaa karakteristiseen yhtälöön
(kuten jo aiemmin todettiin):
johtaa karakteristiseen yhtälöön
(kuten jo aiemmin todettiin):
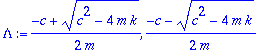
![[Maple Plot]](images/L11maple72.gif)
![[Maple Plot]](images/L11maple81.gif)
![[Maple Plot]](images/L11maple91.gif)
![[Maple Plot]](images/L11maple92.gif)
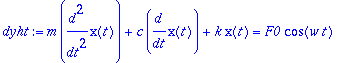
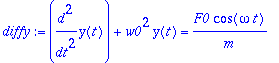
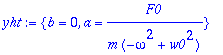
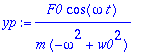
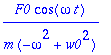
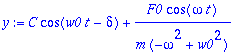
![[Maple Plot]](images/L11maple116.gif)
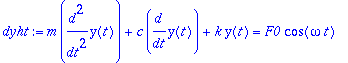
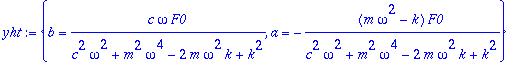
![omega[0]^2 = k/m](images/L11maple123.gif) käyttöön (vrt. KRE kaavat (5) s. 113.
käyttöön (vrt. KRE kaavat (5) s. 113.
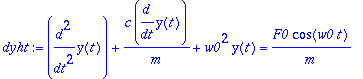
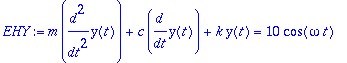
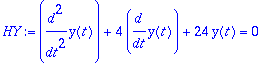
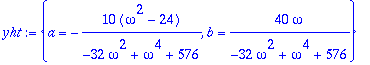
![[Maple Plot]](images/L11maple154.gif)
![[Maple Plot]](images/L11maple155.gif)