Alustukset
Warning, the name changecoords has been redefined
| > |
with(linalg):
with(LinearAlgebra):
|
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
| > |
alias(rref=ReducedRowEchelonForm): alias(ref=GaussianElimination): alias(Diag=DiagonalMatrix,Id=IdentityMatrix):
with(plots):
|
| > |
alias(Dot=DotProduct,Id=IdentityMatrix,T=Transpose):
|
Konjugointisäännöt
DotProduct:
ssa ova niin mutkikkaat ja monitahoiset, että on verrattomasti helpompaa määritellä
suosiolla oma
Sis:
-funktio sisätuloksi. (Lokalisointipuutteen takia käytetään "outoja" nimiä, kuten i_ )
| > |
Sis:=(u,v)->add(u[i_]*conjugate(v[i_]),i_=1..LinearAlgebra[Dimension](u)):
|
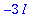
| > |
randV:=n->RandomVector(n,generator=rand(-1000..1000)/1000.);
|

| > |
randM:=(m,n)->RandomMatrix(m,n,generator=rand(-1000..1000)/1000.);
|
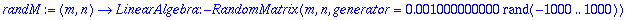
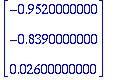
Ortogonaalisuus
Ortogonaalinen kanta
Esim: (a) Osoita, että vektorit
| > |
u1:=<3,1,1>; u2:=<-1,2,1>; u3:=<-1/2,-2,7/2>;
|
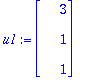
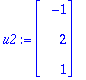
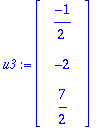
muodostavat OG kannan.
| > |
T(u1).u2;T(u1).u3;T(u2).u3;
|



M.O.T . Voidaan tehdä kootusti näin:
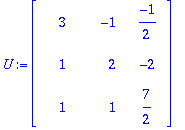
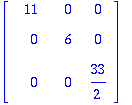
MOT (koska saimme diagonaalimatriisin).
Laske annetun vektorin
v
esitys tässä OG kannassa.
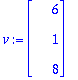
| > |
e1:=Normalize(u1,2):e2:=Normalize(u2,2):e3:=Normalize(u3,2):
|
| > |
vesitys:=Sis(v,e1)*'e1'+Sis(v,e2)*'e2'+Sis(v,e3)*'e3';
|
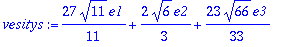
| > |
v=eval(vesitys); # Kaikkea muuta kuin vesitys!
|
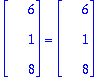
| > |
a1:=arrow(e1,color=red):a2:=arrow(e2,color=blue):a3:=arrow(e3,color=green): a:=arrow(v,shape=arrow,color=gray):
|
| > |
display(a1,a2,a3,a,scaling=constrained,axes=boxed);
|
![[Maple Plot]](images/L10maple17.gif)
Gram-Schmidt ortogonalisointi
Annnettu LRT vektorit v[1],...,v[m] sisätuloavaruudessa V.
Voidaan konstruoida ON vektorit e[1], ..., e[m], siten, että
sp(v[1],...,v[k]) = sp(e[1],...,e[k]) , k = 1 .. m
Konstruktion idea: Kts.
L10.html
Maple-lasku: harj6av.mws (kts. ip.)
Maplessa on toki valmiiksi ohjelmoituna:
| > |
w1 := <2,1,0,-1>:
w2 := <1,0,2,-1>:
w3 := <0,-2,1,0>:
orto := GramSchmidt([w1,w2,w3]);
|
![orto := [Vector(%id = 134769684), Vector(%id = 134770068), Vector(%id = 134771892)]](images/L10maple18.gif)
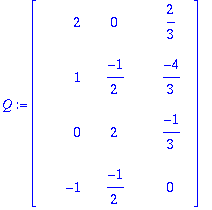
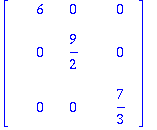
Kätevä tapa nähdä vektorien ortogonaalisuus.
Paras approksimaatio, ortog. proj
Esim
| > |
v:=<-1,-5,10>: u1:=<5,-2,1>: u2:=<1,2,-1>:
|
Määritä v:n paras approksimaatio aliavaruudessa
sp{u1,u2} .

| > |
e1:=Normalize(u1,2): e2:=Normalize(u2,2):
|
| > |
projv:=Sis(v,e1)*e1+Sis(v,e2)*e2;
|
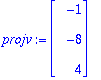
| > |
etaisyys:=Norm(v-projv,2);
|
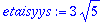
| > |
display(arrow(u1,color=blue,shape=arrow),arrow(u2,color=blue),arrow(v,color=red,shape=arrow),arrow(projv,color=green),arrow([[projv,v-projv]],color=gray),scaling=constrained,axes=boxed,title="Sininen aliavaruuden M kanta,punainen v, jonka vihreä projektio sinisellä aliavaruudella");
|
![[Maple Plot]](images/L10maple24.gif)
Vihreä on siis projektio (v*) ja harmaa on v - v*, joka on kohtisuorassa sinistä M:ää vastaan. (Harmaata merkittiin z:lla lauseen todistuksessa.)
QR-hajotelma
TE ss. 28 - 29
Lay ss. 405-407
Matriisihajotelma A=QR, missä Q ortog. ja R yläkolmio. (Yleensä A (m x n), m > n)
Algoritmi 1:
Oletetaan: A:n sarakkeet LRT. Ortonormeerataan GS:llä => Q. ortonormeerausprosessi tuottaa yläkölmiokertoimet, joista rakentuu R.
Algoritmi 2:
(Kts. TE) QR - hajotelma sadaan aikaan kertomalla ns. Householderin muunnoksilla vasemmalta.
Numeerisia huomioita:
Algoritmin 1 tulos kärsii peräkkäisten laskujen kuljettamista virheistä, joka aiheuttaa suurilla matriiseilla ortogonaalisuudem huononemista
helposti yli toleranssin erityisesti loppupään vektoreilla. Asiaa voidaan auttaa sopivasti järjestämällä.
Selvästi luotettavampi tulos saadaan jälkimmäisellä algoritmilla. Laskentatyön kaksinkertaistuminen on pieni haitta luotettavuuden ja tarkkuuden
liääntymisen rinnalla.
Esim:
| > |
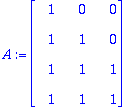
A:=<<1,1,1,1>|<0,1,1,1>|<0,0,1,1>>; # VarmastiLRTsarakkeet.
|
| > |
sarakkeet:=[seq(Column(A,j),j=1..3)];
|
![sarakkeet := [Vector(%id = 134622740), Vector(%id = 134663612), Vector(%id = 134912312)]](images/L10maple26.gif)
| > |
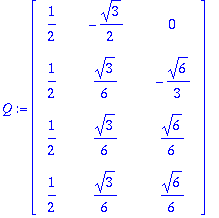
orto:=GramSchmidt(sarakkeet,normalized);
|
![orto := [Vector(%id = 135215956), Vector(%id = 135321200), Vector(%id = 135320740)]](images/L10maple27.gif)
| > |
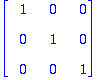
Transpose(Q).Q; # Tarkistetaan Q:n ortogonaalisuus (eli sarakkeiden ortonormaalisuus).
|
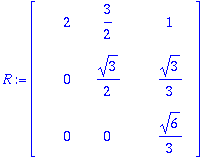
![Matrix(%id = 138358856) = Matrix(%id = 135740952), QjaR = [Matrix(%id = 135096592), Matrix(%id = 138385568)]](images/L10maple31.gif)
Tehdään sitten "oikella", numeerisesti laadukkaalla (toivottavasti) algoritmilla:
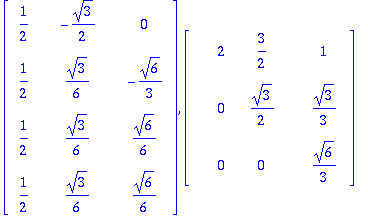
| > |
QRDecomposition(convert(A,float));
|

Paitsi PNS-tehtävissä, QR-hajotelmaa käytetään mm.
ominaisarvojen
ja -
vektoreiden numeerisessa
laskennassa.
TE: "QR on yhtä
tärkeä numeerisen matriisilaskennan työkalu
kuin Gaussin eliminointi."
![]()
![]()
![]()
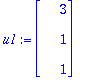
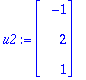
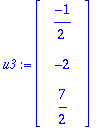


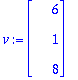
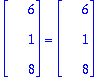
![[Maple Plot]](images/L10maple17.gif)
![orto := [Vector(%id = 134769684), Vector(%id = 134770068), Vector(%id = 134771892)]](images/L10maple18.gif)


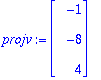
![[Maple Plot]](images/L10maple24.gif)

![sarakkeet := [Vector(%id = 134622740), Vector(%id = 134663612), Vector(%id = 134912312)]](images/L10maple26.gif)
![orto := [Vector(%id = 135215956), Vector(%id = 135321200), Vector(%id = 135320740)]](images/L10maple27.gif)



![Matrix(%id = 138358856) = Matrix(%id = 135740952), QjaR = [Matrix(%id = 135096592), Matrix(%id = 138385568)]](images/L10maple31.gif)

