Harj. 8 LV
pe 9.11.01 HA
1.
>
restart: with(inttrans): alias(L=laplace,IL=invlaplace,u=Heaviside):
%plots[setoptions](axes=boxed):
Warning, the name changecoords has been redefined
> dy:=diff(x(t),t,t)+2*diff(x(t),t)+x(t)=Dirac(t)-u(t-2*Pi);
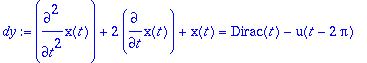
> AE:=x(0)=0,D(x)(0)=0;
![]()
> Ldy:=L(dy,t,s);Ldy:=subs(AE,Ldy);
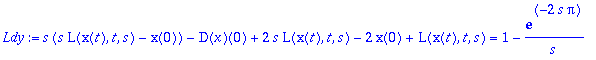
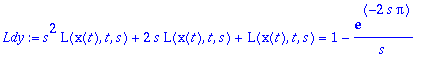
> X:=solve(Ldy,L(x(t),t,s));
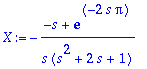
> nim:=denom(X):X1:=factor(s/nim);X2:=-1/factor(nim);
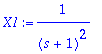
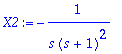
> x:=IL(X,s,t);
![]()
> plot(x,t=0..20);
![[Maple Plot]](images/harj8lv9.gif)
2.
>
restart: with(inttrans): alias(L=laplace,IL=invlaplace,u=Heaviside):
Warning, the name changecoords has been redefined
> Fa:=1/(s-a)^2;IL(Fa,s,t);
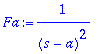
![]()
> Fb:=1/((s^2)*(s^2+omega^2));IL(Fb,s,t): simplify(%);
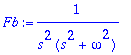
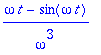
> convert(Fb,parfrac,s);
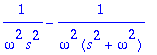
> Fc:=s/((s^2+omega^2)^2);IL(Fc,s,t): simplify(%);
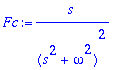
![]()
3.
4.
>
restart:alias(L=laplace, IL=invlaplace, u=Heaviside):
with(linalg):with(LinearAlgebra):with(inttrans):
A:=<<3 ,4>|<-2,1>>;
I2:=<<1,0>|<0,1>>;
A2:=Matrix(inverse(s*I2-A));
e:=map(IL,A2,s,t);
exponential(A,t);
g:=<<sin(t),-cos(t)>>;
G:=map(L,g,t,s);
X:=A2.G;
xt:=map(IL,X,s,t);
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
Warning, the name hilbert has been redefined
![A := _rtable[137010728]](images/harj8lv17.gif)
![I2 := _rtable[136427704]](images/harj8lv18.gif)
![A2 := _rtable[136551632]](images/harj8lv19.gif)
![e := _rtable[137208052]](images/harj8lv20.gif)
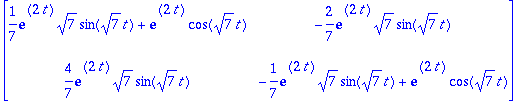
![g := _rtable[138410880]](images/harj8lv22.gif)
![G := _rtable[138399048]](images/harj8lv23.gif)
![X := _rtable[138261044]](images/harj8lv24.gif)
![xt := _rtable[136868048]](images/harj8lv25.gif)
5.
>
restart: with(inttrans): alias(L=laplace,IL=invlaplace,u=Heaviside):
plots[setoptions](axes=boxed):
Warning, the name changecoords has been redefined
Määritellään mieluummin symmetrisesti samalla tavoin kuin prujussa.
> delta[epsilon](t-a);
![]()
Tässä a=1, käytetään notaatiota (ja määritelmää)
>
d1:=(1/epsilon)*(u(t-1+epsilon/2)-u(t-1-epsilon/2));plot(subs(epsilon=0.2,d1),t=0..2);
Ld1:=1/(2*epsilon*s)*(exp(-s)*exp(epsilon*s/2)-exp(-epsilon*s/2));
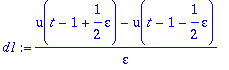
![[Maple Plot]](images/harj8lv28.gif)
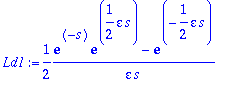
>
F:=1/(s*(s+1)*(s+2));
![]()
>
f:=unapply(IL(F,s,t),t);
![]()
>
y:=1/epsilon*(f(t-1+epsilon/2)*u(t-1+epsilon/2)-f(t-(1+epsilon/2))*u(t-(1+epsilon/2)));
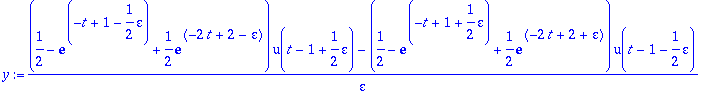
> y1:=subs(epsilon=1,y):y05:=subs(epsilon=0.5,y):y02:=subs(epsilon=0.2,y):y01:=subs(epsilon=0.1,y):y005:=subs(epsilon=0.05,y):
>
dy:=diff(x(t),t,t)+3*diff(x(t),t)+2*x(t)=Dirac(t-1);
AE:=x(0)=0,D(x)(0)=0;
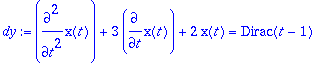
![]()
>
Ldy:=L(dy,t,s);Ldy:=subs(AE,Ldy);
![]()
![]()
>
>
X:=solve(Ldy,L(x(t),t,s));
x:=IL(X,s,t);
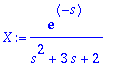
![]()
> plot(x,t=0..20);
![[Maple Plot]](images/harj8lv39.gif)
> plot([y1,y05,y02,y01,y005,x],t=0..4,color=[red,blue,black,green,cyan,gold]);
![[Maple Plot]](images/harj8lv40.gif)
> plot([y1,x],t=0..4,color=[blue,gold]);
![[Maple Plot]](images/harj8lv41.gif)
> plot([y02,x],t=0..4,color=[black,gold]);
![[Maple Plot]](images/harj8lv42.gif)
>