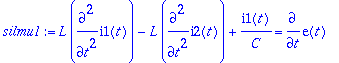
Harjoitus 8 AV

7.11.2001 Ha

1.

> restart: with(inttrans): alias(LL=laplace,IL=invlaplace,u=Heaviside): # Joudumme käyttämään LL-nimea, koska L on tässä tehtävässä varattu kelan induktanssille.

Warning, the name changecoords has been redefined

> silmu1:=L*diff(i1(t),t,t)-L*diff(i2(t),t,t)+i1(t)/C=diff(e(t),t); silmu2:=L*diff(i2(t),t)-L*diff(i1(t),t)+R*i2(t)=0;

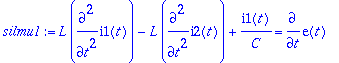
> L:=2;C:=50*10^(-6);R:=100;e:=t->50*sin(100*t);

> Ls1:=LL(silmu1,t,s);Ls2:=LL(silmu2,t,s);

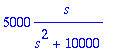
> AE:=i1(0)=0,i2(0)=0:

>

> Ls1:=subs(AE,Ls1);Ls2:=subs(AE,Ls2);

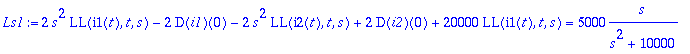
> solve({Ls1,Ls2},{LL(i1(t),t,s),LL(i2(t),t,s)});

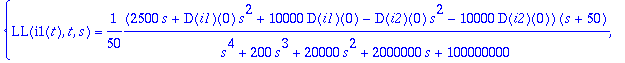
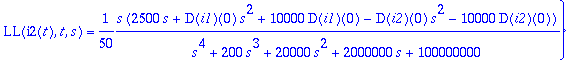
> I12:=subs(%,[LL(i1(t),t,s),LL(i2(t),t,s)]);

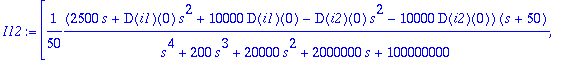
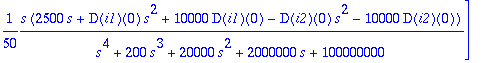
> I1:=I12[1]; I2:=I12[2];

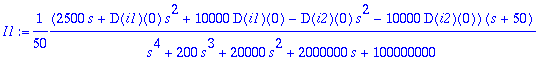
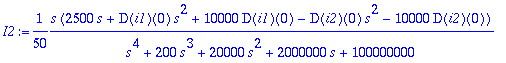
> I1:=convert(I1,parfrac,s);I2:=convert(I2,parfrac,s);

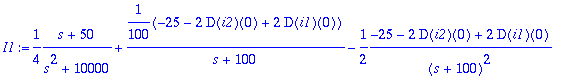
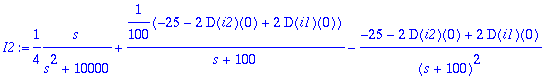
> ii1:=IL(I1,s,t);ii2:=IL(I2,s,t);

Tarvitsemme vielä lisäalkuehdon. Virtojen derivaatat eivät yleensä ole nollia. Koska kondensaattorin varaus = 0 alkuhetkellä, on

sen jännite =0, siten kelan jännitteen on oltava jännitelähteen jännite e(0), joka = 0.

Siispä 2(i1'-i2')=0 hetkellä t=0, joten i1'(0)=i2'(0).

Tämä riittääkin, kuten nähdään.

> ii1:=subs(D(i1)(0)=di0,D(i2)(0)=di0,ii1);ii2:=subs(D(i1)(0)=di0,D(i2)(0)=di0,ii2);

Tarkistus:

> (eval@subs)(i1(t)=ii1,i2(t)=ii2,silmu1);(eval@subs)(i1(t)=ii1,i2(t)=ii2,silmu2);

> (eval@subs)(t=0,ii2);

> plot([ii1,ii2],t=0..0.1);plot([ii1,ii2],t=0.1..0.4);plot([ii1,ii2],t=0.4..1);

Rakennetaan nyt yhtälöt suoraan integraalimuodosta:

> restart: with(inttrans): alias(LL=laplace,IL=invlaplace,u=Heaviside): # Joudumme käyttämään LL-nimea, koska L on tässä tehtävässä varattu kelan induktanssille.

Warning, the name changecoords has been redefined

> silmu1:=L*diff(i1(t),t)-L*diff(i2(t),t)+int(i1(tau),tau=0..t)/C=e(t); silmu2:=L*diff(i2(t),t)-L*diff(i1(t),t)+R*i2(t)=0;

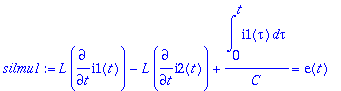
> L:=2;C:=50*10^(-6);R:=100;e:=t->50*sin(100*t);

> Ls1:=LL(silmu1,t,s);Ls2:=LL(silmu2,t,s);

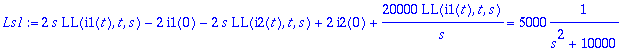
> AE:=i1(0)=0,i2(0)=0;

> Ls1:=subs(AE,Ls1);Ls2:=subs(AE,Ls2);

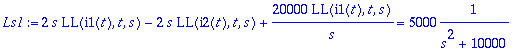
> solve({Ls1,Ls2},{LL(i1(t),t,s),LL(i2(t),t,s)});

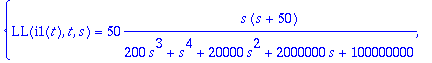
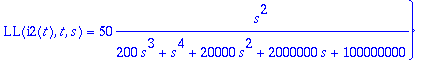
> I12:=subs(%,[LL(i1(t),t,s),LL(i2(t),t,s)]);

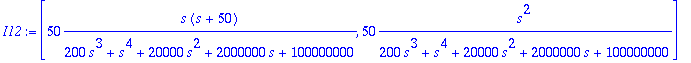
> I1:=I12[1]; I2:=I12[2];

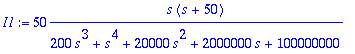
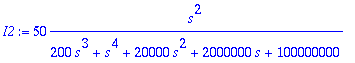
> I1:=convert(I1,parfrac,s);I2:=convert(I2,parfrac,s);

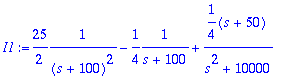
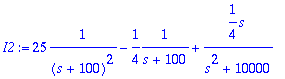
> ii1:=IL(I1,s,t);ii2:=IL(I2,s,t);

> ii1;ii2;

Tarkistus:

> (eval@subs)(i1(t)=ii1,i2(t)=ii2,silmu1);(eval@subs)(i1(t)=ii1,i2(t)=ii2,silmu2);

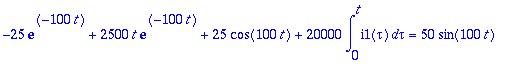
> -25*exp(-100*t)+2500*t*exp(-100*t)+25*cos(100*t)+20000*int(ii1,tau = 0 .. t) = 50*sin(100*t);map(eval,%);map(simplify,%);

>

Katsotaan alkuehdot:

> (eval@subs)(t=0,ii1);(eval@subs)(t=0,diff(ii1,t));(eval@subs)(t=0,ii2);(eval@subs)(t=0,diff(ii2,t));

Derivaatat alkuhetkellä ovat kaukana 0:sta, ne ovat 50, mutta samat, kuten edellä todettiin.

> plot([ii1,ii2],t=0..0.3);

2.

> restart: with(inttrans): alias(L=laplace,u=Heaviside):

Warning, the name changecoords has been redefined

a)

> plot(t*u(t),t=-1..1,axes=boxed);

> L(t*u(t),t,s);

b)

> f:=(t-1)*u(t-1):plot(f,t=0..2,axes=boxed);

> L(f,t,s);

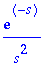
c)

> f:=4*u(t-1)*cos(t);

> plot(f,t=0..3*Pi,axes=boxed);

> L(f,t,s);

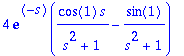
> Int(exp(-s*t)*4*cos(t),t=1..T): %=value(%);integr:=rhs(%);

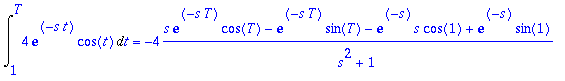
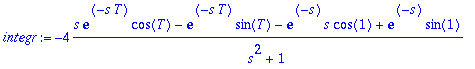
> assume(s>0): limit(integr,T=infinity);

>

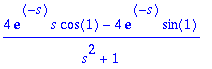
3.

> restart: with(inttrans): alias(L=laplace,IL=invlaplace,u=Heaviside):

Warning, the name changecoords has been redefined

a)

> F:=4/s*(exp(-2*s)-2*exp(-5*s));

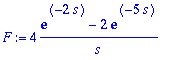
> IL(F,s,t);

b)

> G:=exp(-3*s)/(s-1)^3;

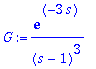
> IL(G,s,t);

> factor(%);

c)

> G:=s*exp(-2*s)/(s^2+Pi^2);

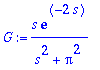
> IL(G,s,t);

> simplify(%);

4.

> restart: with(inttrans): alias(L=laplace,IL=invlaplace,u=Heaviside,esubs=eval@subs):

Warning, the name changecoords has been redefined

Ensin käsin laskien:

> F:=1/(s*(s+2));F:=convert(F,parfrac,s);

> f:=IL(F,s,t);

> G:=normal(F/s): G:=convert(%,parfrac,s);

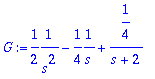
> g:=IL(G,s,t);

g saadaan myös integraalin muunnoskaavasta takaperin:

> int(subs(t=tau,f),tau=0..t);

> x:=f+u(t-1)*subs(t=t-1,g);

>

Tarkistus:

> diff(x,t,t)+2*diff(x,t);simplify(%);

> subs(t=0,x);eval(%);

> esubs(t=0,x);esubs(t=0,diff(x,t));

> diff(x,t);simplify(%);

> plot([u(t-1),x],t=0..4,axes=boxed);

>

5.

> restart: with(inttrans): alias(u=Heaviside): plots[setoptions](axes=boxed):

Warning, the name changecoords has been redefined

> fa:=u(t+1)-u(t);

> plot(fa,t=-2..1);

> fb:=u(t+2)-u(t+1)+u(t-1)-u(t-2);

> plot(fb,t=-3..3);

> CHI[1]:=u(t+2)-u(t); CHI[2]:=u(t)-u(t-3);

> fc:=(t+2)*CHI[1]+(2-2*t/3)*CHI[2];

> plot(fc,t=-3..4);

d)

> CHI:=u(t+2)-u(t-2);

> fd:=-1+u(t+2)+t*CHI/2+u(t-2);

> plot(fd,t=-3..3);

>

6.

> restart: with(inttrans): alias(u=Heaviside,L=laplace,IL=invlaplace): plots[setoptions](axes=boxed):

Warning, the name changecoords has been redefined

> g:=u(t)-2*u(t-1)+u(t-2);

> plot(g,t=-1..3);

> dy:=diff(y(t),t,t)+3*diff(y(t),t)+y(t)=g;AE:=y(0)=1,D(y)(0)=1;

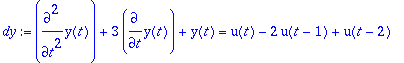
> Ldy:=subs(AE,L(dy,t,s));

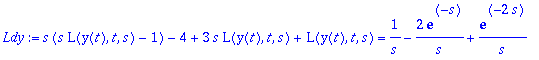
> Y:=solve(Ldy,L(y(t),t,s));

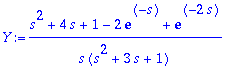
> nim:=denom(Y);oso:=-(-s^2-4*s-1+2*exp(-s)-exp(-2*s))
;#-s^2-4*s-1+2*exp(-s)-exp(-2*s)

>

> oso1:=s^2+4*s+1;
oso2:=-2*exp(-s)+exp(-2*s);

> Y1:=oso1/nim;Y2:=oso2/nim;

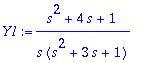
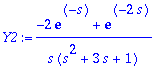
> Y1:=convert(Y1,parfrac,s);

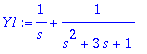
> Q2:=convert(1/nim,parfrac,s);

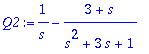
> y1:=IL(Y1,s,t);

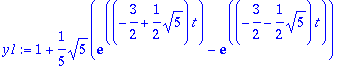
> y2:=IL(Y2,s,t);

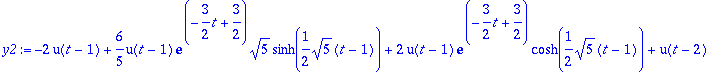
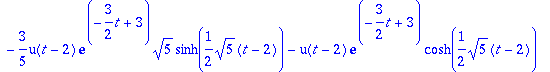
> convert(y2,exp);

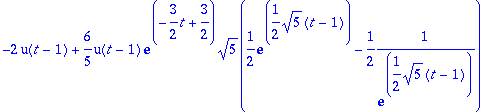
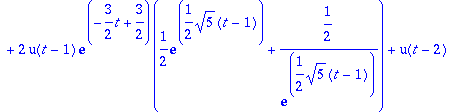
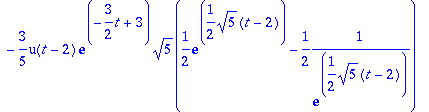
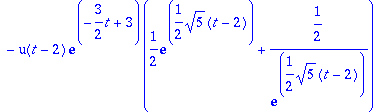
> convert(a,exp);

> yy:=y1+y2;

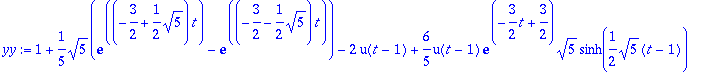
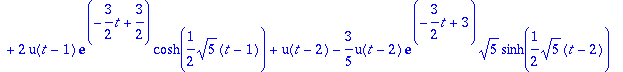
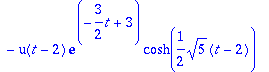
> plot([g,yy],t=0..4);

>