Harj. 3 LV
12.10.2001 HA
1.
> restart:
Warning, the name changecoords has been redefined
> yp:=t*(a*cos(w0*t)+b*sin(w0*t));
![]()
>
vasen:=simplify(diff(yp,t,t)+w0^2*yp);
oikea:=F0*cos(w0*t)/m;
![]()
![]()
> coeff(vasen,cos(w0*t))=coeff(oikea,cos(w0*t)),coeff(vasen,sin(w0*t))=coeff(oikea,sin(w0*t));
![]()
> solve({%},{a,b});
![]()
> assign(%);
> a,b;
![]()
> yp;
![]()
>
m:=1:F0:=1:w0:=10:plot(yp,t=0..30);
![[Maple Plot]](images/harj3lv8.gif)
2.
> restart:
Warning, the name changecoords has been redefined
> m:=2:k:=2: c:=1: r:=3*cos(3*t)-2*sin(3*t);
![]()
> yp:=a*cos(3*t)+b*sin(3*t);
![]()
> vasen:=m*diff(yp,t,t)+c*diff(yp,t)+k*yp;
![]()
> oikea:=r:
> coeff(vasen,cos(3*t))=coeff(oikea,cos(3*t)),coeff(vasen,sin(3*t))=coeff(oikea,sin(3*t));
![]()
> ab:=solve({%},{a,b});
![]()
> yp:=a*cos(3*t)+b*sin(3*t);
![]()
> r:=3*cos(3*t)-2*sin(3*t):
> Yp:=R*cos(kolmetee-delta);
![]()
> vasen:=subs(kolmetee=3*t,expand(Yp)); oikea:=yp;
![]()
![]()
> coeff(vasen,cos(3*t))=coeff(oikea,cos(3*t)),coeff(vasen,sin(3*t))=coeff(oikea,sin(3*t));
![]()
> solve({%},{R,delta});Rdelta:=allvalues(%);
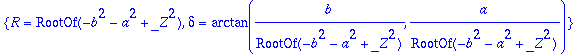
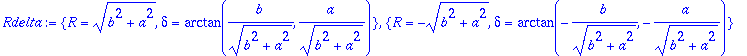
> assign(ab);
>
Tässä on syytä kirjoittaa kaavat käsin (mahd. leikkaus/liimaus), Maple ei ymmärrä merkeistä eikä oikeista haaroista.>
> R := sqrt(b^2+a^2); delta := arctan(b,a);
![]()
![]()
> R:=evalf(R); delta:=evalf(-arctan(41/42.)+Pi);
>
![]()
![]()
> y:='y': HY:=m*diff(y(t),t,t)+c*diff(y(t),t)+k*y(t)=0;
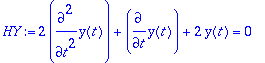
> m:=2:k:=2: c:=1:HY;
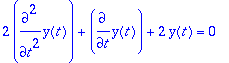
> dsolve(HY,y(t)): Yh:=rhs(%);
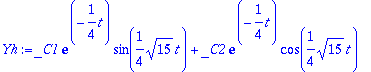
> Y:=unapply(Yh+yp,t);
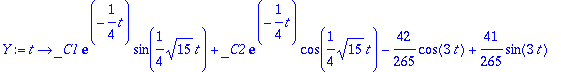
> solve({Y(0)=1,D(Y)(0)=0},{_C1,_C2});
![]()
> assign(%);
> Y(t);
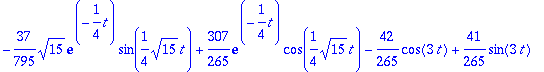
>
> Y(0);D(Y)(0);
![]()
![]()
> plot([r,Y(t),yp],t=0..15,color=[blue,red,green]);
![[Maple Plot]](images/harj3lv33.gif)
3.
> restart:
Warning, the name changecoords has been redefined
> r:=2*cos(omega*t);
![]()
> kar:=lambda^2+lambda/4+2=0;solve(%,lambda);
![]()
![]()
> yp:=a*cos(omega*t)+b*sin(omega*t);
![]()
> vasen:=diff(yp,t,t)+diff(yp,t)/4+2*yp;
![]()
> oikea:=r;
![]()
> coeff(vasen,cos(omega*t))=coeff(oikea,cos(omega*t)),coeff(vasen,sin(omega*t))=coeff(oikea,sin(omega*t));
![]()
> ab:=solve({%},{a,b});
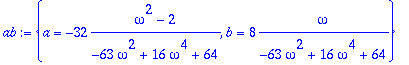
> Ampl:=sqrt(a^2+b^2);assign(ab);Ampl;simplify(%,symbolic);
>
![]()
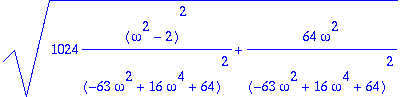
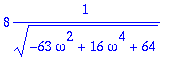
> g:=-63*omega^2+16*omega^4+64;dg:=diff(g,omega);solve(dg=0,omega);
![]()
![]()
![]()
> wmax:=%[2];evalf(%);
![]()
![]()
> plot(Ampl,omega=0..10);subs(omega=wmax,Ampl);
![[Maple Plot]](images/harj3lv50.gif)
![]()
> omega:=wmax:r;yp;
![]()
![]()
> plot([r,yp],t=0..20,color=[blue,red]);
![[Maple Plot]](images/harj3lv54.gif)
4.
> restart:
Warning, the name changecoords has been redefined
> yh:=A*cos(t)+B*sin(t); # Tämä jo osataan
![]()
> diff(yh,t,t)+yh; # Tarkistetaan kuitenkin.
![]()
> r:=3*cos(omega*t);yp:=a*cos(omega*t)+b*sin(omega*t);
![]()
![]()
> vasen:=diff(yp,t,t)+yp;oikea:=r:
> coeff(vasen,cos(omega*t))=coeff(oikea,cos(omega*t)),coeff(vasen,sin(omega*t))=coeff(oikea,sin(omega*t));ab:=solve({%},{a,b});
>
![]()
![]()
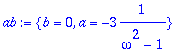
> assign(ab):
> yp;simplify(diff(yp,t,t)+yp); #Tarkistus.
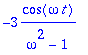
![]()
> Y:=unapply(yh+yp,t);
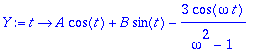
> A:='A':B:='B':AB:=solve({Y(0)=0,D(Y)(0)=2},{A,B});
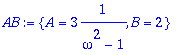
> assign(AB);
> Y(t);
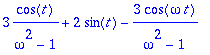
Amplitudi on hiukan huonosti asestettu tehtävä, yp:n amplitudi on näkyvissä suoraan, sensijaan koko Y:n amplitudi on hieman ongelmallinen, kun siinä lasketaan yhteen eri taajuksisia värähtelyjä.
>
plot([subs(omega=0.7,Y(t)),subs(omega=0.8,Y(t)),subs(omega=0.9,Y(t))],t=0..10,color=[red,green,blue]);
plot([subs(omega=0.7,Y(t)),subs(omega=0.8,Y(t)),subs(omega=0.9,Y(t))],t=0..50,color=[red,green,blue]);
![[Maple Plot]](images/harj3lv67.gif)
![[Maple Plot]](images/harj3lv68.gif)
> A:='A':B:='B': AB:=solve({Y(0)=1,D(Y)(0)=1},{A,B});assign(%);
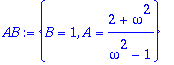
> Y(t);
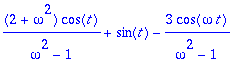
>
plot([subs(omega=0.7,Y(t)),subs(omega=0.8,Y(t)),subs(omega=0.9,Y(t))],t=0..10,color=[red,green,blue]);
plot([subs(omega=0.7,Y(t)),subs(omega=0.8,Y(t)),subs(omega=0.9,Y(t))],t=0..50,color=[red,green,blue]);
![[Maple Plot]](images/harj3lv71.gif)
![[Maple Plot]](images/harj3lv72.gif)
Huojunta näkyy selvänä lähimpänä 1:tä olevalla kulmataajuudella. Ratkaisut näyttävät laajemmalla aikaskaalalla aivan samoilta, alussa on eroa, kun katsotaan lyhemmällä skaalalla.
>
Jätetään nyt tähän.
Ehkä niitä oli todella hiukan liikaa!!
>
>