Harj. 2 LV

pe 28.9.01 HA

1.

> restart:

Warning, the name changecoords has been redefined

Picardin iteraatio:

> y[n](x):=y[0]+Int(f(t,y[n-1](t)),t=x[0]..x);

a)

> restart: f:=(x,y)->x+y; y[0]:=0:

Warning, the name changecoords has been redefined

> y[1]:=y[0]+simplify(int(subs(x=t,f(t,y[0])),t=0..x));

> y[2]:=y[0]+simplify(int(subs(x=t,f(t,y[1])),t=0..x));
y[3]:=y[0]+simplify(int(subs(x=t,f(t,y[2])),t=0..x));
y[4]:=y[0]+simplify(int(subs(x=t,f(t,y[3])),t=0..x));

> y[5]:=y[0]+simplify(int(subs(x=t,f(t,y[4])),t=0..x));
y[6]:=y[0]+simplify(int(subs(x=t,f(t,y[5])),t=0..x));
y[7]:=y[0]+simplify(int(subs(x=t,f(t,y[6])),t=0..x));
y[8]:=y[0]+simplify(int(subs(x=t,f(t,y[7])),t=0..x));
y[9]:=y[0]+simplify(int(subs(x=t,f(t,y[8])),t=0..x));

>
y[2]:=x^2/2+simplify(int(subs(x=t,y[1]),t=0..x));
y[3]:=x^2/2+simplify(int(subs(x=t,y[2]),t=0..x));
y[4]:=x^2/2+simplify(int(subs(x=t,y[3]),t=0..x));
y[5]:=x^2/2+simplify(int(subs(x=t,y[4]),t=0..x));
y[6]:=x^2/2+simplify(int(subs(x=t,y[5]),t=0..x));
y[7]:=x^2/2+simplify(int(subs(x=t,y[6]),t=0..x));

> ytarkka:=dsolve({diff(yy(x),x)=x+yy(x),yy(0)=0},yy(x));

>

> Y:=rhs(ytarkka);

> series(Y,x=0,10);

>

Aivan ilmeisesti tuottaa Taylorin sarjan, suppenee kaikkialla. (Kehitelmä voitaisiin todistaa induktiolla.)

b)

> restart: f:=(x,y)->x+y; y[0]:=-1:

Warning, the name changecoords has been redefined

>

> k:='k':for k to 10 do y[k]:=y[0]+simplify(int(subs(x=t,f(t,y[k-1])),t=0..x)); end do;
k;

>

> ytarkka:=dsolve({diff(yy(x),x)=x+yy(x),yy(0)=-1},yy(x));

> Y:=rhs(ytarkka);plot([Y,seq(y[k],k=0..10)],x=-3..3);

> plot([Y,y[10]],x=-5..5);

>

c)

> restart: f:=(x,y)->y^2; y[0]:=1:

Warning, the name changecoords has been redefined

> for k to 4 do y[k]:=y[0]+simplify(int(subs(x=t,f(t,y[k-1])),t=0..x)); end do;
k;

> y[2]:=series(y[2],x=0,4);y[3]:=series(y[3],x=0,8);y[4]:=series(y[4],x=0,16);

>

>

>

>

> ytarkka:=dsolve({diff(yy(x),x)=yy(x)^2,yy(0)=1},yy(x));
Y:=rhs(ytarkka);plot([Y,seq(y[k],k=0..4)],x=-1..1-0.1);
plot([Y,y[4]],x=-1..1-0.1);
plot(Y-y[4],x=-1..1-0.1);

> series(Y,x=0,7);

>

d)

> restart: f:=(x,y)->3*y/x; y[0]:=1:

for k to 3 do y[k]:=y[0]+simplify(int(subs(x=t,f(t,y[k-1])),t=1..x)); end do;

Warning, the name changecoords has been redefined

> y[4]:=y[0]+simplify(int(subs(x=t,f(t,y[3])),t=1..x));

> y[5]:=y[0]+simplify(int(subs(x=t,f(t,y[4])),t=1..x));

> ytarkka:=dsolve({diff(yy(x),x)=3*yy(x)/x,yy(1)=1},yy(x)); Y:=rhs(ytarkka);

> series(y[3],x=1,4);series(Y,x=1,4);

> series(y[4],x=1,4);series(Y,x=1,4);

> series(y[5],x=1,5);series(Y,x=1,4);

> plot([Y,seq(y[k],k=0..5)],x=0.2..2);plot([Y,y[4]],x=0.2..2);plot(Y-y[4],x=0.2..2);

2.

3.

4.

5.

6. Stabiilisuustarkasteluja

> restart:with(DEtools): with(plots):

Warning, the name changecoords has been redefined

> read("/home/apiola/opetus/peruskurssi/v2-3/301/maple/v301.mpl"); # Vaihda kommentit.

> # read("/p/edu/mat-1.414/maple/v301.mpl"); # Kurssihakemisto, näkyy luokissa.

> #op(Euler);op(RK4);op(BE);

> f:=(t,y)->-2*alpha*(t-1)*y;

> diff(f(t,y),y);

Tämä on < 0, kun t > 1 ja päinvastoin. Asian näkyy diffyhtälön ratkaisukäyräparvessa niin, että käyrät menevät "nippuun" (tai "suppuun"), kun

aika kasvaa lähdettäessä arvon t=1 oikealta puolelta ja vasemmalta taas päinvastoin.

> dyht:=diff(y(t),t)=-2*alpha*(t-1)*y(t):

> dsolve(diff(y(t),t)=-2*alpha*(t-1)*y(t),y(t));

> Y:=subs(_C1=C,rhs(%));

> alpha:=2:plot([seq(Y,C=[0.1,.5,0.6,0.7,-0.1,-0.2,-0.7])],t=-1..3);

No tässä tuo yllä mainittu niputuskäytös näkyy. Jos siis 1:n oikealta lähdetään epätarkalla alkuarvolla, niin yhtälön stabiilisuus on omiaan korjaamaan tilannetta. Toki asiat voivat silti mennä mäkeen, jos askelpituuden valinnassa ei oteta huomioon numeerisen menetelmän asettamaa stabiilisuusvaatimusta.

Piirretään ratkaisukäyrät vielä suuntakenttäpiirrokseen.

> display([DEplot(dyht,y(t),t=-1..3,y=-5..5,color=grey),plot([seq(Y,C=[0.1,.5,0.6,0.7,-0.1,-0.2,-0.7])],t=-1..3)]);

No niin, tehtäväpaperissa oleva kaava antaa EM:n stabiilisuusehdon:

> h < 2/abs(diff('f(t,y)',y));

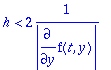
> dfy:=diff(f(t,y),y); # Muista: alpha:=2

> seq(evalf(dfy),t=[1,2,3,4,4.5]);

Jos käytämme vaikka kesimmäistä arvoa -8, saamme:

> h < 2/8; m=3.5/0.25;

> Euler(f,1,4.5,1,14);

> plot([%]);

> plot([Euler(f,1,4.5,1,7)]);h=3.5/7;

> EM6:=plot([Euler(f,1,4.5,1,6)]): h=3.5/6;

> suuntak:=DEplot(dyht,y(t),t=1..4.5,y=-5..5,color=grey):

> display(EM6,suuntak);

> BE6:=plot([BE(f,1,4.5,1,6,2)]): h=3.5/6;

> suuntak:=DEplot(dyht,y(t),t=1..4.5,y=-1..2,color=grey):

> display(BE6,suuntak);

> BE3:=plot([BE(f,1,4.5,1,3,2)]): h=3.5/3;

> display(BE3,suuntak);

Tämä on vakuuttavaa, vaikuttavaa, dramaattista! BE ottaa vain 3 askelta ja etenee horjumatta kohti oikeaa ratkaisua. Itse asiassa BE on aina stabiili, jos yhtälö on stabiili, siinä stabiilisuus ei aseta mitään rajoitusta askelpituudelle.