Harj. 1 av

syksy 2001 HA

1.

a)

> y:=C*exp(-x)+x^2-2*x; # RE

> vasen:=diff(y,x)+y;

> oikea:=x^2-2;

> vasen=oikea;

Tarkistus oli helppoa. Miten sitten löytäisimme RE:n Katotaan, osaako Maple.

Maplessa on dsolve-komento diffyhtälöihin. Kokeillaan, osaako se..

> y:='y':x:='x':

> dy:=diff(y(x),x)+y(x)=x^2-2; # Diffyhtälön esitysmuoto

> dsolve(dy,y(x));

>

b)

> y:=a*cos(x)+b*sin(x);

> diff(y,x,x)+y;

Kyllä vaan! Kokeillaan taas dsolvea:

> y:='y':

> dsolve(diff(y(x),x,x)+y(x)=0,y(x));

Kyllä kyllä!

c)

> d3y:=exp(x);

> d2y:=int(dy3,x)+c1;

> d1y:=int(dy2,x)+c2;

> y:=int(dy1,x)+c3;

>

Tarkistus:

> diff(y,x,x,x);

> y:='y': dsolve(diff(y(x),x,x,x)=exp(x),y(x));

>

d)

> restart:

Warning, the name changecoords has been redefined

> RE:=x^2+y(x)^2=C;

> diff(RE,x);

> dsolve(%,y(x),implicit);

> dsolve(%%,y(x));

>

2.

> restart:

Warning, the name changecoords has been redefined

> y:=t->y0*exp(k*t);

> y0:=5.3:

> solve(y(1)=13,k);

> k:=%:

> y(1);

> Y:=[5.3,13,31,63,106,150,230];

> seq([1800+30*(j-1),Y[j],evalf(y(j-1))],j=1..7);

> Matrix([%]);

>

3.

Kts. [HAM] s. 169-170

> restart:with(DEtools): with(plots):

Warning, the name changecoords has been redefined

> dyht:=diff(y(x),x)=y(x)-x;

> DEplot(dyht,y(x),x=-2..2,y=-2..2);

> DEplot(dyht,y(x),x=-2..2,y=-2..2,[[y(0)=-1],[y(0)=0],[y(0)=1],[y(0)=2]]);

Huomaamme, että suuntakenttien ja ratkaisukäyrien (toki myös isokliinien) piirtäminen

käy mukavasti myös Maplella. Hiiri-inputtia ei saada mukaan, homma on vaikeammissa

tapauksissa epätarkempaa ja hitaampaa. (Numeerinen menetelmä ei ole "adaptiivinen".)

Mutta, ei tämäkään hassumpaa, vai mitä!

4.

> dyht:=diff(y(x),x)=-4*x/y(x);

> skuva:=DEplot(dyht,y(x),x=-1..1,y=-1..1,color=grey):

> rkuva:=implicitplot({seq(4*x^2+y^2=C,C=[0.1,0.2,0.5,1])},x=-2..2,y=-2..2,grid=[40,40]):

> display([skuva,rkuva]);

>

6.

Tämä tehtävä oli sinänsä mielestäni onnistunut ja Mari sen mukavasti esitteli.

> dy8:=diff(x(t),t)=t*x(t)^2+t^2;

> infolevel[dsolve]:=3:ratk:=dsolve(dy8,x(t));infolevel[dsolve]:=0:

Methods for first order ODEs:

Trying to isolate the derivative dx/dt...

Successful isolation of dx/dt

-> Trying classification methods

trying a quadrature

trying 1st order linear

trying Bernoulli

trying separable

trying inverse linear

trying homogeneous types:

trying Chini

differential order: 1; looking for linear symmetries

trying exact

Looking for potential symmetries

-> Trying 2nd set of classification methods

trying Riccati

trying Riccati sub-methods

trying Riccati to 2nd Order

   *** Sublevel 2 ***

   Methods for second order ODEs:

   Trying to isolate the derivative d^2Y/dX^2...

   Successful isolation of d^2Y/dX^2

   -> Trying classification methods

   trying a quadrature

   trying a symmetry of the form [xi=0, eta=F(x)]

      testing BRANCH 1 ->

      testing BRANCH 2 ->

      testing BRANCH 3 ->

      testing BRANCH 4 ->

   checking Euler equation

   checking for special function equations

   Special function equations successful

Riccati to 2nd Order successful

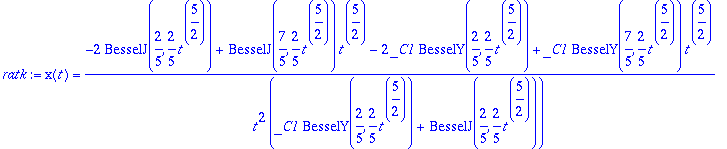
> X:=subs(ratk,x(t)):

> plot(subs(_C1=1,X),t=-2..2);

>