Harj. 12 LV

Tämä on nyt ehdottomasti viimeinen s. 2001

1.

> restart: with(inttrans): alias(u=Heaviside):

Warning, the name changecoords has been redefined

> f:=x->alpha*exp(-alpha*x);

> assume(alpha>0):int(f(x),x=0..infinity);

> plot(subs(alpha=2,u(x)*f(x)),x=-1..4,axes=box);

> mu:=int(x*f(x),x=0..infinity);

> sigma^2=int((x-mu)^2*f(x),x=0..infinity);

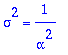
Huom! Yllä olevat integraalit voidaan nähdä myös Laplace-muunnoksina:

> restart: with(inttrans): mu=alpha*laplace(t,t,alpha);

Warning, the name changecoords has been redefined

> sigma^2=alpha*laplace((t-mu)^2,t,alpha);subs(mu = 1/alpha,%);

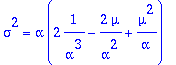
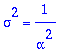
2.

> restart: with(inttrans): alias(u=Heaviside):with(plots):with(plottools):

Warning, the name changecoords has been redefined

> f:=x->alpha*exp(-alpha*x);

> F:=unapply(int(f(t),t=0..x),x);

> alpha:=1/2000:

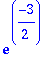
> 1-F(3000);evalf(%);

> display(plot(f(t),t=0..3000),plot(f,3000..8000,filled=true,color=yellow));

> x0:=3000:

> display(plot(F,0..8000),line([0,F(x0)],[x0,F(x0)]),line([x0,0],[x0,F(x0)]));

>

3.

> restart; with(plots):

Warning, the name changecoords has been redefined

> F:=x->Phi((x-mu)/sigma);

> Phi:=x->1/2+1/2*erf(x/sqrt(2));

> mu:=10: sigma:=0.02:

a)

> F(9.97);evalf(%);

b)

> 1-F(10.05): evalf(%);

c)

> (1-F(10.03))+F(9.97): evalf(%);

>

>

4.

(d)

> g:=1-(F(mu+c)-F(mu-c))-0.05;

> plot(g,c=sigma..3*sigma);

> cc:=fsolve(g=0,c=0.04);

> vali:=mu-cc,mu+cc;

e) Muutetaan odotusarvoa: Kaksi mahdollista tapaa ajatella: 1) Tarkastellaan koko ajan väliä

> ['mu' -c, 'mu'+c];

2) Pidetään kohdassa d) saatu väli [9.960800720, 10.03919928] kiinteänä ja muutetaan keskiarvoa mu (hiukan). Tämä liittyy paremmin "elävään elämään".

Tapauksess 1) kysymystä voidaan enemmän pitää "kompakysymyksenä": Tapauksessa 2) on kylläkin epärealistista muuttaa keskiarvoa noin paljon.

Järkevämpi muutos olisi mu=10.01. (Tällä arvolla laskin taululla.)

> mu:=10.1:g:=1-(F(mu+c)-F(mu-c))-0.05;

> fsolve(g=0,c=0.04);

Muutetaan oikein kunnolla.

> mu:=100:g:=1-(F(mu+c)-F(mu-c))-0.05;fsolve(g=0,c=0.04);

Tulos on riippumaton :stä tietenkin:

> restart: F:=x->Phi((x-mu)/sigma);

Warning, the name changecoords has been redefined

> F(mu-c),F(mu+c);

> P("hylätään")=1-(F(mu+c)-F(mu-c));

Tulos ei tosiaankaan riipu :stä.

Sievenee vielä hiukan:

> P("hylätään")=1-2*Phi(c/sigma);

Muistetaan: (Ylimääräinen harjoitustehtävä)

> Phi(-x)=1-Phi(x);

Tapaus e 2)

> vali;

> mu:=10.01;

> P("hylätään")=1-(F(vali[2])-F(vali[1]));evalf(%);

Siis hylkäysprosentiksi tuli n. 8 % (d)-kohdan 5%:n sijasta.