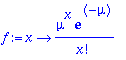
Harj. 12 AV

5.12.2001 HA

1.

> restart:

Warning, the name changecoords has been redefined

> f:=x->mu^x/x!*exp(-mu);

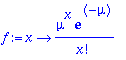
> 1-sum(f(x),x=0..1);subs(mu=1/2,%);evalf(%);

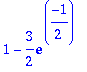
2.

> restart:

Warning, the name changecoords has been redefined

> f:=x->mu^x/x!*exp(-mu);

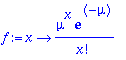
> P_alle_5:=sum(f(x),x=0..4);subs(mu=5,%);evalf(%);

Nämä olisivat sopineet olemaan a)- ja b)-kohta samasta tehtävästä, mutta olkoon kompensaationa menneistä työläisyyksistä.

3.

Pohdiskellaan hieman Poissonin jakaumaa tässä yhteydessä KRE exe 3:n s. 1082 hengessä.

Siinä otetaan esimerkisi parkkipaikka, johon tulee keskimäärin 2 autoa minuutissa. Kysytään, millä todennäköisyydellä satunnaisesti valitun minuutin aikana saapuu x autoa

(tai jokin vastaava kysmys, johon jakaumafunktion avulla voidaan vastata).

Yleisemmin voidaan ottaa 2:n auton sijaan

autoa.

Jaetaan 1 min aikaväli pieniin osiin, n kpl. Todennäköisyys, että näistä keskimäärin :sta sisään tulevasta autosta jokin osuu tietylle osavälille :

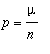
Tilannetta voidaan ajatella toistokokeena, jossa näitä pieniä aikavälejä vedetään aikasäkistä.

Näin saadaan

> f:=x->B(n,x)*p^x*(1-p)^(n-x); # B on binomikerroin

Kun n kasvaa, niin jakauma lähenee Poissonia ( ).

Sitten varsinaiseen tehtävään: Otetaan tämä exa 3 lähtökohdaksi.

> restart: with(combinat): alias(B=binomial):

Warning, the name changecoords has been redefined

Warning, the protected name Chi has been redefined and unprotected

> fB:=x->B(n,x)*p^x*(1-p)^(n-x);
fP:=x->mu^x/x!*exp(-mu);

>

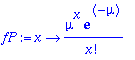
> mu:=2: p:=mu/n;

> n:=10:plot([fB(x),fP(x)],x=0..n,color=[blue,pink]);

> sum(fB(x),x=0..5);evalf(%);sum(fP(x),x=0..5);evalf(%);

> n:=20:plot([fB(x),fP(x)],x=0..n,color=[blue,red]);sum(fB(x),x=0..5);evalf(%);sum(fP(x),x=0..5);evalf(%);

> n:=30:plot([fB(x),fP(x)],x=0..n,color=[blue,black]);

> n:=60:plot(fB(x)-fP(x),x=0..10);

4.

> restart:

Warning, the name changecoords has been redefined

> with(inttrans):alias(u=Heaviside): # alias(u=inttrans[Heaviside]):

a)

> Int(a+b*t,t=30..90): %=value(%);

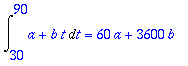
> rhs(%)=1,a+90*b=0;

> solve({%},{a,b});

> f:=unapply((u(t-30)-u(t-90))*subs(%,a+b*t),t);

> plot(f,20..100);

> Int(f(t),t=-infinity..infinity): %=value(%); # Tarkistus.

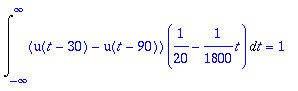
> F:=int(f(x),x=-infinity..t);F:=collect(%,{u(t-30),u(t-90)});

> plot(F,t=20..100,axes=box);

> convert(F,piecewise);

b)

> FF:=unapply(F,t);

> FF(60)-FF(40);evalf(%);

> 1-FF(60);

c)

> mu:=int(t*f(t),t=30..90);

> int((t-mu)^2*f(t),t=30..90);sqrt(%);evalf(%);

5.

> restart: with(combinat): alias(B=binomial):

Warning, the name changecoords has been redefined

Warning, the protected name Chi has been redefined and unprotected

> f:=x->B(M,x)*B(N-M,n-x)/B(N,n);

> N:=20: M:=5: n:=3:

> f(x);f(0),f(1),f(2),f(3);evalf(%);

> plot(f,0..3);plot([seq([x,f(x)],x=[$0..3])],style=point,symbol=cross,symbolsize=20,axes=box);

> with(plots):with(plottools):display([seq(line([x,0],[x,f(x)]),x=[$0..3])],color=blue,axes=box,linestyle=6,thickness=2);

>

6.

> restart:

Warning, the name changecoords has been redefined

> with(plots):

> F:=x->Phi((x-mu)/sigma);

> toda:=1-F(x1);

> mu:=12000: sigma:=2000: x1:=15000: toda;

> Phi:=x->1/2+1/2*erf(x/sqrt(2));

> toda;evalf(%);

> f:=x->1/(sigma*sqrt(2*Pi))*exp(-1/2*((x-mu)/sigma)^2);

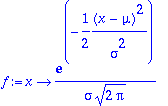
> display(plot(f,mu-3*sigma..x1),plot(f,x1..mu+3*sigma,filled=true,color=red));

b)

> 1-F(x)=0.02;

> plot(lhs(%)-rhs(%),x=mu+sigma..mu+3*sigma);

> x2:=fsolve(1-F(x)=0.02,x=16000);plot(f,x1..x2);

>

>