V3 Välikoe 3 kevät 2002
6.5.02 HA
Huomioita
Tue May 7 12:03:56 EEST 2002Pikainen silmäily koepapereihin näyttää sen suuntaiselta, että tehtävät 2 ja 3 ovat tuottaneet monelle vaikeuksia. Tehtävät on valittu niin, että laskuteknisesti ne eivät ole työläitä (ja integrointiapukin on annettu).
Sinänsä tuollaisen tehtävän hahmottaminen niin, että integrointirajat saadaan määrätyksi, on kai sellainen asia, että se kaipaisi hieman lisäharjoitusta. Kannattaa nyt lukea tämä teksti ja käsinkirjoitettu. Viimeksi mainittuja on saatavana ovenpielestäni.
Annan mahdollisuuden korottaa arvosanaa tekemällä tähän liittyviä lisätehtäviä sopimuksen mukaan.
Kokeiden palauttamisaikataulua en osaa vielä sanoa.
> #xd:=[-1,0,1]: yd:=[0,2,1]:
> psi:=x->a+b*x; # Malli (tässä 1. asteen polynomi)
![]()
> f:=(a,b)->sum((yd[i]-psi(xd[i]))^2,i=1..3);
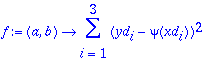
> xd:=[-1,0,1]: yd:=[0,2,1]:
> f(a,b);
![]()
> dfa:=diff(f(a,b),a);
![]()
> dfb:=diff(f(a,b),b);
![]()
> solve({dfa=0,dfb=0},{a,b});
![]()
> assign(%);
> psi(x);
![]()
Tässä kaikki . (Kuva on alla.)
Tehtävän data on valittu laskutyön kannalta mahdollisimman ystävällisesti.
Yhtälösysteemi on "kytkemätön", eli matriisina on diagonaalimatriisi.
Tarkistukseksi ja mielen virkistykseksi
lasketaan nyt vielä yleisesti johdetulla kaavalla:
> C:=<<1,1,1>|<op(xd)>>;
![C := _rtable[137546432]](images/vk38.gif)
> CT:=Transpose(C);
![CT := _rtable[137618232]](images/vk39.gif)
> M:=CT.C;
![M := _rtable[136983808]](images/vk310.gif)
> B:=CT.Vector(yd);
![B := _rtable[138321632]](images/vk311.gif)
> ab:=LinearSolve(M,B);
![ab := _rtable[136849908]](images/vk312.gif)
> suora:=1+x/2;
![]()
> data:=plot([seq([xd[i],yd[i]],i=1..3)],view=[-2..2,-1..3],style=point,symbol=circle,symbolsize=17,axes=box):
> display(data,plot(suora,x=-2..2,color=blue));
![[Maple Plot]](images/vk314.gif)
>
2.
> restart:
Warning, the name changecoords has been redefined
> with(plots):
> with(plottools):
> setoptions3d(axes=boxed,orientation=[-30,50],scaling=constrained):
> ymp:=plot([cos(t),sin(t),t=-Pi/4..Pi/3],x=-1..1,y=-1..1,scaling=constrained):
> display(ymp,line([0,0],[1/2,sqrt(3)/2]),line([0,0],[1/sqrt(2),-1/sqrt(2)]));
![[Maple Plot]](images/vk315.gif)
> parabo:=plot3d([r*cos(Theta),r*sin(Theta),1-r^2],Theta=-Pi/4..Pi/3,r=0..1):
>
seinaplus:=plot3d([r*cos(Pi/3),r*sin(Pi/3),z],z=0..1-r^2,r=0..1,style=wireframe):
seinamiinus:=plot3d([r*cos(-Pi/4),r*sin(-Pi/4),z],z=0..1-r^2,r=0..1,style=wireframe):
> display(parabo,seinaplus,seinamiinus,labels=["x","y","z"]);
![[Maple Plot]](images/vk316.gif)
>
Lasku lieriökoordinaateissa
> massa:=Int(rho(x,y,z),v);
![]()
> Massa:=Int(Int(r*Int(a*r*cos(Theta)*z,z=0..1-r^2),r=0..1),Theta=-Pi/4..Pi/3);
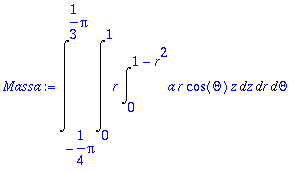
> massa:=factor(value(Massa));
![]()
Lasku xyz-koordinaatistossa
> m1:=Int(Int(Int(a*x*z,z=0..1-x^2-y^2),x=-y..sqrt(1-y^2)),y=-1/sqrt(2)..0);
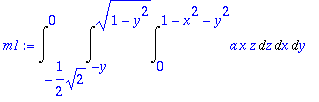
> m1:=value(%);
![]()
> m2:=Int(Int(Int(a*x*z,z=0..1-x^2-y^2),x=y/sqrt(3)..sqrt(1-y^2)),y=0..sqrt(3)/2);
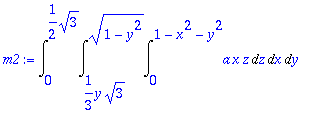
> m2:=value(m2);
![]()
> factor(m1+m2);
![]()
> Int(Int(int(a*x*z,z=0..1-x^2-y^2),x=-y..sqrt(1-y^2)),y=-1/sqrt(2)..0);
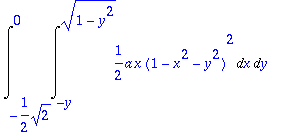
> m1:=Int(int(int(a*x*z,z=0..1-x^2-y^2),x=-y..sqrt(1-y^2)),y=-1/sqrt(2)..0);
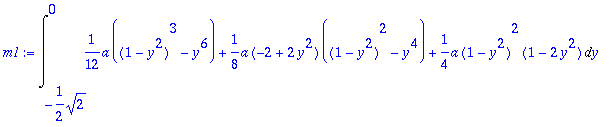
> simplify(1/12*a*((1-y^2)^3-y^6)+1/8*a*(-2+2*y^2)*((1-y^2)^2-y^4)+1/4*a*(1-y^2)^2*(1-2*y^2));
![]()
Käsin laskussa simplify olisi se eniten kaivattu apu. Integroinnissa pärjätään pelkällä polynomien integroinnilla, mutta sieventäminen on vaivalloista.
3.
Piirrellään aluksi.
> x:='x': y:='y': z:='z': a:='a':
> x:=u*cos(v); y:=u*sin(v);z:=u;
![]()
![]()
![]()
> X:=a*cos(Theta): Y:=a+a*sin(Theta):
> a:=2:
> kartio:=plot3d([x,y,z],u=0..2*a,v=0..2*Pi):
>
lierio:=plot3d([X,Y,Z],Theta=0..2*Pi,Z=0..2*a,color=red,style=wireframe):
> display(kartio,lierio);
![[Maple Plot]](images/vk331.gif)
> kartionosa:=plot3d([x,y,z],v=0..Pi,u=0..2*a*sin(v)):
> display(kartionosa,lierio);
![[Maple Plot]](images/vk332.gif)
> taso:=plot3d([xx,yy,yy],xx=-2..2,yy=0..4):
> display(lierio,taso);
![[Maple Plot]](images/vk333.gif)
Voit valoisina kesäiltoina miettiä, miksi lieriön ja tason leikkauksen pinta-ala on sama kuin kysytty kartion vaippapinta (kun puhutaan nyt siitä yläosasta).
Laskutapa 1
> restart:with(LinearAlgebra):
Warning, the name changecoords has been redefined
> with(linalg):
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
Kartion parametriesitys:
> x:=u*cos(v): y:=u*sin(v): z:=u:
v on lieriökoordinaatiston
![]() ja u on r .
ja u on r .
> R:=[x,y,z];
![]()
> Ru:=map(diff,R,u);
![]()
> Rv:=map(diff,R,v);
![]()
> crossprod(Ru,Rv);map(factor,%);RuxRv:=map(simplify,%);
![]()
![]()
![]()
Tämän ristitulon normi on pinta-alkioiden muuntosuhde.
> sum(RuxRv[i]^2,i=1..3);
![]()
> simplify(%);
![]()
> normi:=simplify(sqrt(%),symbolic);
![]()
Ilman "symbolic"-lisäystä Maple ei uskalla tehdä sievennystä
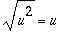 ( mikä ei yleisesti ole tosi, käyttäjälle vastuu!)
( mikä ei yleisesti ole tosi, käyttäjälle vastuu!)
> a:=2:plot([a*cos(Theta),a+a*sin(Theta),Theta=0..2*Pi],scaling=constrained);
![[Maple Plot]](images/vk345.gif)
> display(plot3d([r*cos(Theta),r*sin(Theta),0],Theta=0..Pi,r=0..2*a*sin(Theta),labels=["x","y","z"]),plot3d([r*cos(Theta),r*sin(Theta),1],Theta=0..Pi,r=0..2*a*sin(Theta)));
![[Maple Plot]](images/vk346.gif)
Tässä vain tarkistimme, että integrointirajat napakoordinaateissa ovat oikein (piirrettiin kaksi ympyrälevyä päällekkäin).
> a:='a':
> Ala:=2*Int(Int(normi,u=0..2*a*sin(v)),v=0..Pi);
>
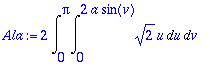
> ala:=value(Ala);
![]()
> 2*Int(int(normi,u=0..2*a*sin(v)),v=0..Pi); # Välivaihe.
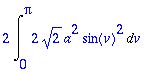
>
Laskutapa 2
> restart:
Warning, the name changecoords has been redefined
> f:=sqrt(x^2+y^2); # Kartiopinta void, esittää näin.
![]()
> suhde2:=diff(f,x)^2+diff(f,y)^2+1;
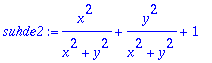
> simplify(%);
![]()
> suhde:=sqrt(%);
![]()
> ala:=2*Int(Int(suhde,x),y);
![]()
Integroimisalueena on a-säteinen kiekko, joten tulos on kerroin*a-säteisen ympyrän ala.
> ala:=2*sqrt(2)*Pi*a^2;
![]()
>
4.
> restart:
Warning, the name changecoords has been redefined
a)
Sama kuin harj 12 av teht. 4
Määrättävä solmut x1,x2 ja painot w1,w2 siten, että integrointikaava
> Int(f(x),x=-1..1)=w[1]*f(x[1])+w[2]*f(x[2]);
![Int(f(x),x = -1 .. 1) = w[1]*f(x[1])+w[2]*f(x[2])](images/vk356.gif)
on tarkka kaikille astetta 3 oleville polynomeille. Välttämätöntä ja riittävää: tarkka kaikille monomeille
> 1,x,x^2,x^3;
![]()
> Gauss2yht:={seq(Int(x^k,x=-1..1)=w1*x1^k+w2*x2^k,k=0..3)};
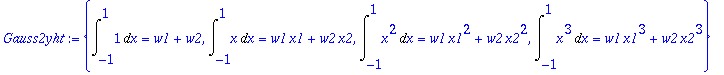
Muutetaan Int -> int, jolloin integraalit lasketaan:
> gauss2yht:={seq(int(x^k,x=-1..1)=w1*x1^k+w2*x2^k,k=0..3)};
![]()
> solve(gauss2yht,{x1,x2,w1,w2});map(allvalues,%);
![]()
![]()
> x1 := -1/3*sqrt(3); x2 := 1/3*sqrt(3); w1 := 1; w2 = 1;
![]()
![]()
![]()
![]()
> restart:
Warning, the name changecoords has been redefined
Käsin laskien nähdään heti, että valitsemalla w1=w2=1 ja x1 = -x2, saadaan 2 ensimmäistä yhtälöä toteutumaan. Kolmas tulee silloin muotoon:
> 2/3 = subs(w1=1,w2=1,x1=-x2,w1*x1^2+w2*x2^2);
![]()
Tästä saadaan:
> solve(%,x2);
![]()
x2:lla merkitsimme positiivista, joten
> x2:=max(%);
![]()
Sitten on vain todettava, että saadut ratkaisut toteuttavat myös neljännen:
> 0 = subs(w1=1,w2=1,x1=-x2,w1*x1^3+w2*x2^3);
![]()
Näin tapahtuu, joten olemme saaneet tehtävälle ratkaisun.
b)
> restart:
Warning, the name changecoords has been redefined
> Int(Int(f(x,y),y=-1..1),x=-1..1);
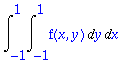
> F:=x->Int(f(x,y),y = -1 .. 1);
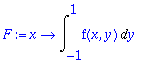
Sovelletaan tähän yhden muuttujan funktioon Gaussin kaavaa:
> G:=w1*F(x1)+w2*F(x2);
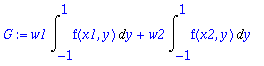
Sovelletaan kumpaankin integraaliin Gaussia:
>
G1:=w1*f(x1,y1)+w2*f(x1,y2);
G2:=w1*f(x2,y1)+w2*f(x2,y2);
![]()
![]()
> G:=w1*G1+w2*G2;
![]()
> w1:=1: w2:=1: x1:=-1/sqrt(3): x2:=-x1: y1:=x1: y2:=x2:
> G;
![]()
>
Kyseessä on siis Riemannin summa, jossa neliö jaetaan neljään alaltaan 1 olevaan pikkuneliöön ja kussakin tällaisessa lasketaan f:n arvo ao. Gauss-pisteparissa.