H/ratk/harj 7.mws (AV ja LV )
2002 HA
Katso mallia myös luentotyöarkilta L/mtaylor.mws
> restart:
> with(linalg): with(LinearAlgebra): with(plots):
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
Warning, the name changecoords has been redefined
> setoptions3d(axes=boxed,orientation=[-30,50],style=patchcontour):
> alias(Tr=Transpose):
>
1 AV ja 2LV
> f:=(x,y)->cos(x+sin(y));
![]()
1. derivaatat:
Katsotaan ensin derivaattafunktioita, vaikka niitä ei Maplella laskettaessa tarvitsisi edes nähdä:
> D[1](f),D[2](f),D[1,1](f), D[1,1,2](f),D[1,2,2,2](f);
![]()
![]()
![]()
Lasketaan sitten systemaattisesti kehityspisteessä p=(0,0).
> p:=0,0;
![]()
> D1f:=D[1](f)(p);D2f:=D[2](f)(p);
![]()
![]()
> D11f:=D[1,1](f)(p);D12f:=D[1,2](f)(p);D22f:=D[2,2](f)(p);
![]()
![]()
![]()
> D111f:=D[1,1,1](f)(p);D112f:=D[1,1,2](f)(p);D122f:=D[1,2,2](f)(p);D222f:=D[2,2,2](f)(p);
![]()
![]()
![]()
![]()
> T2:=f(p)+(D1f*h1+D2f*h2)+(1/2)*(D11f*h1^2+2*D12f*h1*h2+D22f*h2^2);
![]()
> h1:=0.1: h2:=-0.2:
> T2;
![]()
> f(h1,h2);
![]()
> f(h1,h2)-T2;
![]()
Tämä on samalla suhteellinen virhe. Tässä tapauksessa, kun kolmannet derivaatat O:ssa ovat nollia, kyseessä on samalla 3. asteen Taylorin polynomi ja jäännöstermi on siten jopa || h^4|| O(h).
LV
"Tuotantoajossa" emme turhan takia ota väliapumuuttujia, vaan kirjoitamme suoraan:
> h1:='h1': h2:='h2':
> Tay[4]:=T2+(1/4!)*(D[1,1,1,1](f)(p)*h1^4+4*D[1,1,1,2](f)(p)*h1^3*h2+6*D[1,1,2,2](f)(p)*h1^2*h2^2+4*D[1,2,2,2](f)(p)*h1*h2^3+D[2,2,2,2](f)(p)*h2^4);
![]()
> mtaylor(f(x,y),[x=0,y=0],5);
![]()
Oikein meni, mutta alkaa olla tuskaista ja virhealtista.
Eleganteimmasta päästä oleva oma koodi olisi se, jonka kirjoitin työarkille mtaylor.mws
Tässä on sekin hienous, että käyttäjän tarvitsee tuntea vain 1. muuttujan Taylorin lause, Maple johtaa sen ja ketjusäännön avulla laskiessaan samalla kahden muuttujan kaavan.
Hintana tälle mukavuudella on
a) laskenta on aika hidasta ja b) tuossa jouduin hieman kokeilemaan oikeanlaista järjestystä komenoille.
1) Osaamme periaatteessa laskea käsin editoiden (tarpeen mukaan Maplea esim. binomikaavan laskijana hyödyntäen).
2) Opetteluvaiheen jälkeen tositarpeeseen voimme aina käyttää mtaylor -funktiota.
Katsotaan piirtämistä seuraavassa tehtävässä. Tässä voitaisiin tehdä aivan samoin, mutta antaapa olla.
2 AV ja 1 LV
> f:=(x,y)->1/(2+x-2*y);p:=(2,1);
![]()
![]()
1. derivaatat:
Katsotaan ensin derivaattafunktioita, vaikka niitä ei Maplella laskettaessa tarvitsisi edes nähdä:
> D[1](f),D[2](f);
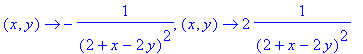
Lasketaan näiden arvot kehityspisteessä p:=(2,1):
> D1f:=D[1](f)(p);D2f:=D[2](f)(p);
![]()
![]()
2. derivaatat:
> D[1,1](f);
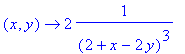
Pysyvät käsinlaskukelpoisina, kun sisäfunktioista tulee vain vakioita. Lasketaan taas kehityspisteessä:
> D11f:=D[1,1](f)(p);D12f:=D[1,2](f)(p);D22f:=D[2,2](f)(p);
![]()
![]()
![]()
3. derivaatat:
> D111f:=D[1,1,1](f)(p);D112f:=D[1,1,2](f)(p);D122f:=D[1,2,2](f)(p);D222f:=D[2,2,2](f)(p);
![]()
![]()
![]()
![]()
>
T3:=f(p)+(D1f*h1+D2f*h2)+
(1/2)*(D11f*h1^2+2*D12f*h1*h2+D22f*h2^2)+
(1/3!)*(D111f*h1^3+4*D112f*h1^2*h2+4*D122f*h1*h2^2+D222f*h2^3);
![]()
> T3:=subs(h1=x-2,h2=y-1,T3);
![]()
![]()
> H:=0.6:display([plot3d(f(x,y),x=2-H..2+H,y=1-H..1+H),plot3d(T3,x=2-H..2+H,y=1-H..1+H,color=yellow)]);
![[Maple Plot]](images/harj737.gif)
> display([plot3d(T3,x=2-H..2+H,y=1-H..1+H,color=yellow)]);
![[Maple Plot]](images/harj738.gif)
3 AV
> restart:
Neliömuoto pääakselikoordinaattien avulla lausuttuna on
> q:=Sum(lambda[i]*y[i]^2,i=1..n);
![q := Sum(lambda[i]*y[i]^2,i = 1 .. n)](images/harj739.gif)
4 AV
> alias(IdM=IdentityMatrix,IM=MatrixInverse):
> A:=<<a,c>|<c,b>>;
![A := _rtable[7300004]](images/harj743.gif)
> p:=det(A-lambda*IdM(2)); # Tässä on käytettävä linalgin det-funktiota, LinearAlgebran Determinant menee kummallisen virheeseen.
![p := det(-lambda*IdM(2)+_rtable[7300004])](images/harj744.gif)
> p:=collect(p,lambda); #p:=algsubs(a*b-c^2=detA,%);
![p := det(-lambda*IdM(2)+_rtable[7300004])](images/harj745.gif)
> expand((lambda-lambda[1])*(lambda-lambda[2])): collect(%,lambda);
![]()
(Karakteristisen polynomin korkeimman asteen termin kerroin on (-1)^n, tässä n=2.)
5 AV , 3LV
> f:=x^3+y^3-3*x*y;g:=grad(f,[x,y]);
![]()
![]()
Lasketaan ensin "käsin":
x^2 =y
y^2=x
=> x^4 = x => x=0 tai x=1
Saadaan pisteet (0,0) ja (1,1). Nämä ovat KRP:t.
Katsotaan, miten Maplen solve pärjää:
> ratkaisujoukot:=solve({g[1]=0,g[2]=0},{x,y});#allvalues(%[3]);
![]()
Saatiin samat reaaliset ratkaisut ja lisäksi muotoa RootOf olevia polynomiyhtälöitä:
> ratkaisujoukot[3];
![]()
> allvalues(%);
![]()
Komento allvalues yrittää ratkaista RootOf-muotoja ja onnistuu saamaan kompleksiratkaisuja. Niistä emme ole kiinnostuneita. Onneksi osasimme päätellä, että tuossa yllä olivat kaikki reaaliset ratkaisut, tiedämme siten, että tässä tapauksessa Maple löysi ne kaikki. (No, tehtävä ei ollut vaikea!)
> KRP:=<0,0>,<1,1>;
![KRP := _rtable[7406764], _rtable[7406804]](images/harj752.gif)
> H:=Matrix(hessian(f,[x,y]));H00:=subs(x=0,y=0,H);H11:=subs(x=1,y=1,H);
Error, (in Matrix) dimension parameters are required for this form of initializer
![]()
![]()
Käsin laskiessa päästään vähällä laskemalla det:
> det(H00);
![]()
Maplella voidaan yhtä hyvin laskea suoraan ominaisarvot.
> Eigenvalues(H00);
![]()
Johtopäätös on sama: ominaisarvot erimerkkiset, joten (0,0) on satulapiste.
> det(H11),trace(H11);
![]()
Trace laskee diagonaalialkioiden summan (tietysti riittää katsahtaa matriisiin päin nähdäkseen, että molemmat diagonaalialkiot ovat positiivisia).
Katsotaan nyt vielä suoraan:
> Eigenvalues(H11);
![]()
Varmaakin varmemmin: ominaisarvot positiiviset => (1,1) on min-piste.
> H:=0.5:plot3d(f,x=-H..H,y=-H..H,style=patchcontour,title="Satulapiste (0,0)");plot3d(f,x=1-H..1+H,y=1-H..1+H,style=patchcontour,title="Minimipiste (1,1)");
>
![[Maple Plot]](images/harj759.gif)
![[Maple Plot]](images/harj760.gif)
Siistiä!
> plot3d(f,x=-2..3,y=-2..3,style=patchcontour,title="Laajempi alue");
![[Maple Plot]](images/harj761.gif)
>
4 LV
> f:=cos(x)+cos(y):
> nablaf:=grad(f,[x,y]);
![]()
KRP: sin(x)=0
sin(y)=0
Ratk:
![]() ,
,
![]() .
.
Lasketaan Hessen matriisi kriittisissä pisteissä. Tehdään laskut "käsin"
> H:=Matrix([[f11,f12],[f12,f22]]);
![H := _rtable[7759808]](images/harj765.gif)
> f11:=diff(nablaf[1],x);f12:=diff(nablaf[1],y);f22:=diff(nablaf[2],y);
![]()
![]()
![]()
> H;
![_rtable[7759808]](images/harj769.gif)
> Hkrp:=<<(-1)^(m+1),0>|<0,(-1)^(n+1)>>;
![Hkrp := _rtable[7835484]](images/harj770.gif)
Matriisi on diagonaalimatriisi, joten tehtävä on valmiiksi pääakselimuodossa (ominaisarvot päälävistäjällä).
Päätelmät:
Koska näemme funktiosta suoraan, että -2 < = f(x,y) <= 2 ja paikalliset min/max-arvot ovat -2 ja 2, niin paikalliset ääriarvot ovat globaaleja koko R^2:ssa.
Pisteiden vuorottelu tasossa voidaan vaikka esittää matriisina, jossa 1 tarkoitta maksimia, -1 minimiä ja 0 satulapistettä.
> <<-1,0,-1>|<0,1,0>|<-1,0,-1>>;
![_rtable[7921280]](images/harj771.gif)
Keskimmäimmäinen 1 edustaa O:a (m ja n parillisia).
Matriisia vastaava pintakuva ja korkeuskäyräkuva:
> plot3d(f,x=-Pi..Pi,y=-Pi..Pi,axes=box,style=patchcontour);
![[Maple Plot]](images/harj772.gif)
> contourplot(f,x=-Pi..Pi,y=-Pi..Pi,axes=box);
![]()
> plot3d(f,x=-2*Pi..2*Pi,y=-2*Pi..2*Pi,axes=box,style=patchcontour);
![[Maple Plot]](images/harj774.gif)
Maple-ratkaisu
Edellä laskimme Maplella "käsin". Tyypillinen Mapleratkaisu voisi edetä seuraavaan tapaan:
> f:=cos(x)+cos(y);g:=Vector(grad(f,[x,y]));H:=Matrix(hessian(f,[x,y]));
![]()
Error, (in Vector) dimension parameter is required for this form of initializer
Error, (in Matrix) dimension parameters are required for this form of initializer
> KRP:=[x=0,y=0],[x=0,y=Pi],[x=Pi,y=0],[x=Pi,y=Pi];
![]()
Tämän teimme kuitenkin "käsin". Tässä on kaikki mahdollisuudet Hessen matriiseisksi:
> H1:=subs(KRP[1],H);H2:=subs(KRP[2],H);H3:=subs(KRP[3],H);H4:=subs(KRP[4],H);
![H1 := _rtable[7759808]](images/harj777.gif)
![H2 := _rtable[7759808]](images/harj778.gif)
![H3 := _rtable[7759808]](images/harj779.gif)
![H4 := _rtable[7759808]](images/harj780.gif)
Loppu, kuten "käsinlaskussa".
5 LV
Tilavuus: V.
Sivu- ja kansimateriaali: a mk/m^2
Pohjamateriaali: 2a mk/m^2
> restart:
> with(plottools);with(plots):
![]()
![]()
![]()
Warning, the name changecoords has been redefined
>
display(cuboid([0,0,0],[1,1,1])):
> x*y*z=V;
![]()
Kustannusfunktio: pohja*2a + (sivut+kansi)*a
> f:=(x,y,z)->x*y*2*a + (2*x*z+2*y*z+x*y)*a ;
>
![]()
Tilavuusehdon perusteella voidaan yksi muuttuja eliminoida:
> g:=simplify(f(x,y,V/(x*y)));
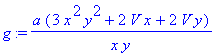
Tässä on siis minimoitava funktio (lauseke) joukossa x >0, y>0.
> dg1:=simplify(diff(g,x));
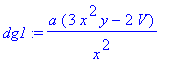
> dg2:=simplify(diff(g,y));
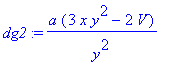
Käsin laskemalla saadaan vaivattomasti :
> xmin:=((2*V)/3)^(1/3); ymin:=xmin;
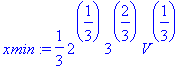
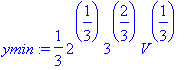
> zmin:=V/(xmin*ymin);
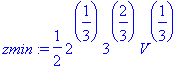
> minarvo:=f(xmin,ymin,zmin);
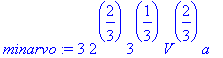
> g:=expand(g);
![]()
Olkoon vaikkapa a=1 ja V=5. (Periaatteessa tilanne on aivan sam. olivatpa arvot mitä tahansa (positiivisia).)
> a:=1: V:=5: g;
![]()
> minarvo;evalf(%);
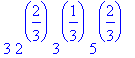
![]()
>
> display(plot([20/(3*x),0.5],x=0.5..12,color=red),plot([[0.5,12],[0.5,0.5],[0.5,3/0.5]],x=0.5..6),plot([[xmin,ymin]],style=point,symbol=cross,symbolsize=20,color=black),view=[0..12,0..12]);
![[Maple Plot]](images/harj797.gif)
Tässä suljetussa ja rajoitetussa joukossa jatkuva funktio g saa miniminsä. Reunalla se ei sitä saa, koska kaikissa reunapisteissä funktion arvo on suuremp kuin "ristipisteessä", joka on KRP ja niin ollen ainoa mahdollinen minimipiste
ja näinollen minimipiste.
Punaisen alueen ulkopuolella g on kaikkialla vieläkin suurempi, joten "ristipiste" on globaali minimi koko joukossa
x>0, y>0 (avoimessa 1. koordinaattoneljänneksessä).
>
> solve({dg1=0,dg2=0},{x,y});
![]()
> map(allvalues,%);
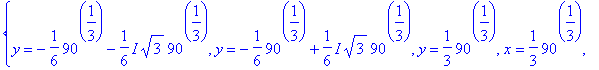
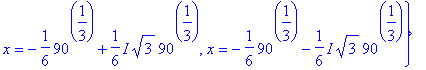
Luentotehtäviin liittyvää
> F:=1/x+1/y+x*y;plot3d(F,x=1/3..3,y=1/3..3/x,style=patchcontour);
>
![]()
![[Maple Plot]](images/harj7102.gif)
> A:=Matrix([[17,6],[6,8]]);
![A := _rtable[8193908]](images/harj7103.gif)
> eigenvectors(A);
![eigenvectors(_rtable[8193908])](images/harj7104.gif)
> display(plot(16/x^2,x=2..4),contourplot(x^2+y^2,x=0..4,y=0..16,contours=[6,7,8,9,10,11,12,13,15],color=blue),scaling=constrained);
![[Maple Plot]](images/harj7105.gif)
>