Kirjallisuutta

• []

Materiaalia

Funktion arvojen vertailuun perustuvia menetelmiä

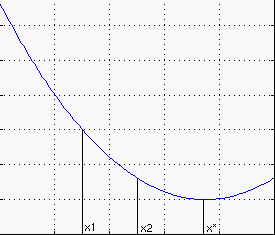
Harjoitellaan samalla Matlab-kuvaa. Huomaa, että uudessa Matlabin versiossa 5.3 voidaan funktio määritellä myös suoraan istunnossa inline -komennon avulla. Kuvassa olevat pystyviivat ja tekstit on tehty Matlabin kuvaeditorilla.

>> f=inline('.3+(x-3/4).^2','x'); >> fplot(f,[0 1]) >> %ylim([0 1.6]) >> grid

Maar. f:[a,b] -> R on unimodaalinen (yksihuippuinen), jos on olemassa yksikäs x^* välillä [a,b] siten, että vasemmalla puolella pienenee ja oikealla kasvaa.

Periaate

Fibonacci-haku

Matlab-toteutus

%%%%%%%% Tiedosto fib.m %%%%%%%%%%%%%%
function F=fib(n)
F(1)=1;F(2)=1;
for i=2:n-1 F(i+1)=F(i-1)+F(i);end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%% Skripti fibhaku.m %%%%%%%%%%%
clf
a(1)=-3;b(1)=5;
n=10;
F=fib(n);

for i=1:n-2

  L(i)=b(i)-a(i);patka=(F(n-(i+1))/F(n))*L(1);
  x0(i)=a(i)+patka;x1(i)=b(i)-patka;
  f0=f(x0(i));f1=f(x1(i));
   if (f0 < f1)
     b(i+1)=x1(i); a(i+1)=a(i);
   elseif (f0 > f1)
     a(i+1)=x0(i); b(i+1)=b(i);
   else
     a(i+1)=x0(i); b(i+1)=x1(i); 

   end;

  plot([a(i)  b(i)],0.2*[1-i 1-i ],'or')
  axis([a(1)-.2 b(1)+.2 -2 1])
  hold on
  plot([a(i)  b(i)],0.2*[1-i 1-i ],'k')
  plot([x0(i)  x1(i)],0.2*[1-i 1-i ],'*b')

  if i<6
     text(a(i)+0.05,0.2*(1-i+0.1),['a(',num2str(i),')'])
     text(b(i)+0.05,0.2*(1-i+0.1),['b(',num2str(i),')'])
  end;

end;

taulukko=[a(1:n-2)' b(1:n-2)' x0' x1' f(x0)' f(x1)']
fplot(f,[a(1) b(1)])
grid
title('Fibonacci-haku')
%%%%%%%%%%%%%%% fibhaku.m loppui %%%%%%%%%%%%%%%%%%%

Ajon tulos:

      a         b          x0        x1       f(x0)    f(x1)

   -3.0000    5.0000    0.0545    1.9455    0.1121    7.6757
   -3.0000    1.9455   -1.1091    0.0545   -0.9881    0.1121
   -3.0000    0.0545   -1.8364   -1.1091   -0.3005   -0.9881
   -1.8364    0.0545   -1.1091   -0.6727   -0.9881   -0.8929
   -1.8364   -0.6727   -1.4000   -1.1091   -0.8400   -0.9881
   -1.4000   -0.6727   -1.1091   -0.9636   -0.9881   -0.9987
   -1.1091   -0.6727   -0.9636   -0.8182   -0.9987   -0.9669
   -1.1091   -0.8182   -0.9636   -0.9636   -0.9987   -0.9987

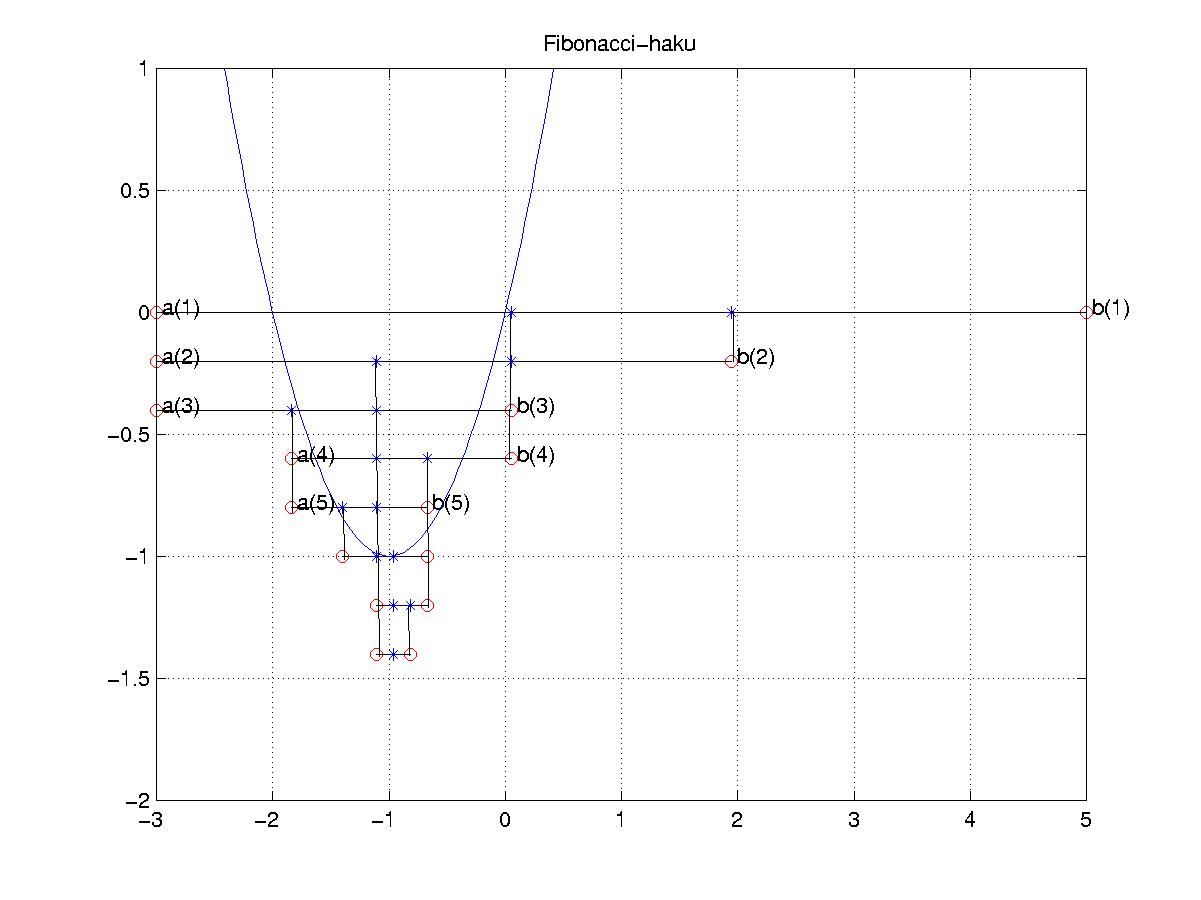
Kuvan pystyviivat editoitiin Matlabin kuvaeditorilla.

Interpolaatioon perustuvia menetelmiä

Hybridimenetelmät

Luku4

Kotiin