Seosprobleema (P3/K3)
| > |
with(LinearAlgebra):with(linalg):
|
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
| > |
A:=<<-1/10,1/10>|<3/40,-1/5>>;
|
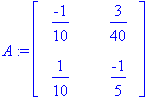
| > |
(lambda,ov):=Eigenvectors(A);
|
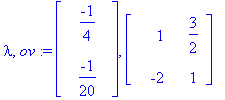
| > |
x:=[ov[1..-1,1],ov[1..-1,2]];
|
![x := [Vector(%id = 16314156), Vector(%id = 16270020)]](images/odemaple3.gif)
| > |
Yh:=C1*exp(lambda[1]*t)*x[1]+C2*exp(lambda[2]*t)*x[2];
|
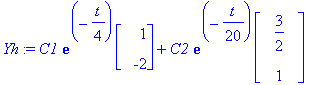
HY-yrite: Yksinkertaisinta on yrittää vakiovektoria y=v;
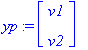
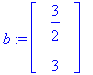
| > |
map(diff,yp,t)='A.yp'+b;
|
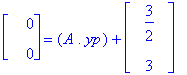
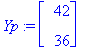
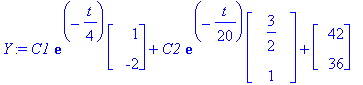
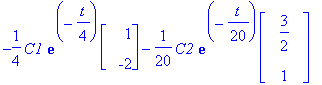
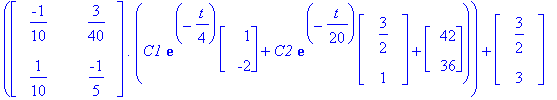
Tarkistaminen vektorimuodossa ei käykään helposti, Maplen tietorakenteet tekevät tenän.
No, jatketaan ja jätetään tarkistus loppuun.
| > |
AE:=subs(t=0,Y)=<25,15>;AE:=map(eval,%);
|
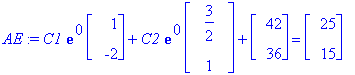
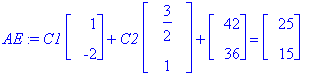
![vector([C1+3/2*C2+42, -2*C1+C2+36])](images/odemaple14.gif)
| > |
Ceet:=LinearSolve(<<1,-2>|<3/2,1>>,<25-42,15-36>);
|
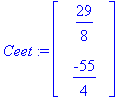
| > |
Y:=subs(C1=Ceet[1],C2=Ceet[2],Y);
|
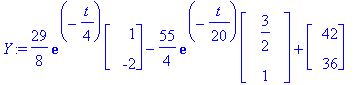
![y12 := vector([29/8*exp(-1/4*t)-165/8*exp(-1/20*t)+42, -29/4*exp(-1/4*t)-55/4*exp(-1/20*t)+36])](images/odemaple17.gif)
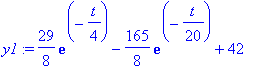
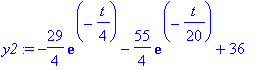
| > |
plot([y1,y2],t=0..100);
|
![[Maple Plot]](images/odemaple20.gif)
| > |
<diff(y1,t),diff(y2,t)>;
|
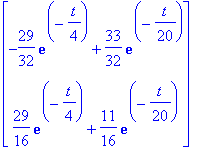
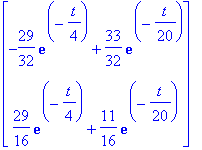
Kävihän se tarkistus toki näin!
2x2-systeemejä, faasitasoja
Katsotaan ensin, mikä on "aikatason" ja faasitason suhde ja mikä on vastaava Maple-syntaksi.
Merkitään havainnollisuuden vuoksi faasitason pisteitä (x(t) , y(t)).
Olk.
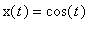 ,
,
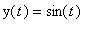 .
.
| > |
plot([x,y],t=0..2*Pi,title="Aikakuva"); # Käyräparvi
|
![[Maple Plot]](images/odemaple25.gif)
| > |
plot([x,y,t=0..2*Pi],title="Faasikuva"); # Parametrikäyrä tasossa
|
![[Maple Plot]](images/odemaple26.gif)
Esim. 1 (KRE s. 163)
| > |
restart: with(LinearAlgebra): with(linalg): with(plots):
|
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
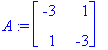
| > |
(lambda,ov):=Eigenvectors(A);
|
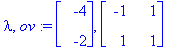
| > |
x1:=ov[1..-1,1]; x2:=ov[1..-1,2];
|
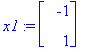
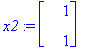
| > |
Y:=C1*exp(lambda[1]*t)*x1+C2*exp(lambda[2]*t)*x2;
|
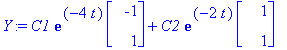
| > |
C1:=1: C2:=.5: plot([Y[1],Y[2]],t=0..2,title="Ratkaisufunktiot y1(t)ja y2(t) aikakuvassa",color=[red,blue]);
|
![[Maple Plot]](images/odemaple32.gif)
Faasikuvan piirtämistä ajatellen kannattaa katsoa taas ominaisvektorikantaa, Sekä käsin, että Maplella on helpompaa, jos otetaan käyräparametriksi
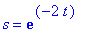
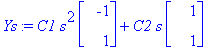
![YY := vector([-C1*s^2+C2*s, C1*s^2+C2*s])](images/odemaple35.gif)
| > |
C1:=arvo1: C2:=arvo2: 'plot'([YY[1],YY[2],s=a..b]); # Huomaa param. piirron syntaksi!
|
![plot([-arvo1*s^2+arvo2*s, arvo1*s^2+arvo2*s, s = a .. b])](images/odemaple36.gif)
| > |
C1:=-2: C2:=1: plot([YY[1],YY[2],s=0..1]);kuva1:=%:
|
![[Maple Plot]](images/odemaple37.gif)
| > |
C1:=2: C2:=-1: kuva2:=plot([YY[1],YY[2],s=0..1]):
|
![[Maple Plot]](images/odemaple38.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],s=0..1],C2=-2..2),C1=-2..2);
|
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/odemaple39.gif)
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/odemaple40.gif)
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/odemaple41.gif)
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/odemaple42.gif)
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/odemaple43.gif)
![parvi := [2*s^2-2*s, -2*s^2-2*s, s = 0 .. 1], [2*s^2-s, -2*s^2-s, s = 0 .. 1], [2*s^2, -2*s^2, s = 0 .. 1], [2*s^2+s, -2*s^2+s, s = 0 .. 1], [2*s^2+2*s, -2*s^2+2*s, s = 0 .. 1], [s^2-2*s, -s^2-2*s, s =...](images/odemaple44.gif)
![[Maple Plot]](images/odemaple45.gif)
| > |
display(%,arrow([x1,x2]));
|
![[Maple Plot]](images/odemaple46.gif)
Warning, the name adjoint has been redefined
| > |
DEplot([D(y1)(t)=-3*y1(t)+y2(t),D(y2)(t)=y1(t)-3*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-4..4,y2=-4..4,color=grey);
|
![[Maple Plot]](images/odemaple47.gif)
| > |
display(kuva,%,title="Trajektoreita ja suuntakenttä");
|
![[Maple Plot]](images/odemaple48.gif)
1. 2x2-faasitasotyypit
KRE:ssä on perusesimerkkejä ss. 164 - 168.
Käydään tässä EN:n sivujen mukaan ja käytetään EN-nimityksiä
[EN]: Eirola-Nevanlinna: Diff. yht. sys. L3-luentoja
1.1 Esim. 2.2 Lähde, ominaisarvot > 0
| > |
restart: with(LinearAlgebra): with(linalg): with(plots):
|
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
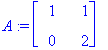
| > |
(lambda,ov):=Eigenvectors(A);
|
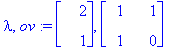
| > |
v1:=ov[1..-1,1]; v2:=ov[1..-1,2];
|
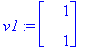
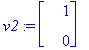
| > |
y:=t->C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
![y := proc (t) options operator, arrow; C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2 end proc](images/odemaple53.gif)
| > |
Y:=y(t); # Vektorilauseke.
|
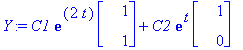
| > |
C1:=1: C2:=.5: plot([Y[1],Y[2]],t=0..2,title="Ratkaisufunktiot y1(t)ja y2(t) aikakuvassa",color=[red,blue]);
|
![[Maple Plot]](images/odemaple55.gif)
| > |
Ys:=map(eval,subs(t=log(s),y(t)));
|
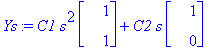
![YY := vector([C1*s^2+C2*s, C1*s^2])](images/odemaple57.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],s=0..4],C2=-2..2),C1=-2..2):
|
| > |
parvi: # Vaihda puolipiste, niin näet "parven".
|
![[Maple Plot]](images/odemaple58.gif)
| > |
display(%,arrow([v1,v2]),view=[-5..5,-5..5]);
|
![[Maple Plot]](images/odemaple59.gif)
Warning, the name adjoint has been redefined
| > |
DEplot([diff(y1(t),t)=y1(t)+y2(t),diff(y2(t),t)=2*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey);
|
![[Maple Plot]](images/odemaple60.gif)
| > |
display(kuva,%,title="Lähde,lambda[1] > 0, lambda[2] > 0");
|
![[Maple Plot]](images/odemaple61.gif)
1.2 Esim. 2.3, Nielu, ominaisarvot < 0
Periaatteessa samanlainen kuin lähde edellä, mutta nyt ominaisarvot negatiiviset. Trajektirit virtaavat origoon.
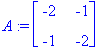
| > |
(lambda,ov):=Eigenvectors(A);
|
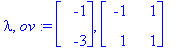
| > |
v1:=ov[1..-1,1]; v2:=ov[1..-1,2];
|
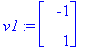
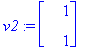
| > |
y:=t->C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
![y := proc (t) options operator, arrow; C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2 end proc](images/odemaple66.gif)
| > |
subs(t=log(s),y(t)): Ys:=eval(%); # Siirrytään logaritmiseen parametriin. Tämä ei ole välttämätöntä, mutta helpottaa erit. käsin piirtoa, myös Maple-piirrossa skaala pysyy paremmin hanskassa.
|
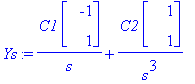
| > |
# 0 < s < 1, kun t > 0.
|
Lasketaan koordinaattimuodossa:
![YY := vector([-C1/s+C2/s^3, C1/s+C2/s^3])](images/odemaple68.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],s=0..4],C2=-2..2),C1=-2..2):
|
![[Maple Plot]](images/odemaple69.gif)
| > |
display(%,arrow([v1,v2]),view=[-5..5,-5..5]);
|
![[Maple Plot]](images/odemaple70.gif)
| > |
display(kuva,DEplot([D(y1)(t)=-2*y1(t)-y2(t),D(y2)(t)=-y1(t)-2*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey),title="Nielu");
|
![[Maple Plot]](images/odemaple71.gif)
Nielu on vahvasti stabiili. Kaikki trajektorit lähestyvät O:a, kun t ->
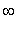 .
.
1.3 Esim 2.4 Satula, reaaliset, erimerkk.
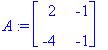
| > |
(lambda,ov):=Eigenvectors(A);
|
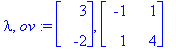
| > |
v1:=ov[1..-1,1]; v2:=ov[1..-1,2];
|
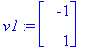
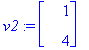
| > |
Y:=C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
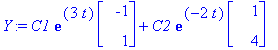
| > |
subs(t=log(s),Y);Ys:=eval(%);
|
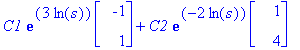
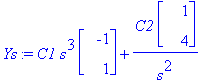
![YY := vector([-C1*s^3+C2/s^2, C1*s^3+4*C2/s^2])](images/odemaple80.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],s=0..4],C2=-2..2),C1=-2..2):
|
![[Maple Plot]](images/odemaple81.gif)
| > |
display(%,arrow([v1,v2]),view=[-5..5,-5..5]);
|
![[Maple Plot]](images/odemaple82.gif)
| > |
display(kuva,DEplot([D(y1)(t)=2*y1(t)-y2(t),D(y2)(t)=-4*y1(t)-y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey),title="Satula");
|
![[Maple Plot]](images/odemaple83.gif)
Epästabiili.
Osa trajektoreista -->
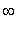 , lähdettiinpä miten läheltä O:a tahansa (erit. posit. ominaisarvoa vastaavan
, lähdettiinpä miten läheltä O:a tahansa (erit. posit. ominaisarvoa vastaavan
ominaisvektorin pisteistä).
1.4 Esim. 2.5, epästabiili fokus , kompleksiset, Re(
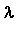 ) > 0
) > 0
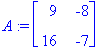
| > |
(lambda,ov):=Eigenvectors(A);
|
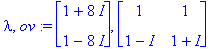
| > |
v1:=ov[1..-1,1]; v2:=ov[1..-1,2];
|
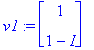
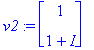
| > |
Y:=C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
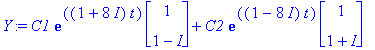
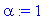
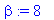
| > |
u:=map(Re,v1); v:=map(Im,v1);
|
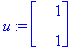
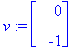
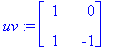
| > |
C:=<<cos(beta*t),-sin(beta*t)>|<sin(beta*t),cos(beta*t)>>;
|
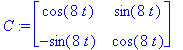
| > |
Y:=exp(alpha*t)*(uv.C.<C1,C2>); # Sulut laitettava näin, Maple ei täysin hallitse kertolaskujen liitännäisyyttä.
|
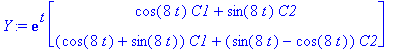
![YY := vector([exp(t)*(cos(8*t)*C1+sin(8*t)*C2), exp(t)*((cos(8*t)+sin(8*t))*C1+(sin(8*t)-cos(8*t))*C2)])](images/odemaple98.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],t=0..2],C2=-2..2),C1=-2..2):
|
![[Maple Plot]](images/odemaple99.gif)
| > |
display(%,arrow([u,v]),view=[-5..5,-5..5]);
|
![[Maple Plot]](images/odemaple100.gif)
| > |
display(kuva,DEplot([D(y1)(t)=9*y1(t)-8*y2(t),D(y2)(t)=16*y1(t)-7*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey),title="Epästabiili fokus");
|
![[Maple Plot]](images/odemaple101.gif)
1.5 Esim. 3.0 Degeneroitununut lähde (KRE s. 168)
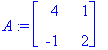
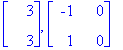
| > |
expA:=t->exp(3*t)*<<1+t,-t>|<t,1-t>>;
|
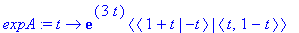
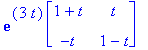
| > |
exponential(A,t); # Tarkistus.
|
![matrix([[exp(3*t)+t*exp(3*t), t*exp(3*t)], [-t*exp(3*t), exp(3*t)-t*exp(3*t)]])](images/odemaple106.gif)
| > |
Y:=exp(3*t)*((expA(t)/exp(3*t)).<C1,C2>);
|
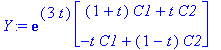
Jälleen piti temppuilla, koska kertolaskun liitännäisyys ei ole ihan hallinnassa.
![YY := vector([exp(3*t)*((1+t)*C1+t*C2), exp(3*t)*(-t*C1+(1-t)*C2)])](images/odemaple108.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],t=-2..2],C2=-2..2),C1=-2..2):
|
| > |
display(plot([parvi]),arrow(<-1,1>),view=[-5..5,-5..5],title="Degeneroitunut lähde");
|
![[Maple Plot]](images/odemaple109.gif)
EHY-esim, degeneroitunut
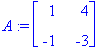
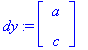
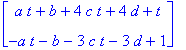
2. Diffyhtsys, analyyttisesti, numeerisesti, graafisesti, dsolve,dsolve(...,numeric), DEplot
Edellä käytimme piirtoon analyyttisiä ratkaisuja, jotka lineaariselle systeemille ovat saatavissa.
o
dsolve
osaa suoraan ratkaista analyyttisesti, tosin edellä tehty on varmasti opettavaisempaa.
Warning, premature end of input
Maple-tekniikan suhteen analyyttisen ratkaisun alla oleva jatkokäsittely on opettavaista ja johdattelee vastaavaan numeeristen menetelmien kohdalla.
Trajektorien piirto voidaan suorittaa myös
DEplot
:lla, joka kuitenkin on varsin karkea väline. (Laskee kiinteällä askelpituudella.) Katsotaan sitäkin joka tapauksessa.
Yleisessä, epälineaarisessa tapauksessa käytetään numeerista ratkaisijaa laskemiseen. (Niin teemme aina Matlabissa.)
Määrittelemällä sopivasti apufunktioita, saamme homman oikein joustavaksi.
Nämä ideat ovat peräisin kirjasta [Coombes & al.]
2.1 Analyyttinen ratkaisu (dsolve)
Esimerkki:
| > |
AAteht:={diff(x(t),t)=x(t)+2*y(t),diff(y(t),t)=-x(t),x(0)=a,y(0)=0};
|
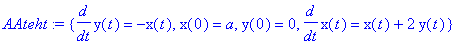
| > |
aaratk:=dsolve(AAteht,{x(t),y(t)});
|
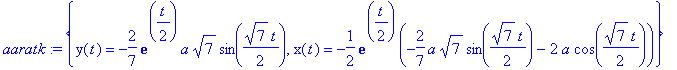
| > |
aaratkf:=unapply(subs(aaratk,[x(t),y(t),t=trange]),a,trange);
|
![aaratkf := proc (a, trange) options operator, arrow; [-1/2*exp(1/2*t)*(-2/7*a*7^(1/2)*sin(1/2*7^(1/2)*t)-2*a*cos(1/2*7^(1/2)*t)), -2/7*exp(1/2*t)*a*7^(1/2)*sin(1/2*7^(1/2)*t), t = trange] end proc](images/odemaple117.gif)
![[-1/2*exp(1/2*t)*(-4/7*sin(1/2*7^(1/2)*t)*7^(1/2)-4*cos(1/2*7^(1/2)*t)), -4/7*exp(1/2*t)*7^(1/2)*sin(1/2*7^(1/2)*t), t = a .. b]](images/odemaple118.gif)
| > |
plot(aaratkf(1,0..10)):
|
| > |
seq(aaratkf(a,0..10),a=-1..1);
|
![[-1/2*exp(1/2*t)*(2/7*sin(1/2*7^(1/2)*t)*7^(1/2)+2*cos(1/2*7^(1/2)*t)), 2/7*exp(1/2*t)*7^(1/2)*sin(1/2*7^(1/2)*t), t = 0 .. 10], [0, 0, t = 0 .. 10], [-1/2*exp(1/2*t)*(-2/7*sin(1/2*7^(1/2)*t)*7^(1/2)-2...](images/odemaple119.gif)
![[-1/2*exp(1/2*t)*(2/7*sin(1/2*7^(1/2)*t)*7^(1/2)+2*cos(1/2*7^(1/2)*t)), 2/7*exp(1/2*t)*7^(1/2)*sin(1/2*7^(1/2)*t), t = 0 .. 10], [0, 0, t = 0 .. 10], [-1/2*exp(1/2*t)*(-2/7*sin(1/2*7^(1/2)*t)*7^(1/2)-2...](images/odemaple120.gif)
| > |
plot([seq(aaratkf(a,-4..3),a=-4..4)]);
|
![[Maple Plot]](images/odemaple121.gif)
Tehdään käyttäjälle vielä helpommaksi uudella kertakäyttöfunktiolla
| > |
faasi:=trange->plot([seq(aaratkf(a,trange),a=-4..4)]);
|
![faasi := proc (trange) options operator, arrow; plot([seq(aaratkf(a,trange),a = -4 .. 4)]) end proc](images/odemaple122.gif)
| > |
faasi(-4..3);faasi(-10..1);
|
![[Maple Plot]](images/odemaple123.gif)
![[Maple Plot]](images/odemaple124.gif)
Vaihdetaan parametriväliä, lisätään samalla funktioon mahdollisuus antaa plot-optioita.
| > |
faasi:=(trange,opt1,opt2)->plot([seq(aaratkf(a,trange),a=-20..20)],opt1,opt2);
|
![faasi := proc (trange, opt1, opt2) options operator, arrow; plot([seq(aaratkf(a,trange),a = -20 .. 20)],opt1,opt2) end proc](images/odemaple125.gif)
| > |
faasi(-10..10,view=[-10..10,-10..10],numpoints=200);
|
![[Maple Plot]](images/odemaple126.gif)
-
Käyttöohje:
-
Aina, kun haluat vaihtaa parametriväliä, suorita määrittelyrivi
faasi:=(..)->..
uudestaan.
-
Kun piirrät eri
t:
n arvoilla, suorita komento
faasi(..)
;
-
Kun vaihdat diffyhtsysteemiä, suorita ensin rivit:
AAteht:=..
ja
aaratk:= ..
.
Error, `..` unexpected
2.2. Numeerinen ratkaisu (dsolve(..,numeric))
s. 170-..
Teknisesti asia voitaisiin ajatella hoidettavaksi aivan samoin kuin yllä, lisäämällä dsolve-komentoon valitsin "
numeric
".
Tämä ei kuitenkaan toimi yllä olevalla tavalla tehtynä, koska
dsolve(...,numeric)
tarvitsee numeeriset alkuarvot, ennenkuin se voi laskea mitään. Nyt täytyy olla senverran ovela, että
estetään Maple evaluoimasta
mitään
ennen numeeristen alkuarvojen
antamista.
Nämä ovat hiukan sofistikoituneita symbolilaskenta-asioita. Jos haluat pitäytyä vain ylimalkaisessa evalointiärjestysasioiden ymmärryksessä, voit toki ottaa tämän työarkin kaikelle tämänsuunaiselle toiminnalle pohjaksi.
Warning, the name changecoords has been redefined
| > |
dys:=diff(x(t),t)=x(t)+2*y(t),diff(y(t),t)=-x(t);
|
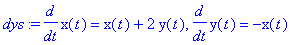
| > |
numratk:=(a,b)->dsolve({dys,x(0)=a,y(0)=b},{x(t),y(t)},numeric,maxfun=1000);
|
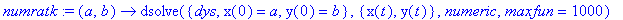
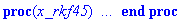
| > |
numratk(0,1)(1); # Numeerisen ratkaisun arvo annetussa pisteessä.
|
![[t = 1., x(t) = 2.41641902799175812, y(t) = -.199526923222372004]](images/odemaple130.gif)
Nyt käytetään
->
määrittelyä, jolloin evaluointi tapahtuu vasta suoritusaikana. Voit kokeilla, mitä tapahtuu
unapply
-tyylillä, jos haluat nähdä, mikä on virheilmoitus.
Error, `->` unexpected
| > |
kayra:=(a,b,trange)->odeplot(numratk(a,b),[x(t),y(t)],trange);
|
![kayra := proc (a, b, trange) options operator, arrow; odeplot(numratk(a,b),[x(t), y(t)],trange) end proc](images/odemaple131.gif)
Tämä on yhtä looginen kuin
odeplot:n
syntaksi. Siinä noudatetaan funktioplot:n syntaksia (x(t) ja y(t) nyt eivät ihan näytä funktioilta, mutta tämän lähemmäksi rautaista logiikkaa ei näköjään
odeplot:
ssa ole päästy.)
Error, missing operator or `;`
![[Maple Plot]](images/odemaple132.gif)
| > |
numfaasi:=trange->display([seq(seq(kayra(a,b,trange),a=-2..2),b=-2..2)],view=[-20..20,-15..15]);
|
![numfaasi := proc (trange) options operator, arrow; display([seq(seq(kayra(a,b,trange),a = -2 .. 2),b = -2 .. 2)],view = [-20 .. 20, -15 .. 15]) end proc](images/odemaple133.gif)
![[Maple Plot]](images/odemaple134.gif)
Hienosti nämä toimivat, kun ne näin rakennetaan!
Tästä on sopivaa jatkaa aluksi vaikka muodostamalla lineaaristen faasitasot.
Nyt voi kuvaan lisätä trajektoreita yksi kerrallaan paljon tarkemmin kuin DEplot:lla, jolla kannattaa tehdä vain suuntakenttä. (Alla on esitetty kätevä tapa DEplot-käyttöön, mutta kuvat eivät ole kauniita paksuine viivoineen.
Alla on esietty konkreettisesti, miten homma käy.
Tietysti kannattaa verrata
Matlab
-tyyliin. Se voidaan rakentaa eri tavalla vuorovaikutteiseksi.
2.3 Graafinen, DEplot ja dsolve(..,numeric) yhdessä
| > |
with(DEtools):with(plots):
|
Warning, the name changecoords has been redefined
| > |
dys:=diff(x(t),t)=x(t)+2*y(t),diff(y(t),t)=-x(t);
|
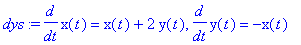
| > |
AA:=[seq(seq([0,a,b],a=-2..2),b=-2..2)];
|
![AA := [[0, -2, -2], [0, -1, -2], [0, 0, -2], [0, 1, -2], [0, 2, -2], [0, -2, -1], [0, -1, -1], [0, 0, -1], [0, 1, -1], [0, 2, -1], [0, -2, 0], [0, -1, 0], [0, 0, 0], [0, 1, 0], [0, 2, 0], [0, -2, 1], [...](images/odemaple136.gif)
![AA := [[0, -2, -2], [0, -1, -2], [0, 0, -2], [0, 1, -2], [0, 2, -2], [0, -2, -1], [0, -1, -1], [0, 0, -1], [0, 1, -1], [0, 2, -1], [0, -2, 0], [0, -1, 0], [0, 0, 0], [0, 1, 0], [0, 2, 0], [0, -2, 1], [...](images/odemaple137.gif)
| > |
faasitaso:=trange->DEplot([dys],[x(t),y(t)],t=trange,AA,stepsize=0.1);
|
![faasitaso := proc (trange) options operator, arrow; DEplot([dys],[x(t), y(t)],t = trange,AA,stepsize = .1) end proc](images/odemaple138.gif)
![[Maple Plot]](images/odemaple139.gif)
| > |
DEplot([dys],[x(t),y(t)],t=-3..3,x=-3..3,y=-3..3,stepsize=0.1);
|
![[Maple Plot]](images/odemaple140.gif)
| > |
proc (trange) options operator, arrow; DEplot(dys,[x(t), y(t)],t = trange,AA,stepsize = .1) end proc
|
Warning, premature end of input
| > |
DEplot([diff(y1(t),t)=y1(t)+y2(t),diff(y2(t),t)=2*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey);
|
![[Maple Plot]](images/odemaple141.gif)
| > |
numratk:=(a,b)->dsolve({dys,x(0)=a,y(0)=b},{x(t),y(t)},numeric,maxfun=1000);
|
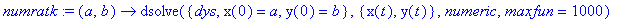
| > |
kayra:=(a,b,trange)->odeplot(numratk(a,b),[x(t),y(t)],trange);
|
![kayra := proc (a, b, trange) options operator, arrow; odeplot(numratk(a,b),[x(t), y(t)],trange) end proc](images/odemaple143.gif)
| > |
numfaasi:=trange->display([seq(seq(kayra(a,b,trange),a=-2..2),b=-2..2)]);
|
![numfaasi := proc (trange) options operator, arrow; display([seq(seq(kayra(a,b,trange),a = -2 .. 2),b = -2 .. 2)]) end proc](images/odemaple144.gif)
| > |
suuntak:=DEplot([dys],[x(t),y(t)],t=-3..3,x=-3..3,y=-3..3,stepsize=0.1,color=grey):
|
| > |
display([numfaasi(-3..3),suuntak]);
|
![[Maple Plot]](images/odemaple145.gif)
| > |
display(suuntak,kayra(0,1.8,-3..3));
|
![[Maple Plot]](images/odemaple146.gif)
Tällä tavalla on aika kätevää rakentaa faasikuvaa:
- Klikkaa hiirellä kuvaan ja lue koordinaatit vasemmasta ylänurkasta.
- Jatka kuvan rakentelua yllä olevalla
display
-tyylillä.
Warning, premature end of input
| > |
display(%,kayra(-0.7,1.1,-3..3));
|
![[Maple Plot]](images/odemaple147.gif)
![[Maple Plot]](images/odemaple148.gif)
| > |
aasi:=(trange,opt1,opt2)->plot([seq(aaratkf(a,trange),a=-20..20)],opt1,opt2);
|
![aasi := proc (trange, opt1, opt2) options operator, arrow; plot([seq(aaratkf(a,trange),a = -20 .. 20)],opt1,opt2) end proc](images/odemaple149.gif)
![proc (trange, opt1, opt2) options operator, arrow; plot([seq(aaratkf(a,trange),a = -20 .. 20)],opt1,opt2) end proc](images/odemaple150.gif)
| > |
proc (trange, opt1, opt2) options operator, arrow; plot([seq(aaratkf(a,trange),a = -20 .. 20)],opt1,opt2) end proc;
|
![proc (trange, opt1, opt2) options operator, arrow; plot([seq(aaratkf(a,trange),a = -20 .. 20)],opt1,opt2) end proc](images/odemaple151.gif)
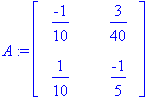
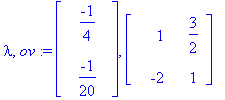
![x := [Vector(%id = 16314156), Vector(%id = 16270020)]](images/odemaple3.gif)
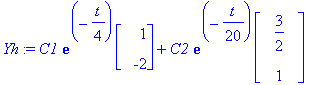
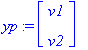
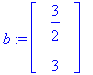
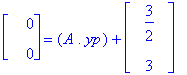
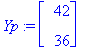
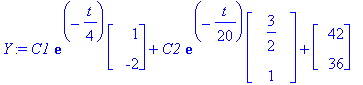
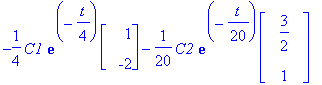
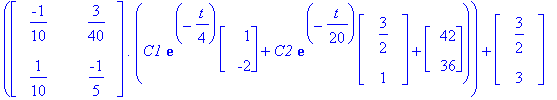
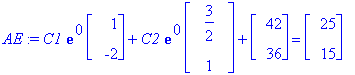
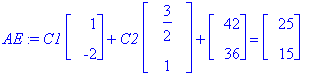
![]()
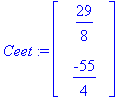
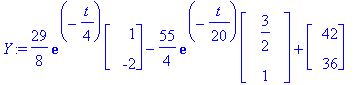
![y12 := vector([29/8*exp(-1/4*t)-165/8*exp(-1/20*t)+42, -29/4*exp(-1/4*t)-55/4*exp(-1/20*t)+36])](images/odemaple17.gif)
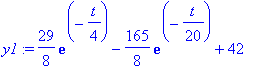
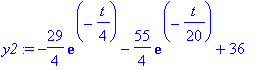
![[Maple Plot]](images/odemaple20.gif)
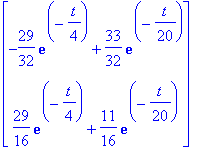
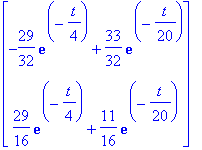
![[Maple Plot]](images/odemaple25.gif)
![[Maple Plot]](images/odemaple26.gif)
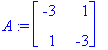
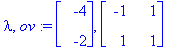
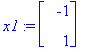
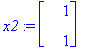
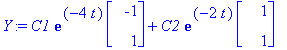
![[Maple Plot]](images/odemaple32.gif)
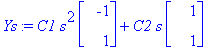
![[Maple Plot]](images/odemaple37.gif)
![[Maple Plot]](images/odemaple38.gif)
![[Maple Plot]](images/odemaple45.gif)
![[Maple Plot]](images/odemaple46.gif)
![[Maple Plot]](images/odemaple47.gif)
![[Maple Plot]](images/odemaple48.gif)
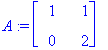
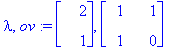
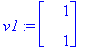
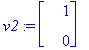
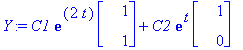
![[Maple Plot]](images/odemaple55.gif)
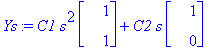
![[Maple Plot]](images/odemaple58.gif)
![[Maple Plot]](images/odemaple59.gif)
![[Maple Plot]](images/odemaple60.gif)
![[Maple Plot]](images/odemaple61.gif)
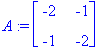
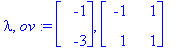
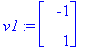
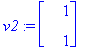
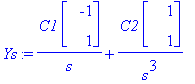
![YY := vector([-C1/s+C2/s^3, C1/s+C2/s^3])](images/odemaple68.gif)
![[Maple Plot]](images/odemaple69.gif)
![[Maple Plot]](images/odemaple70.gif)
![[Maple Plot]](images/odemaple71.gif)
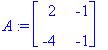
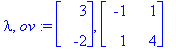
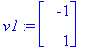
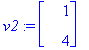
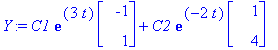
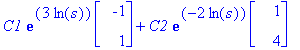
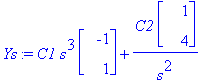
![YY := vector([-C1*s^3+C2/s^2, C1*s^3+4*C2/s^2])](images/odemaple80.gif)
![[Maple Plot]](images/odemaple81.gif)
![[Maple Plot]](images/odemaple82.gif)
![[Maple Plot]](images/odemaple83.gif)
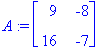
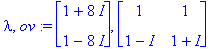
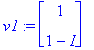
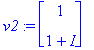
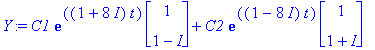
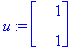
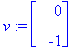
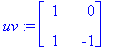
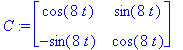
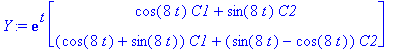
![[Maple Plot]](images/odemaple99.gif)
![[Maple Plot]](images/odemaple100.gif)
![[Maple Plot]](images/odemaple101.gif)
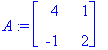
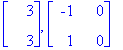
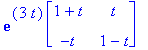
![matrix([[exp(3*t)+t*exp(3*t), t*exp(3*t)], [-t*exp(3*t), exp(3*t)-t*exp(3*t)]])](images/odemaple106.gif)
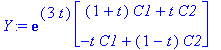
![[Maple Plot]](images/odemaple109.gif)
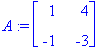
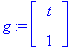
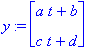
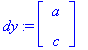
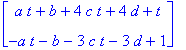
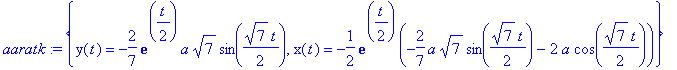
![aaratkf := proc (a, trange) options operator, arrow; [-1/2*exp(1/2*t)*(-2/7*a*7^(1/2)*sin(1/2*7^(1/2)*t)-2*a*cos(1/2*7^(1/2)*t)), -2/7*exp(1/2*t)*a*7^(1/2)*sin(1/2*7^(1/2)*t), t = trange] end proc](images/odemaple117.gif)
![[-1/2*exp(1/2*t)*(-4/7*sin(1/2*7^(1/2)*t)*7^(1/2)-4*cos(1/2*7^(1/2)*t)), -4/7*exp(1/2*t)*7^(1/2)*sin(1/2*7^(1/2)*t), t = a .. b]](images/odemaple118.gif)
![[-1/2*exp(1/2*t)*(2/7*sin(1/2*7^(1/2)*t)*7^(1/2)+2*cos(1/2*7^(1/2)*t)), 2/7*exp(1/2*t)*7^(1/2)*sin(1/2*7^(1/2)*t), t = 0 .. 10], [0, 0, t = 0 .. 10], [-1/2*exp(1/2*t)*(-2/7*sin(1/2*7^(1/2)*t)*7^(1/2)-2...](images/odemaple119.gif)
![[-1/2*exp(1/2*t)*(2/7*sin(1/2*7^(1/2)*t)*7^(1/2)+2*cos(1/2*7^(1/2)*t)), 2/7*exp(1/2*t)*7^(1/2)*sin(1/2*7^(1/2)*t), t = 0 .. 10], [0, 0, t = 0 .. 10], [-1/2*exp(1/2*t)*(-2/7*sin(1/2*7^(1/2)*t)*7^(1/2)-2...](images/odemaple120.gif)
![[Maple Plot]](images/odemaple121.gif)
![[Maple Plot]](images/odemaple123.gif)
![[Maple Plot]](images/odemaple124.gif)
![[Maple Plot]](images/odemaple126.gif)
![[Maple Plot]](images/odemaple132.gif)
![[Maple Plot]](images/odemaple134.gif)
![[Maple Plot]](images/odemaple139.gif)
![[Maple Plot]](images/odemaple140.gif)
![[Maple Plot]](images/odemaple141.gif)
![[Maple Plot]](images/odemaple145.gif)
![[Maple Plot]](images/odemaple146.gif)
![[Maple Plot]](images/odemaple147.gif)
![[Maple Plot]](images/odemaple148.gif)