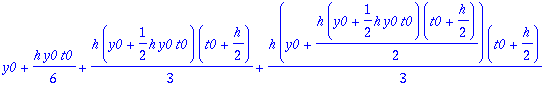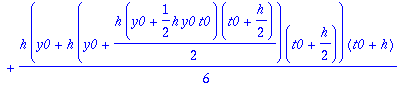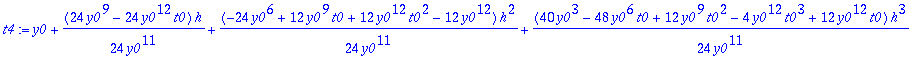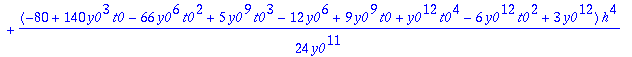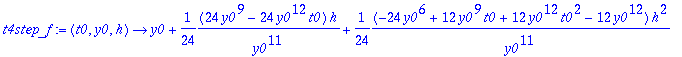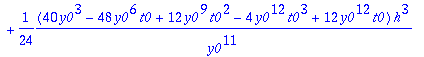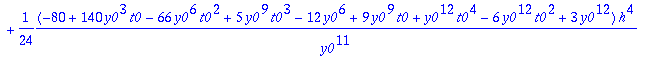4.
Warning, the name changecoords has been redefined
Taylorin menetelmä yhtälölle y'=f(t,y) tarkoittaa, että muodostetaan ratkaisufunktion y(t) derivaattoja pisteessä t ja käytetään niiden avulla laskettavaa, pisteessä t kehitettyä n:nnen asteen Taylorin polynomia ratkaisufunkton approksimoimiseen pisteessä t+h. Jos n=1, on kyseessä Eulerin menetelmä.
Koska y'(t)=f(t,y(t)), saadaan derivaatat muodostetuksi ketjusäännön avulla. Jos Maplelle annetaan määrittelemättömiä funktio(lausekke)ita
y(t) ym. sisältävä lauseke ja pyydetään derivoimaan, se soveltaa normaaleja derovoimissääntöjä (kuten ketjusääntöä).
Suoritetaan ensi ideointia.
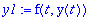
(t,y(t))+D[2](f)(t,y(t))*diff(y(t),t)](images/ratk460.gif)
| > |
y2:=subs(diff(y(t),t)=y1,%);
|
(t,y(t))+D[2](f)(t,y(t))*f(t,y(t))](images/ratk461.gif)
(t,y(t))+D[1,2](f)(t,y(t))*diff(y(t),t)+(D[1,2](f)(t,y(t))+D[2,2](f)(t,y(t))*diff(y(t),t))*f(t,y(t))+D[2](f)(t,y(t))*(D[1](f)(t,y(t))+D[2](f)(t,y(t))*diff(y(t),t))](images/ratk462.gif)
(t,y(t))+D[1,2](f)(t,y(t))*diff(y(t),t)+(D[1,2](f)(t,y(t))+D[2,2](f)(t,y(t))*diff(y(t),t))*f(t,y(t))+D[2](f)(t,y(t))*(D[1](f)(t,y(t))+D[2](f)(t,y(t))*diff(y(t),t))](images/ratk463.gif)
| > |
y3:=subs(diff(y(t),t)=y1,%);
|
(t,y(t))+D[1,2](f)(t,y(t))*f(t,y(t))+(D[1,2](f)(t,y(t))+D[2,2](f)(t,y(t))*f(t,y(t)))*f(t,y(t))+D[2](f)(t,y(t))*(D[1](f)(t,y(t))+D[2](f)(t,y(t))*f(t,y(t)))](images/ratk464.gif)
(t,y(t))+D[1,2](f)(t,y(t))*f(t,y(t))+(D[1,2](f)(t,y(t))+D[2,2](f)(t,y(t))*f(t,y(t)))*f(t,y(t))+D[2](f)(t,y(t))*(D[1](f)(t,y(t))+D[2](f)(t,y(t))*f(t,y(t)))](images/ratk465.gif)
Näin voidaan jatkaa. Yleisiä kaavoja ei kannata rakentaa pitkälle, vaan otetaan konkreettinen funktio.
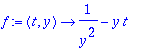
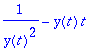
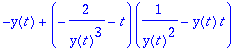
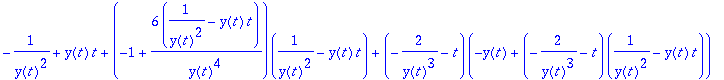
Näiden kokeilujen pohjalta johdutaan tehtäväpaperissa olevaan koodiin:
| > |
#read("c:\\usr\\heikki\\numsym04\\maple\\ns04.mpl");
|
| > |
#read("/home/apiola/opetus/numsym/04/maple/ns04.mpl");
|
| > |
read("/p/edu/mat-1.192/ns04.mpl");
|
![proc (f, t0, y0, h) local y1, y2, t, y, tay2; y1 := f(t,y(t)); y2 := diff(y1,t); y2 := subs(diff(y(t),t) = y1,y2); tay2 := y0+h*y1+1/2*h^2*y2; subs([t = t0, y(t) = y0],tay2) end proc](images/ratk470.gif)
![proc (f, t0, y0, h) local y1, y2, t, y, tay2; y1 := f(t,y(t)); y2 := diff(y1,t); y2 := subs(diff(y(t),t) = y1,y2); tay2 := y0+h*y1+1/2*h^2*y2; subs([t = t0, y(t) = y0],tay2) end proc](images/ratk471.gif)
![proc (f, t0, y0, h) local y1, y2, t, y, tay2; y1 := f(t,y(t)); y2 := diff(y1,t); y2 := subs(diff(y(t),t) = y1,y2); tay2 := y0+h*y1+1/2*h^2*y2; subs([t = t0, y(t) = y0],tay2) end proc](images/ratk472.gif)
![proc (f, t0, y0, h) local y1, y2, t, y, tay2; y1 := f(t,y(t)); y2 := diff(y1,t); y2 := subs(diff(y(t),t) = y1,y2); tay2 := y0+h*y1+1/2*h^2*y2; subs([t = t0, y(t) = y0],tay2) end proc](images/ratk473.gif)
Testataan, kuten tehtäväpaperissa:
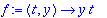
| > |
dsolve({diff(y(t),t)=t*y(t),y(0)=1},y(t));
|
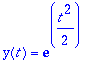
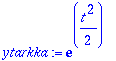
| > |
Y[0]:=1: h:=0.1: T:=seq(k*h,k=0..10);
for k to 11 do
Y[k]:=taystep2(f,T[k],Y[k-1],h):
end do:
|
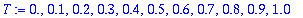
| > |
pisteet:=seq([T[k],Y[k-1]],k=1..11);
|
![pisteet := [0., 1], [.1, 1.005000000], [.2, 1.020125250], [.3, 1.045832406], [.4, 1.082907165], [.5, 1.132504314], [.6, 1.196207682], [.7, 1.276114355], [.8, 1.374949412], [.9, 1.496219950], [1.0, 1.64...](images/ratk478.gif)
![pisteet := [0., 1], [.1, 1.005000000], [.2, 1.020125250], [.3, 1.045832406], [.4, 1.082907165], [.5, 1.132504314], [.6, 1.196207682], [.7, 1.276114355], [.8, 1.374949412], [.9, 1.496219950], [1.0, 1.64...](images/ratk479.gif)
| > |
plot([[pisteet],ytarkka+0.01],t=0..1);
# Nostetaan tarkkaa hiukan, jotta erottuvat
|
![[Maple Plot]](images/ratk480.gif)
Nyt on helppoa jatkaa Taylorin 4:nnen asteen menetelmään:
Warning, the name changecoords has been redefined
| > |
#read("c:\\usr\\heikki\\numsym04\\maple\\ns04.mpl");
|
| > |
#read("/home/apiola/opetus/numsym/04/maple/ns04.mpl");
read("/p/edu/mat-1.192/ns04.mpl");
|
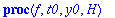
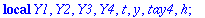
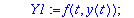

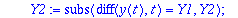

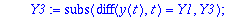

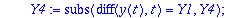
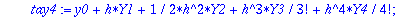
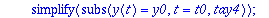
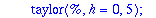
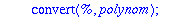
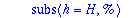

Kaksi viimeistä riviä edustavat "laiskan Maple-miehen" tapaa kerätä kunkin h:n potenssin kertoimet. (Varmaan löytyy suorempiakin.). Tässä täytyy vielä konvertoida tulos polynomiksi, sillä
taylor
palauttaa "sarja-tietorakenteen", jossa on jäännöstermi mukana.
(Kts. ?taylor)
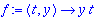
Kiintoisaa on verrata tay4step:iä ja rk4step:iä
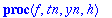
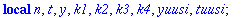
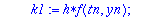
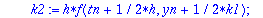
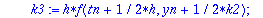
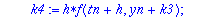
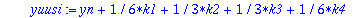

| > |
rk:=rk4step(f,t0,y0,h):
|
| > |
t4:=tay4step(f,t0,y0,'h'):
|
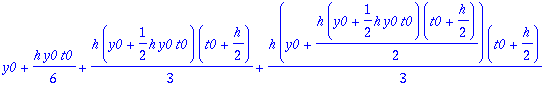
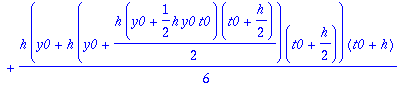
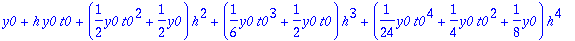
Tässä tapauksessa taylorin menetelmä antaa jopa yksinkertaisemman lausekkeen.
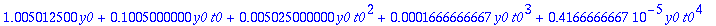
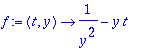
| > |
t4:=tay4step(f,t0,y0,h);
|
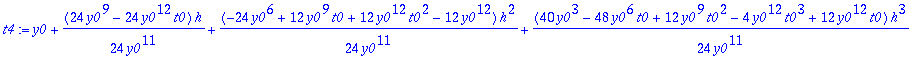
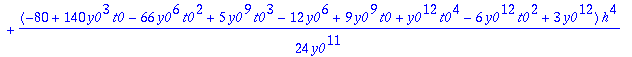
| > |
t4step_f:=unapply(t4,t0,y0,h);
|
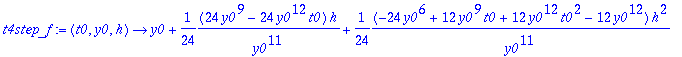
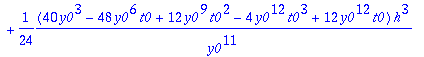
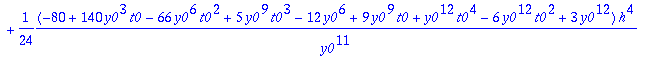
Meillä on nyt funktio
t4step_f
, joka suorittaa Taylorin 4:nnen asteen menetelmän askeleen juuri tähän konkreettiseen funktioon f liittyen. Huomataan, että
unapplyn
käyttö on olennaista. Tässä vaiheessa voidaan
tehdä haluttuja sievennysoperaatioita.
Kirjoitetaan nyt funktio, joka laskee n askelta käyttäen tätä askelfunktiota. Nyt siis funktio f ei enää ole argumenttilistalla, vaan sen vaikutus tulee mukaan kutsuttaessa
t4step_f
-funktiota.
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4115.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4116.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4117.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4118.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4119.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4120.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4121.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4122.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4123.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4124.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4125.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4126.gif)
![proc (vali, y0, n) local a, b, k, h, t, y; a := vali[1]; b := vali[2]; h := (b-a)/n; a := evalf(a); b := evalf(b); h := evalf(h); t[0] := a; y[0] := y0; for k from 0 to n-1 do y[k+1] := t4step_f(t[k],y...](images/ratk4127.gif)
Kutsuparametreina ovat
vali
,
alkuarvo
välin alkupisteessä ja askelten lukumäärä. (Huomaa, että
vali j
a
y0
ovat aivan samoin kuin Matlabin ODE-funktioissa. Askeleen suorittava
t4step_f
on "kolvattu" kiinteän nimisenä koodiin.
| > |
T4pisteet:=tay4_f([1,2],1,10);
|
![T4pisteet := [[1., 1], [1.100000000, .9954750000], [1.200000000, .9836463965], [1.300000000, .9667976911], [1.400000000, .9468193314], [1.500000000, .9252337022], [1.600000000, .9032115004], [1.7000000...](images/ratk4128.gif)
![T4pisteet := [[1., 1], [1.100000000, .9954750000], [1.200000000, .9836463965], [1.300000000, .9667976911], [1.400000000, .9468193314], [1.500000000, .9252337022], [1.600000000, .9032115004], [1.7000000...](images/ratk4129.gif)
![T4pisteet := [[1., 1], [1.100000000, .9954750000], [1.200000000, .9836463965], [1.300000000, .9667976911], [1.400000000, .9468193314], [1.500000000, .9252337022], [1.600000000, .9032115004], [1.7000000...](images/ratk4130.gif)
Siistiä!
Verrataan RK4-pisteisiin:
![[[1, 1], [1.100000000, .9954745362], [1.200000000, .9836448154], [1.300000000, .9667952785], [1.400000000, .9468167382], [1.500000000, .9252316601], [1.600000000, .9032106430], [1.700000000, .881596397...](images/ratk4131.gif)
![[[1, 1], [1.100000000, .9954745362], [1.200000000, .9836448154], [1.300000000, .9667952785], [1.400000000, .9468167382], [1.500000000, .9252316601], [1.600000000, .9032106430], [1.700000000, .881596397...](images/ratk4132.gif)
![[[1, 1], [1.100000000, .9954745362], [1.200000000, .9836448154], [1.300000000, .9667952785], [1.400000000, .9468167382], [1.500000000, .9252316601], [1.600000000, .9032106430], [1.700000000, .881596397...](images/ratk4133.gif)
| > |
T4pisteet[-1][-1]; # Viimeisen parin viimeinen alkio, eli y(2):n approksimaatio
|
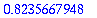
| > |
RK4(f,[1,2],1,10)[-1][-1];
|
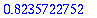
| > |
tay4_f([1,2],1,10)[-1][-1]; # Yllä oleva yhdellä rivillä.
|
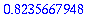
5:n numeron tarkkuudella samat (6:nnessa yhden numeron ero). Kumpi on tarkempi?
Nyt päästään tutkimaan tehtävän tilannetta
Katsotaan tehtävässä kysyttyja askelpituuksia.
| > |
Digits:=10: # Oletusarvo
|
| > |
tayarvot:=seq(tay4_f([1,2],1,2^k)[-1][-1],k=2..10);
|
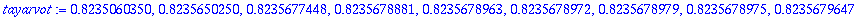
| > |
RKarvot:=seq(RK4(f,[1,2],1,2^k)[-1][-1],k=2..10);
|
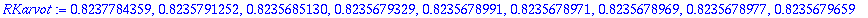
Mikä on tarkin arvo? Turha toivoa, että kahta viimeistä numeroa voisi saada oikein. Askelpituuden puolittaminen ei loputtomasti lisää tarkkuutta, vaan jostain alkaen tulokset alkavat huonontua.
Otetaan viimeistä edellisten keskiarvo:
| > |
tarkinkai:=.8235678976;
|
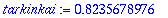
| > |
tayvirheet:=seq((tarkinkai-tayarvot[k]),k=1..nops([tayarvot])-1);
|
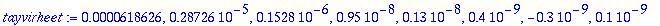
| > |
RKvirheet:=seq((tarkinkai-RKarvot[k]),k=1..nops([tayarvot])-1);
|

| > |
seq(tayvirheet[i+1]/tayvirheet[i],i=1..nops([tayarvot])-2);
|
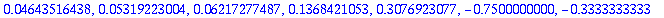
| > |
seq(RKvirheet[i+1]/RKvirheet[i],i=1..nops([tayarvot])-2);
|
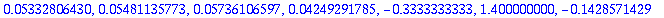
| > |
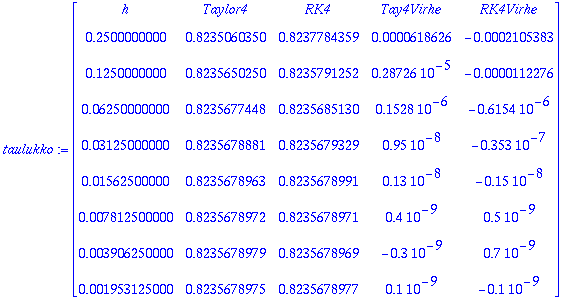
taulukko:=<<h,seq(2.^(-k),k=2..9)>|<Taylor4,tayarvot[1..-2]>|<RK4,RKarvot[1..-2]>|<Tay4Virhe,tayvirheet>|<RK4Virhe,RKvirheet>>;
|
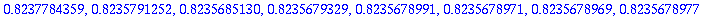
| > |
tayarvot20:=seq(tay4_f([1,2],1,2^k)[-1][-1],k=2..10);
|
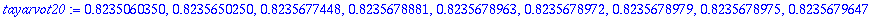
| > |
RKarvot20:=seq(RK4(f,[1,2],1,2^k)[-1][-1],k=2..10);
|
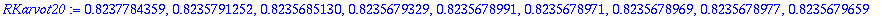
| > |
melkeintarkka:=tayarvot20[-1];
|
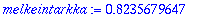
| > |
tayvirheet:=seq((melkeintarkka-tayarvot[k]),k=1..nops([tayarvot20]));
|
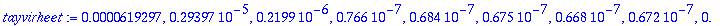
| > |
RKvirheet:=seq((melkeintarkka-RKarvot[k]),k=1..nops([tayarvot]));
|
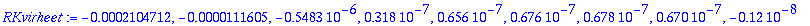
| > |
seq(tayvirheet[i+1]/tayvirheet[i],i=1..nops([tayarvot20])-1);
|
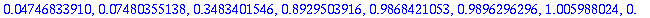
| > |
seq(RKvirheet[i+1]/RKvirheet[i],i=1..nops([tayarvot])-1);
|
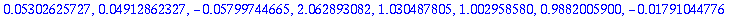
| > |
taulukko:=<<h,seq(2.^(-k),k=2..10)>|<Taylor4,tayarvot>|<RK4,RKarvot>|<Tay4Virhe,tayvirheet>|<RK4Virhe,RKvirheet>>;
|

Kysymys: Kuinka monta oikeaa numeroa?
Kun taulukoa katsoo, niin h=2^(-5) on pienin askel, jolla virhe pienenee normaalin näköisesti. Siitä alaspäin tulokset jopa huononevat.
Lisätään ensin laskentatarkkuutta.
| > |
tarkinkai; # Ainakin 2 viimeistä numeroa ovat "satunnaislukuja".
|

Sama tarkemmin.
| > |
tayarvot20:=seq(tay4_f([1,2],1,2^k)[-1][-1],k=2..10);
|

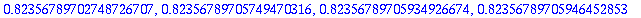
| > |
RKarvot20:=seq(RK4(f,[1,2],1,2^k)[-1][-1],k=2..10);
|

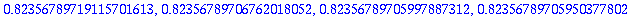
| > |
tarkinkai20:=tayarvot20[-1];
|
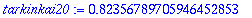
| > |
tayvirheet20:=seq((tarkinkai20-tayarvot[k]),k=1..nops([tayarvot20]));
|
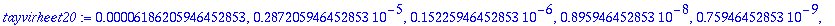
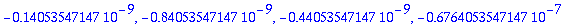
| > |
RKvirheet20:=seq((tarkinkai20-RKarvot[k]),k=1..nops([tayarvot20]));
|
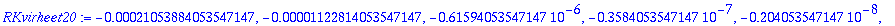
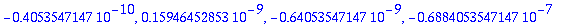

Globaalin virheen tulisi pienetyä suunnilleen tällä kertoimella, kun askel puolittuu.
| > |
seq(tayvirheet20[i+1]/tayvirheet20[i],i=1..nops([tayarvot20])-1);
|
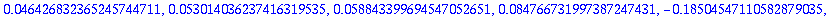
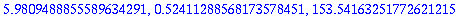
| > |
seq(RKvirheet20[i+1]/RKvirheet20[i],i=1..nops([tayarvot20])-1);
|
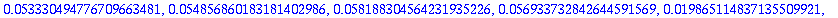
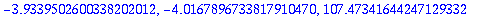
Virhekäytös on järkevännäköistä arvoon i=5 saakka, eli h=1/2^6 = 1/64.
| > |
tayarvot20[5],RKarvot20[5];
|
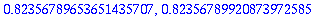
Kertalukua lisää, yleinen Taystep
Warning, the name changecoords has been redefined
| > |
#read("c:\\usr\\heikki\\numsym04\\maple\\ns04.mpl");
|
| > |
#read("/home/apiola/opetus/numsym/04/maple/ns04.mpl");
read("/p/edu/mat-1.192/ns04.mpl");
|
![proc (f, N) local Y, k, t, y, tay, t0, y0, h; Y := array(1 .. N); Y[1] := f(t,y(t)); for k from 2 to N do Y[k] := diff(Y[k-1],t); Y[k] := subs(diff(y(t),t) = Y[1],Y[k]) end do; k := 'k'; tay := y0+sum(...](images/ratk4170.gif)
![proc (f, N) local Y, k, t, y, tay, t0, y0, h; Y := array(1 .. N); Y[1] := f(t,y(t)); for k from 2 to N do Y[k] := diff(Y[k-1],t); Y[k] := subs(diff(y(t),t) = Y[1],Y[k]) end do; k := 'k'; tay := y0+sum(...](images/ratk4171.gif)
![proc (f, N) local Y, k, t, y, tay, t0, y0, h; Y := array(1 .. N); Y[1] := f(t,y(t)); for k from 2 to N do Y[k] := diff(Y[k-1],t); Y[k] := subs(diff(y(t),t) = Y[1],Y[k]) end do; k := 'k'; tay := y0+sum(...](images/ratk4172.gif)
![proc (f, N) local Y, k, t, y, tay, t0, y0, h; Y := array(1 .. N); Y[1] := f(t,y(t)); for k from 2 to N do Y[k] := diff(Y[k-1],t); Y[k] := subs(diff(y(t),t) = Y[1],Y[k]) end do; k := 'k'; tay := y0+sum(...](images/ratk4173.gif)
![proc (f, N) local Y, k, t, y, tay, t0, y0, h; Y := array(1 .. N); Y[1] := f(t,y(t)); for k from 2 to N do Y[k] := diff(Y[k-1],t); Y[k] := subs(diff(y(t),t) = Y[1],Y[k]) end do; k := 'k'; tay := y0+sum(...](images/ratk4174.gif)
![proc (f, N) local Y, k, t, y, tay, t0, y0, h; Y := array(1 .. N); Y[1] := f(t,y(t)); for k from 2 to N do Y[k] := diff(Y[k-1],t); Y[k] := subs(diff(y(t),t) = Y[1],Y[k]) end do; k := 'k'; tay := y0+sum(...](images/ratk4175.gif)
![proc (f, N) local Y, k, t, y, tay, t0, y0, h; Y := array(1 .. N); Y[1] := f(t,y(t)); for k from 2 to N do Y[k] := diff(Y[k-1],t); Y[k] := subs(diff(y(t),t) = Y[1],Y[k]) end do; k := 'k'; tay := y0+sum(...](images/ratk4176.gif)
![proc (f, N) local Y, k, t, y, tay, t0, y0, h; Y := array(1 .. N); Y[1] := f(t,y(t)); for k from 2 to N do Y[k] := diff(Y[k-1],t); Y[k] := subs(diff(y(t),t) = Y[1],Y[k]) end do; k := 'k'; tay := y0+sum(...](images/ratk4177.gif)
![proc (f, N) local Y, k, t, y, tay, t0, y0, h; Y := array(1 .. N); Y[1] := f(t,y(t)); for k from 2 to N do Y[k] := diff(Y[k-1],t); Y[k] := subs(diff(y(t),t) = Y[1],Y[k]) end do; k := 'k'; tay := y0+sum(...](images/ratk4178.gif)
![proc (f, N) local Y, k, t, y, tay, t0, y0, h; Y := array(1 .. N); Y[1] := f(t,y(t)); for k from 2 to N do Y[k] := diff(Y[k-1],t); Y[k] := subs(diff(y(t),t) = Y[1],Y[k]) end do; k := 'k'; tay := y0+sum(...](images/ratk4179.gif)
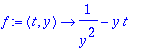
| > |
MainTaylor(4,f,[1,2],1,10);
|
![[[1., 1], [1.100000000, .9954750000], [1.200000000, .9836463963], [1.300000000, .9667976913], [1.400000000, .9468193317], [1.500000000, .9252337025], [1.600000000, .9032115004], [1.700000000, .88159565...](images/ratk4181.gif)
![[[1., 1], [1.100000000, .9954750000], [1.200000000, .9836463963], [1.300000000, .9667976913], [1.400000000, .9468193317], [1.500000000, .9252337025], [1.600000000, .9032115004], [1.700000000, .88159565...](images/ratk4182.gif)
![[[1., 1], [1.100000000, .9954750000], [1.200000000, .9836463963], [1.300000000, .9667976913], [1.400000000, .9468193317], [1.500000000, .9252337025], [1.600000000, .9032115004], [1.700000000, .88159565...](images/ratk4183.gif)
| > |
MainTaylor(5,f,[1,2],1,10);
|
![[[1., 1], [1.100000000, .9954770000], [1.200000000, .9836486133], [1.300000000, .9667995333], [1.400000000, .9468207250], [1.500000000, .9252347875], [1.600000000, .9032124675], [1.700000000, .88159664...](images/ratk4184.gif)
![[[1., 1], [1.100000000, .9954770000], [1.200000000, .9836486133], [1.300000000, .9667995333], [1.400000000, .9468207250], [1.500000000, .9252347875], [1.600000000, .9032124675], [1.700000000, .88159664...](images/ratk4185.gif)
![[[1., 1], [1.100000000, .9954770000], [1.200000000, .9836486133], [1.300000000, .9667995333], [1.400000000, .9468207250], [1.500000000, .9252347875], [1.600000000, .9032124675], [1.700000000, .88159664...](images/ratk4186.gif)
| > |
MainTaylor(6,f,[1,2],1,10);
|
![[[1., 1], [1.100000000, .9954766917], [1.200000000, .9836482613], [1.300000000, .9667992349], [1.400000000, .9468205103], [1.500000000, .9252346550], [1.600000000, .9032124008], [1.700000000, .88159662...](images/ratk4187.gif)
![[[1., 1], [1.100000000, .9954766917], [1.200000000, .9836482613], [1.300000000, .9667992349], [1.400000000, .9468205103], [1.500000000, .9252346550], [1.600000000, .9032124008], [1.700000000, .88159662...](images/ratk4188.gif)
![[[1., 1], [1.100000000, .9954766917], [1.200000000, .9836482613], [1.300000000, .9667992349], [1.400000000, .9468205103], [1.500000000, .9252346550], [1.600000000, .9032124008], [1.700000000, .88159662...](images/ratk4189.gif)
| > |
MainTaylor(6,f,[1,2],1,20);
|
![[[1., 1], [1.050000000, .9988109951], [1.100000000, .9954767260], [1.150000000, .9903231775], [1.200000000, .9836483007], [1.250000000, .9757243506], [1.300000000, .9667992701], [1.350000000, .95709750...](images/ratk4190.gif)
![[[1., 1], [1.050000000, .9988109951], [1.100000000, .9954767260], [1.150000000, .9903231775], [1.200000000, .9836483007], [1.250000000, .9757243506], [1.300000000, .9667992701], [1.350000000, .95709750...](images/ratk4191.gif)
![[[1., 1], [1.050000000, .9988109951], [1.100000000, .9954767260], [1.150000000, .9903231775], [1.200000000, .9836483007], [1.250000000, .9757243506], [1.300000000, .9667992701], [1.350000000, .95709750...](images/ratk4192.gif)
![[[1., 1], [1.050000000, .9988109951], [1.100000000, .9954767260], [1.150000000, .9903231775], [1.200000000, .9836483007], [1.250000000, .9757243506], [1.300000000, .9667992701], [1.350000000, .95709750...](images/ratk4193.gif)
![[[1., 1], [1.050000000, .9988109951], [1.100000000, .9954767260], [1.150000000, .9903231775], [1.200000000, .9836483007], [1.250000000, .9757243506], [1.300000000, .9667992701], [1.350000000, .95709750...](images/ratk4194.gif)
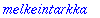
| > |
MainTaylor(7,f,[1,2],1,10);
|
![[[1., 1], [1.100000000, .9954767305], [1.200000000, .9836483057], [1.300000000, .9667992746], [1.400000000, .9468205422], [1.500000000, .9252346786], [1.600000000, .9032124167], [1.700000000, .88159663...](images/ratk4196.gif)
![[[1., 1], [1.100000000, .9954767305], [1.200000000, .9836483057], [1.300000000, .9667992746], [1.400000000, .9468205422], [1.500000000, .9252346786], [1.600000000, .9032124167], [1.700000000, .88159663...](images/ratk4197.gif)
![[[1., 1], [1.100000000, .9954767305], [1.200000000, .9836483057], [1.300000000, .9667992746], [1.400000000, .9468205422], [1.500000000, .9252346786], [1.600000000, .9032124167], [1.700000000, .88159663...](images/ratk4198.gif)
Kertalukua 7 olevalla Taylorilla päästään jo 10:llä askeleella tarkkaan (10 numeroa) tulokseen.
Analyyttinen ratkaisu on tolkuton, "numeric" voi aiheuttaa työarkin korruptoitumista.
| > |
#nratk:=dsolve({diff(y(t),t)=f(t,y(t)),y(1)=1},y(t),numeric);
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[t[n]+h, 1/3*t[n]^3+1/9*h*(2*t[n]^2+3*(t[n]+1/2*h)^2+4*(t[n]+3/4*h)^2), 1/72*h*(-5*t[n]^2+6*(t[n]+1/2*h)^2+8*(t[n]+3/4*h)^2-9*(t[n]+h)^2)]](images/ratk429.gif)
![Y[n+1] := 1/3*t[n]^3+1/9*h*(2*t[n]^2+3*(t[n]+1/2*h)^2+4*(t[n]+3/4*h)^2)](images/ratk430.gif)
![1/3*t[n]^3+1/9*(t[n+1]-t[n])*(2*t[n]^2+3*(1/2*t[n]+1/2*t[n+1])^2+4*(1/4*t[n]+3/4*t[n+1])^2)](images/ratk431.gif)
![]()
![]()
![]()
![]()
![]()
![[t[n]+h, 1/4*t[n]^4+1/9*h*(2*t[n]^3+3*(t[n]+1/2*h)^3+4*(t[n]+3/4*h)^3), 1/72*h*(-5*t[n]^3+6*(t[n]+1/2*h)^3+8*(t[n]+3/4*h)^3-9*(t[n]+h)^3)]](images/ratk437.gif)
![Y[n+1] := 1/4*t[n]^4+1/9*h*(2*t[n]^3+3*(t[n]+1/2*h)^3+4*(t[n]+3/4*h)^3)](images/ratk438.gif)
![virhearvio := 1/72*h*(-5*t[n]^3+6*(t[n]+1/2*h)^3+8*(t[n]+3/4*h)^3-9*(t[n]+h)^3)](images/ratk439.gif)
![]()
![]()
![LKV[n+1] := h*t[n]^3+3/2*t[n]^2*h^2+t[n]*h^3+1/4*h^4-1/9*h*(2*t[n]^3+3*(t[n]+1/2*h)^3+4*(t[n]+3/4*h)^3)](images/ratk442.gif)
![]()
![]()
![]()
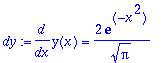
![[Maple Plot]](images/ratk457.gif)
![matrix([[0., 0., 0.], [.2, .222702806851365176, .2227025892], [.4, .428392530623065315, .4283923550], [.6, .603856241704604391, .6038560908], [.8, .742101083482852975, .7421009647], [1.0, .842698530175...](images/ratk458.gif)
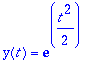
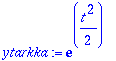
![[Maple Plot]](images/ratk480.gif)