ratk7.nb

•Tehtävä 1

In[1]:=

Out[1]=

${{z -> -1}, {z -> (-1)^(1/7)}, {z -> -(-1)^(2/7)}, {z -> (-1)^(3/7)}, {z -> -(-1)^(4/7)}, {z -> (-1)^(5/7)}, {z -> -(-1)^(6/7)}}$

In[2]:=

Out[2]=

{-1, Cos[π/7] + i Sin[π/7], -Cos[(2 π)/7] - i Sin[(2 π)/7], Cos[(3 π) ... [(4 π)/7], Cos[(5 π)/7] + i Sin[(5 π)/7], -Cos[(6 π)/7] - i Sin[(6 π)/7]}

In[3]:=

Out[3]=

Juurten etäisyys origosta voidaan nähdä suoraan kohdista ratk ja summamuoto. Kaikki juuret ovat siis etäisyydellä 1 origosta. Kompleksilukujen itseisarvo eli etäisyys origosta saadaan myös komennolla Abs.

In[4]:=

Out[4]=

In[5]:=

Out[5]=

Juurten napakulmat nähdään suoraan kohdasta summamuoto. Ne voidaan myös laskea komennolla Arg.

In[6]:=

Out[6]=

Seuraavassa on vielä piirretty juuret kompleksitasoon. Ensin on muodostettu juuria vastaavat kompleksitason pisteet ja sitten ne on piirretty ListPlot-komennolla, jossa on optioksi annettu pisteen koko.

In[7]:=

Out[7]=

{{-1, 0}, {Cos[π/7], Sin[π/7]}, {-Cos[(2 π)/7], -Sin[(2 π)/7]}, {Cos[(3 &# ... [(4 π)/7]}, {Cos[(5 π)/7], Sin[(5 π)/7]}, {-Cos[(6 π)/7], -Sin[(6 π)/7]}}

In[8]:=

[Graphics:HTMLFiles/ratk7_16.gif]

Out[8]=

Ratkaisut sijaitsevat tasavälisesti ympyrän kehällä.

•Tehtävä 2

In[9]:=

Out[9]=

${{z -> -2 + i}, {z -> 1 - i 3^(1/2)}, {z -> 1 + i 3^(1/2)}}$

In[10]:=

Out[10]=

${-2 + i, 1 - i 3^(1/2), 1 + i 3^(1/2)}$

•Tehtävä 3

In[11]:=

Out[11]=

In[12]:=

Out[12]=

In[13]:=

Out[13]=

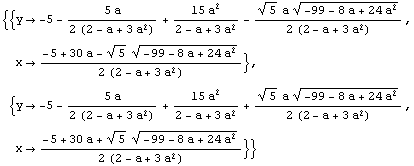
${{y -> -5 - (5 a)/(2 (2 - a + 3 a^2)) + (15 a^2)/(2 - a + 3 a^2) - (5^(1/2) a (-99 - 8 a + ... 2 (2 - a + 3 a^2)), x -> (-5 + 30 a + 5^(1/2) (-99 - 8 a + 24 a^2)^(1/2))/(2 (2 - a + 3 a^2))}}$

Yhtälöparilla on reaalisia ratkaisuja, kun juurrettava . Lisäksi nimittäjässä oleva ei saa olla nolla.

In[14]:=

In[15]:=

Out[15]=

In[16]:=

Out[16]=

${{a -> 1/6 (1 - i 23^(1/2))}, {a -> 1/6 (1 + i 23^(1/2))}}$

Ratkaisussa oleva nimittäjä ei siis ole nolla millään reaaliluvulla a. Siten ainoa ehto sille, että ratkaisut ovat reaalisia, on tai .

•Tehtävä 4

In[17]:=

Out[17]=

In[18]:=

Out[18]=

Lasketaan ympyröiden leikkauspisteet ja sijoitetaan ne muuttujiin lp1 ja lp2.

In[19]:=

Out[19]=

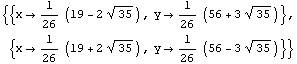
${{x -> 1/26 (19 - 2 35^(1/2)), y -> 1/26 (56 + 3 35^(1/2))}, {x -> 1/26 (19 + 2 35^(1/2)), y -> 1/26 (56 - 3 35^(1/2))}}$

In[20]:=

Out[20]=

${{1/26 (19 - 2 35^(1/2)), 1/26 (56 + 3 35^(1/2))}, {1/26 (19 + 2 35^(1/2)), 1/26 (56 - 3 35^(1/2))}}$

Leikkauspisteiden etäisyydet origosta ovat etaisyys1 ja etaisyys2.

In[21]:=

Out[21]=

In[22]:=

Out[22]=

In[23]:=

Out[23]=

In[24]:=

Out[24]=

Leikkauspisteiden välinen vektori on lp1lp2 ja leikkauspisteiden välinen etäisyys valinenetaisyys.

In[25]:=

Out[25]=

${(2 35^(1/2))/13, -(3 35^(1/2))/13}$

In[26]:=

Out[26]=

In[27]:=

Out[27]=

Seuraavassa on vielä piirretty ympyrät ImplicitPlot-komennolla.

In[28]:=

In[29]:=

[Graphics:HTMLFiles/ratk7_61.gif]

Out[29]=

In[30]:=

Out[30]=

In[31]:=

Out[31]=

•Tehtävä 5

Funktio pkert muodostaa vektorin, jossa on painokertoimet, kun osavälejä on n kpl.

In[32]:=

$pkert[n_] := Flatten[{1, Table[2, {i, 1, n - 1}], 1}]$

In[33]:=

Funktio fktarvot laskee funktion f arvot välillä 0...1, kun osavälejä on n kpl.

In[34]:=

$fktarvot[n_] := Table[f[x], {x, 0, 1, 1/n}]$

Funktio kerroin on puolisuunnikassäännössä oleva kerroin . Tässä tehtävässä ja .

In[35]:=

Funktio puolisuunnikasmenet laskee funktion f määrätyn integraalin välillä 0...1 käyttäen n osaväliä.

In[36]:=

Esimerkiksi neljällä osavälillä saadaan määrätylle integraalille arvio:

In[37]:=

Out[37]=

Vastaavalla tavalla saadaan arviot myös muille n:n arvoille. Nämä voidaan laskea myös yhdellä komennolla:

In[38]:=

Out[38]=

Verrataan saatuja arvoja vielä NIntegrate-komennolla saatuun arvoon.

In[39]:=

Out[39]=

In[40]:=

Out[40]=

•Tehtävä 6

In[41]:=

Out[41]=

In[42]:=

Out[42]=

a) Helsingin ja Tokion välinen etäisyys

In[43]:=

Out[43]=

In[44]:=

Out[44]=

In[45]:=

$General :: spell1 : Possible spelling error: new symbol name \" levT \" is similar to existing symbol \" levH \".$

Out[45]=

In[46]:=

$General :: spell1 : Possible spelling error: new symbol name \" pitT \" is similar to existing symbol \" pitH \".$

Out[46]=

In[47]:=

Out[47]=

b) Reykjavikin ja Sydneyn välinen etäisyys

In[48]:=

$General :: spell : Possible spelling error: new symbol name \" levR \" is similar to existing symbols {levH, levT} .$

Out[48]=

In[49]:=

$General :: spell : Possible spelling error: new symbol name \" pitR \" is similar to existing symbols {pitH, pitT} .$

Out[49]=

In[50]:=

$General :: spell : Possible spelling error: new symbol name \" levS \" is similar to existing symbols {levH, levR, levT} .$

Out[50]=

In[51]:=

$General :: spell : Possible spelling error: new symbol name \" pitS \" is similar to existing symbols {pitH, pitR, pitT} .$

Out[51]=

In[52]:=

Out[52]=

Alapuolella tehtävä on ratkaistu myös muodostamalla funktio, johon sopivat maantieteelliset koordinaatit sijoitetaan.

In[53]:=

In[54]:=

Out[54]=

In[55]:=

Out[55]=

•Tehtävä 7

In[56]:=

Out[56]=

In[57]:=

In[58]:=

Out[58]=

In[59]:=

[Graphics:HTMLFiles/ratk7_124.gif]

Out[59]=

In[60]:=

Out[60]=

In[61]:=

[Graphics:HTMLFiles/ratk7_129.gif]

Out[61]=

Kun torusta leikataan tasoilla , ovat leikkauskäyrät sisäkkäisiä origokeskisiä ympyröitä. Kun , niin leikkauskäyränä on 2-säteinen origokeskinen ympyrä. (Sitä Mathematica ei kuitenkaan suostunut piirtämään.)

In[62]:=

Out[62]=

In[63]:=

[Graphics:HTMLFiles/ratk7_136.gif]

Out[63]=

In[64]:=

Out[64]=

In[65]:=

[Graphics:HTMLFiles/ratk7_141.gif]

Out[65]=

In[66]:=

Out[66]=

In[67]:=

[Graphics:HTMLFiles/ratk7_146.gif]

Out[67]=

In[68]:=

Out[68]=

In[69]:=

[Graphics:HTMLFiles/ratk7_151.gif]

Out[69]=

In[70]:=

Out[70]=

In[71]:=

[Graphics:HTMLFiles/ratk7_156.gif]

Out[71]=

In[72]:=

Out[72]=

In[73]:=

[Graphics:HTMLFiles/ratk7_161.gif]

Out[73]=

Kun torusta leikataan tasoilla , missä , niin syntyy kuudenlaisia leikkauskuvioita. Kun , syntyy kaksi erillistä ympyrää. Kun , syntyy leikkaus4-tyyppisiä kuvioita. Kun , syntyy kuvio leikkaus5. Kun , syntyy leikkaus6-tyyppinen kuvio. Kun syntyy leikkaus7-tyyppinen kuvio. Kun syntyy leikkaus8-tyyppisiä kuvioita. Kun , syntyy pelkkä piste.

•Tehtävä 8

In[74]:=

Out[74]=

Seuraavat tulostukset ovat hieman pitkiä; tämän johdosta puolipisteet syötteiden perään.

In[75]:=

In[76]:=

Out[76]=

In[77]:=

In[78]:=

Out[78]=

In[79]:=

Out[79]=

Vakion a pitää siis olla .

•Tehtävä 9

Kyseessä on siis geometrinen sarja, joka suppenee, kun .

In[80]:=

Out[80]=

Määritellään summafunktio ja piirretään sen kuvaaja.

In[81]:=

$summa[x_ /; x < -2 || x > 0] = Sum[((2 * x - 1)/(3 * x + 1))^k, {k, 0, Infinity}]$

Out[81]=

In[82]:=

$General :: stop : Further output of Plot :: \" plnr \" will be suppressed during this calculation.$

[Graphics:HTMLFiles/ratk7_193.gif]

Out[82]=

•Tehtävä 10

Toisen asteen yhtälön ratkaisukaava:

In[83]:=

Out[83]=

${{x -> (-b - (b^2 - 4 a c)^(1/2))/(2 a)}, {x -> (-b + (b^2 - 4 a c)^(1/2))/(2 a)}}$

In[84]:=

Out[84]=

${{x -> -1/15 i (-i + 179^(1/2))}, {x -> 1/15 i (i + 179^(1/2))}}$

In[85]:=

Out[85]=

${{x -> -1/15 i (-i + 179^(1/2))}, {x -> 1/15 i (i + 179^(1/2))}}$

Molemmilla tavoilla saadaan samat ratkaisut.

Kolmannen asteen yhtälön ratkaisukaava:

In[86]:=

In[87]:=

Out[87]=

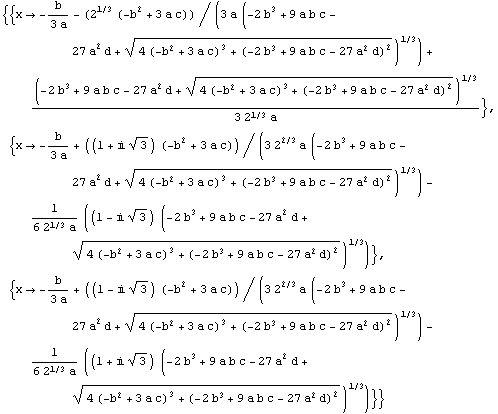
${{x -> -b/(3 a) - (2^(1/3) (-b^2 + 3 a c))/(3 a (-2 b^3 + 9 a b c - 27 a^2 d + (4 (-b^2 + 3 ... b^3 + 9 a b c - 27 a^2 d + (4 (-b^2 + 3 a c)^3 + (-2 b^3 + 9 a b c - 27 a^2 d)^2)^(1/2))^(1/3))}}$

In[88]:=

Out[88]=

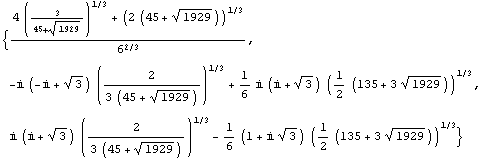
${(4 (3/(45 + 1929^(1/2)))^(1/3) + (2 (45 + 1929^(1/2)))^(1/3))/6^(2/3), -i (-i + 3^(1/2)) (2/( ... + 3^(1/2)) (2/(3 (45 + 1929^(1/2))))^(1/3) - 1/6 (1 + i 3^(1/2)) (1/2 (135 + 3 1929^(1/2)))^(1/3)}$

In[89]:=

Out[89]=

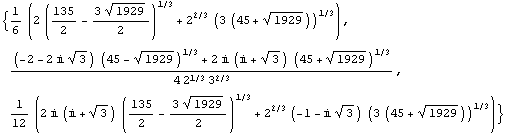
${1/6 (2 (135/2 - (3 1929^(1/2))/2)^(1/3) + 2^(2/3) (3 (45 + 1929^(1/2)))^(1/3)), ((-2 - 2 i 3^ ... 3^(1/2)) (135/2 - (3 1929^(1/2))/2)^(1/3) + 2^(2/3) (-1 - i 3^(1/2)) (3 (45 + 1929^(1/2)))^(1/3))}$

In[90]:=

Out[90]=

Molemmilla tavoilla saadaan samat ratkaisut.

Converted by Mathematica (August 25, 2003)