•Tehtävä 1

In[1]:=

summat = Table[ Sum[k^2, {k, 1, n}], {n, 1, 10}]

Out[1]=

{1, 5, 14, 30, 55, 91, 140, 204, 285, 385}

In[2]:=

tekijat = FactorInteger[summat]

Out[2]=

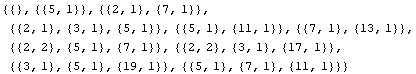
{{}, {{5, 1}}, {{2, 1}, {7, 1}}, {{2, 1}, {3, 1}, {5, 1}}, {{5, 1}, {11, 1}}, {{7, 1}, {13, 1} ... {5, 1}, {7, 1}}, {{2, 2}, {3, 1}, {17, 1}}, {{3, 1}, {5, 1}, {19, 1}}, {{5, 1}, {7, 1}, {11, 1}}}

Kunkin summan alkutekijät (tekijä ja montako kertaa se esiintyy):

In[3]:=

ColumnForm[tekijat]

Out[3]=
{}
{{5, 1}}
{{2, 1}, {7, 1}}
{{2, 1}, {3, 1}, {5, 1}}
{{5, 1}, {11, 1}}
{{7, 1}, {13, 1}}
{{2, 2}, {5, 1}, {7, 1}}
{{2, 2}, {3, 1}, {17, 1}}
{{3, 1}, {5, 1}, {19, 1}}
{{5, 1}, {7, 1}, {11, 1}}

In[4]:=

PrimeQ[summat]

Out[4]=

{False, True, False, False, False, False, False, False, False, False}

•Tehtävä 2

Lista lukuja välillä 0-90 astetta:

In[5]:=

kulma = Range[ 0, 90 ]

Out[5]=

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, ... 6, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90}

Lasketaan vastaavat sinin arvot:

In[6]:=

sini = Sin[ kulma Degree] // N

Out[6]=

{0.`, 0.01745240643728351`, 0.03489949670250097`, 0.052335956242943835`, 0.0697564737441253`, ... 0917455`, 0.9975640502598242`, 0.9986295347545738`, 0.9993908270190958`, 0.9998476951563913`, 1.`}

Lasketaan vastaavat kosinin arvot:

In[7]:=

kosini = Cos[kulma Degree] // N

Out[7]=

{1.`, 0.9998476951563913`, 0.9993908270190958`, 0.9986295347545738`, 0.9975640502598242`, 0.99 ... 814`, 0.06975647374412523`, 0.052335956242943966`, 0.03489949670250108`, 0.0174524064372836`, 0.`}

Taulukko:

In[8]:=

Transpose[{kulma, sini, kosini}] // TableForm

Out[8]//TableForm=
0 0.` 1.`
1 0.01745240643728351` 0.9998476951563913`
2 0.03489949670250097` 0.9993908270190958`
3 0.052335956242943835` 0.9986295347545738`
4 0.0697564737441253` 0.9975640502598242`
5 0.08715574274765817` 0.9961946980917455`
6 0.10452846326765347` 0.9945218953682733`
7 0.12186934340514748` 0.992546151641322`
8 0.13917310096006544` 0.9902680687415704`
9 0.15643446504023087` 0.9876883405951378`
10 0.17364817766693033` 0.984807753012208`
11 0.1908089953765448` 0.981627183447664`
12 0.20791169081775934` 0.9781476007338057`
13 0.224951054343865` 0.9743700647852352`
14 0.24192189559966773` 0.9702957262759965`
15 0.25881904510252074` 0.9659258262890683`
16 0.27563735581699916` 0.9612616959383189`
17 0.29237170472273677` 0.9563047559630354`
18 0.30901699437494745` 0.9510565162951535`
19 0.3255681544571567` 0.9455185755993168`
20 0.3420201433256687` 0.9396926207859084`
21 0.35836794954530027` 0.9335804264972017`
22 0.374606593415912` 0.9271838545667874`
23 0.39073112848927377` 0.9205048534524404`
24 0.4067366430758002` 0.9135454576426009`
25 0.42261826174069944` 0.9063077870366499`
26 0.4383711467890774` 0.898794046299167`
27 0.45399049973954675` 0.8910065241883679`
28 0.4694715627858908` 0.882947592858927`
29 0.48480962024633706` 0.8746197071393957`
30 0.5` 0.8660254037844386`
31 0.5150380749100542` 0.8571673007021123`
32 0.5299192642332049` 0.848048096156426`
33 0.5446390350150271` 0.838670567945424`
34 0.5591929034707469` 0.8290375725550416`
35 0.573576436351046` 0.8191520442889918`
36 0.5877852522924731` 0.8090169943749475`
37 0.6018150231520483` 0.7986355100472928`
38 0.6156614753256583` 0.7880107536067219`
39 0.6293203910498374` 0.7771459614569709`
40 0.6427876096865393` 0.766044443118978`
41 0.6560590289905073` 0.754709580222772`
42 0.6691306063588582` 0.7431448254773942`
43 0.6819983600624985` 0.7313537016191705`
44 0.6946583704589973` 0.7193398003386512`
45 0.7071067811865476` 0.7071067811865476`
46 0.7193398003386511` 0.6946583704589973`
47 0.7313537016191705` 0.6819983600624985`
48 0.7431448254773942` 0.6691306063588582`
49 0.754709580222772` 0.6560590289905073`
50 0.766044443118978` 0.6427876096865394`
51 0.7771459614569709` 0.6293203910498375`
52 0.788010753606722` 0.6156614753256583`
53 0.7986355100472928` 0.6018150231520484`
54 0.8090169943749475` 0.5877852522924731`
55 0.8191520442889918` 0.5735764363510462`
56 0.8290375725550417` 0.5591929034707468`
57 0.838670567945424` 0.5446390350150271`
58 0.848048096156426` 0.5299192642332049`
59 0.8571673007021123` 0.5150380749100542`
60 0.8660254037844386` 0.5`
61 0.8746197071393957` 0.4848096202463371`
62 0.8829475928589269` 0.46947156278589086`
63 0.8910065241883678` 0.4539904997395468`
64 0.898794046299167` 0.43837114678907746`
65 0.9063077870366499` 0.42261826174069944`
66 0.9135454576426009` 0.4067366430758002`
67 0.9205048534524404` 0.3907311284892737`
68 0.9271838545667874` 0.37460659341591196`
69 0.9335804264972017` 0.3583679495453004`
70 0.9396926207859083` 0.3420201433256688`
71 0.9455185755993167` 0.32556815445715676`
72 0.9510565162951535` 0.30901699437494745`
73 0.9563047559630354` 0.29237170472273677`
74 0.9612616959383189` 0.27563735581699916`
75 0.9659258262890683` 0.25881904510252074`
76 0.9702957262759965` 0.24192189559966767`
77 0.9743700647852352` 0.22495105434386492`
78 0.9781476007338056` 0.20791169081775945`
79 0.981627183447664` 0.19080899537654492`
80 0.984807753012208` 0.17364817766693041`
81 0.9876883405951378` 0.15643446504023092`
82 0.9902680687415704` 0.13917310096006547`
83 0.992546151641322` 0.12186934340514749`
84 0.9945218953682733` 0.10452846326765346`
85 0.9961946980917455` 0.08715574274765814`
86 0.9975640502598242` 0.06975647374412523`
87 0.9986295347545738` 0.052335956242943966`
88 0.9993908270190958` 0.03489949670250108`
89 0.9998476951563913` 0.0174524064372836`
90 1.` 0.`

•Tehtävä 3

In[9]:=

Table[k^j, {j, 1, 10}, {k, 1, 10}] // TableForm

Out[9]//TableForm=
1 2 3 4 5 6 7 8 9 10
1 4 9 16 25 36 49 64 81 100
1 8 27 64 125 216 343 512 729 1000
1 16 81 256 625 1296 2401 4096 6561 10000
1 32 243 1024 3125 7776 16807 32768 59049 100000
1 64 729 4096 15625 46656 117649 262144 531441 1000000
1 128 2187 16384 78125 279936 823543 2097152 4782969 10000000
1 256 6561 65536 390625 1679616 5764801 16777216 43046721 100000000
1 512 19683 262144 1953125 10077696 40353607 134217728 387420489 1000000000
1 1024 59049 1048576 9765625 60466176 282475249 1073741824 3486784401 10000000000

•Tehtävä 4

Syötetään annetut vektorit

In[10]:=

c = {7, 5} ;

In[11]:=

a = {3, 4} ;

In[12]:=

b = {5, -1} ;

In[13]:=

rtk = Solve[c == x a + y b , {x, y}]

Out[13]=

{{x -> 32/23, y -> 13/23}}

In[14]:=

komponentit = {x a, y b} /. First[rtk]

Out[14]=

{{96/23, 128/23}, {65/23, -13/23}}

Näiden summa on todellakin c:

In[15]:=

komponentit[[1]] + komponentit[[2]] == c

Out[15]=

True

•Tehtävä 5

Syötetään annetut kolmion kärkipisteet:

In[16]:=

a = {1, 2} ;

In[17]:=

b = {-3, 5} ;

In[18]:=

c = {-1, -6} ;

Keskijanojen leikkauspiste on probleeman tuntematon:

In[19]:=

p = {x, y}

Out[19]=

{x, y}

Ehdot, joissa r, s ja t ovat tuntemattomia skalaareja (piirrä kuvio):FormBox[Cell[], TraditionalForm]

In[20]:=

yhtalot = {p == a + r ((b + c)/2 - a), p == b + s ((c + a)/2 - b), p == c + t ((a + b)/2 - c)}

Out[20]=

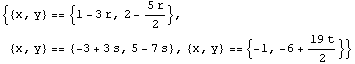
{{x, y} == {1 - 3 r, 2 - (5 r)/2}, {x, y} == {-3 + 3 s, 5 - 7 s}, {x, y} == {-1, -6 + (19 t)/2}}

Jos tällä yhtälöryhmällä on ratkaisu, vaikka siinä on kolme yhtälöä ja viisi tuntematonta,
keskijanat todellakin leikkaavat samassa pisteessä:

In[21]:=

rtk = Solve[yhtalot, {x, y, r, s, t}]

Out[21]=

{{x -> -1, y -> 1/3, r -> 2/3, s -> 2/3, t -> 2/3}}

Keskijanojen leikkauspiste:

In[22]:=

p /. First[rtk]

Out[22]=

{-1, 1/3}

Skalaarit r, s ja t ovat kaikki = 2/3, mikä osoittaa jakosuhteen.

•Tehtävä 6

Syötetään annetut avaruuden tason pisteet:

In[23]:=

a = {7, 3, 1} ;

In[24]:=

b = {1, 2, 3} ;

In[25]:=

c = {3, 5, -5} ;

Lasketaan niiden väliset vektorit. Nimet viittaavat annettuihin pisteisiin.

In[26]:=

ab = a - b

Out[26]=

{6, 1, -2}

In[27]:=

bc = b - c

Out[27]=

{-2, -3, 8}

Lasketaan pintaa vastaan oleva kohtisuora vektori ristitulolla:

In[28]:=

e = Cross[ ab, bc]

Out[28]=

{2, -44, -16}

Tehdään vektorista yksikkövektori käyttäen apuna pistetulon kaavaa:

In[29]:=

e = e / Sqrt[ e . e ]

Out[29]=

{1/(3 61^(1/2)), -22/(3 61^(1/2)), -8/(3 61^(1/2))}

•Tehtävä 7

Haetaan 20 ensimmäistä alkulukua:

In[30]:=

a = Table[ Prime[i], {i, 20} ]

Out[30]=

{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71}

Otetaan edellisen taulukon alkiot järjestysluvuiksi ja haetaan vastaavia järjestyslukuja olevat alkuluvut:

In[31]:=

b = Table[ Prime[ a[[i]] ], {i, Length[a]} ]

Out[31]=

{3, 5, 11, 17, 31, 41, 59, 67, 83, 109, 127, 157, 179, 191, 211, 241, 277, 283, 331, 353}

•Tehtävä 8

Syötetään annetut pisteet:

In[32]:=

a = {7, 3} ;

In[33]:=

b = {1, 2} ;

In[34]:=

c = {3, 5} ;

Muodostetaan vektorit

In[35]:=

ab = a - b

Out[35]=

{6, 1}

In[36]:=

cb = c - b

Out[36]=

{2, 3}

Lasketaan kulman puolittajan suuntavektori eo. vektoreiden suuntaisten yksikkövektoreiden summana. Toinen vaihtoehto saataisiin erotuksesta.

In[37]:=

d = ab/Sqrt[ab . ab] + cb/Sqrt[cb . cb]

Out[37]=

{2/13^(1/2) + 6/37^(1/2), 3/13^(1/2) + 1/37^(1/2)}

Vastaava yksikkövektori:

In[38]:=

d0 = d / Sqrt[d . d] // FullSimplify

Out[38]=

{(1/2 + 9/(2 481^(1/2)))^(1/2), (1/2 - 9/(2 481^(1/2)))^(1/2)}

Ehkä tämä on informatiivisempi numeerisena:

In[39]:=

d0 // N

Out[39]=

{0.8397513552620198`, 0.5429711422678014`}

•Tehtävä 9

Syötetään annettu suora:

In[40]:=

r0 = {1, 2, 3} ;

In[41]:=

s0 = {4, 5, 6} ;

In[42]:=

suora = {x, y, z} == r0 + t s0

Out[42]=

{x, y, z} == {1 + 4 t, 2 + 5 t, 3 + 6 t}

Annettu taso:

In[43]:=

taso = x - 2 y + 3 z - 4 == 0

Out[43]=

-4 + x - 2 y + 3 z == 0

Leikkauspiste:

In[44]:=

rtk = Solve[{suora, taso}, {x, y, z, t}]

Out[44]=

{{x -> 1/3, y -> 7/6, z -> 2, t -> -1/6}}

In[45]:=

{x, y, z} /. First[rtk]

Out[45]=

{1/3, 7/6, 2}

•Tehtävä 10

Vrt. tehtävään 5.

Syötetään annetut kolmion kärkipisteet:

In[46]:=

a = {a1, a2} ;

In[47]:=

b = {b1, b2} ;

In[48]:=

c = {c1, c2} ;

Keskijanojen leikkauspiste on probleeman tuntematon:

In[49]:=

p = {x, y}

Out[49]=

{x, y}

Ehdot, joissa r, s ja t ovat tuntemattomia skalaareja (piirrä kuvio):FormBox[Cell[], TraditionalForm]

In[50]:=

yhtalot = {p == a + r ((b + c)/2 - a), p == b + s ((c + a)/2 - b), p == c + t ((a + b)/2 - c)}

Out[50]=

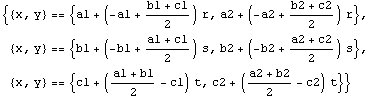
{{x, y} == {a1 + (-a1 + (b1 + c1)/2) r, a2 + (-a2 + (b2 + c2)/2) r}, {x, y} == {b1 + (-b1 + (a ... s, b2 + (-b2 + (a2 + c2)/2) s}, {x, y} == {c1 + ((a1 + b1)/2 - c1) t, c2 + ((a2 + b2)/2 - c2) t}}

Jos tällä yhtälöryhmällä on ratkaisu, vaikka siinä on kolme yhtälöä ja viisi tuntematonta,
keskijanat todellakin leikkaavat samassa pisteessä:

In[51]:=

rtk = Solve[yhtalot, {x, y, r, s, t}]

Out[51]=

{{y -> 1/3 (a2 + b2 + c2), r -> 2/3, s -> 2/3, x -> 1/3 (a1 + b1 + c1), t -> 2/3}}

Keskijanojen leikkauspiste:

In[52]:=

p /. First[rtk]

Out[52]=

{1/3 (a1 + b1 + c1), 1/3 (a2 + b2 + c2)}

Skalaarit r, s ja t ovat kaikki = 2/3, mikä osoittaa jakosuhteen.

Converted by Mathematica  (August 20, 2003)